UNITÀ 2
La rappresentazione
delle leggi fisiche
Conoscenze
•
Conoscere diversi tipi di proporzionalità
Abilità
•
•
Rappresentare leggi fisiche in quanto relazioni matematiche
Ricavare formule inverse
1
1 Proporzioni e percentuali
Una proporzione è un’uguaglianza tra due rapporti
Proprietà delle proporzioni
In una proporzione qualunque a : b = c : d
i termini a e d sono chiamati estremi
i termini b e c sono chiamati medi
2
1 Proporzioni e percentuali
Per qualunque proporzione valgono le seguenti proprietà
il prodotto dei medi è uguale al prodotto degli estremi
a·d=b·c
un estremo è uguale al prodotto dei medi diviso l’altro
estremo
un medio è uguale al prodotto degli estremi diviso l’altro
medio
3
1 Proporzioni e percentuali
Percentuale Una percentuale equivale a una frazione con
denominatore uguale a 100
Calcolo delle percentuali
P : 100 = N: T
dove
P è la percentuale
N è la quantità corrispondente alla percentuale
T è il totale
4
2 Tabelle e grafici cartesiani
Tabelle
Una tabella a due colonne permette di presentare
ordinatamente i valori di due grandezze
5
2 Tabelle e grafici cartesiani
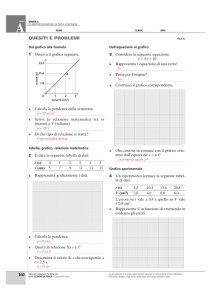
Grafici cartesiani
Un grafico o diagramma cartesiano per punti
è formato da due assi perpendicolari che si incontrano
in un punto chiamato origine
– asse delle ascisse (o asse x)
– asse delle ordinate (o asse y)
Fissata un’unità di misura sui due assi
i numeri che indicano le distanze di ogni punto del piano
dagli assi sono le sue coordinate cartesiane
– ascissa
– ordinata
• l’asse delle ascisse e quello delle ordinate sono
anche detti assi cartesiani
6
2 Tabelle e grafici cartesiani
7
2 Tabelle e grafici cartesiani
8
2 Tabelle e grafici cartesiani
Grafici sperimentali
In un grafico sperimentale è necessario riportare
i valori delle misure delle due grandezze x e y
i rispettivi errori assoluti
– il grafico sarà composto da rettangoli dove
• il centro rappresenta la misura attendibile
• le dimensioni rappresentano il doppio degli
errori assoluti delle misure delle due grandezze
9
2 Tabelle e grafici cartesiani
10
2 Tabelle e grafici cartesiani
Interpolazione ed estrapolazione
Dato un grafico cartesiano è possibile
ricavare altri valori delle grandezze rappresentate, in
aggiunta a quelli utilizzati per tracciare il grafico stesso
– interpolazione
prolungare il grafico oltre i valori forniti nella tabella
deducendo ulteriori dati
– estrapolazione
11
3 Le funzioni matematiche
Le funzioni matematiche sono un modo per esprimere la relazione
fra due grandezze fisiche che descrivono un fenomeno
Funzione matematica y = f(x)
Una variabile y è funzione di un’altra variabile x se a ogni valore della
variabile x corrisponde un unico valore della variabile y. La variabile x si
dice variabile indipendente, la variabile y si dice variabile
dipendente, perché i suoi valori dipendono da quelli assegnati alla
variabile x
Una funzione matematica può essere rappresentata con
una formula matematica
una tabella
un grafico cartesiano
12
4 La relazione di proporzionalità diretta
Due grandezze sono direttamente proporzionali se il loro
rapporto si mantiene costante
L’espressione algebrica della relazione è
Relazione di
proporzionalità diretta
Nella relazione di proporzionalità diretta y = kx, il valore della
costante k determina la pendenza della semiretta
corrispondente sul grafico cartesiano. Maggiore è il valore di
k, maggiore è la pendenza della semiretta e quindi maggiore
è l’angolo che la semiretta forma con l’asse x. Il coefficiente k
è detto anche coefficiente angolare della retta
13
4 La relazione di proporzionalità diretta
esempio supponiamo di comprare del pane
che costa 1,5€ al Kg costruiamo tabella e
grafico corrispondente
L’espressione matematica si ottiene trovando k il prezzo al kg
Quindi K= 1,5 da cui y=1,5x
14
5 La relazione lineare
Si dicono funzioni lineari tutte le funzioni che hanno per
grafico una retta e che sono espresse dalla relazione
y = mx + q
m è il coefficiente angolare
– determina la pendenza della retta
– rappresenta il rapporto fra la differenza delle
coordinate di due punti qualsiasi della retta
q è il termine noto e rappresenta il punto di
intersezione della retta con l’asse y
15
5 La relazione lineare
16
6 La relazione di proporzionalità inversa
Due grandezze sono inversamente proporzionali se il loro
prodotto si mantiene costante
L’espressione algebrica della relazione è
Relazione di
proporzionalità inversa
La curva che rappresenta la relazione di proporzionalità
inversa è un ramo di iperbole
17
6 La relazione di proporzionalità inversa
18
6 La relazione di proporzionalità inversa
Il volume è costante k e si ottiene moltiplicando A*h quindi K=400
yx=400
y=400/x h=400/A
19
7 La relazione di proporzionalità
quadratica
In una relazione di proporzionalità quadratica
le variabili sono correlate da una funzione di
secondo grado
– il grafico è una parabola
Due grandezze sono direttamente proporzionali al
quadrato se è costante il rapporto tra i valori della
grandezza y (variabile dipendente) e i quadrati dei
corrispondenti valori della grandezza x (variabile
indipendente)
In simboli
Relazione di
proporzionalità quadratica
20
7 La relazione di proporzionalità
quadratica
Esempio
21
8 Risolvere equazioni
Ricavare formule inverse
Nelle equazioni di molte leggi fisiche compaiono più grandezze
espresse da lettere
per isolare una qualunque di queste grandezze è
necessario ricavare la formula inversa
– si applicano i due principi di equivalenza
22
Altre formule inverse
F=ma
a= F/m
m=F/a
23