SERVOMOTORI IN CORRENTE CONTINUA
CON A ECCITAZIONE A M.P.
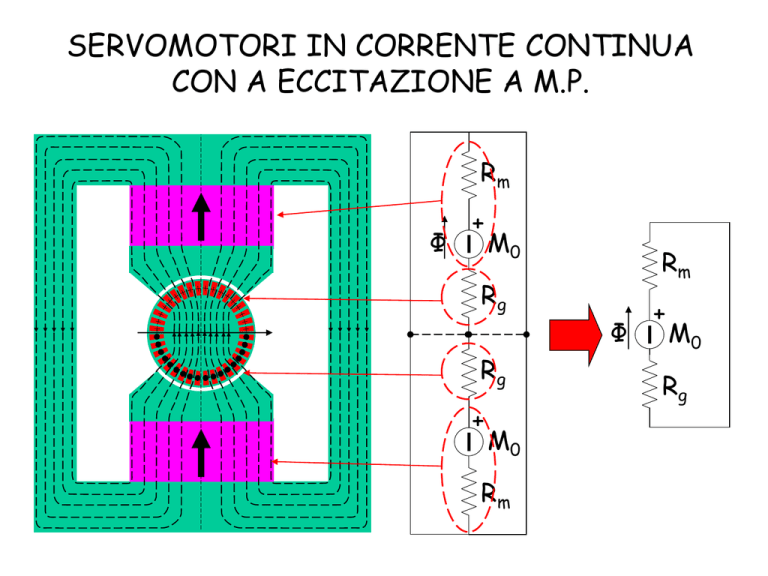
Rm
Φ
+
M0
Rg
Rg
+
M0
Rm
Rm
Φ
+
M0
Rg
rotore
(avv. armatura)
spazzola
collettore
spazzola
carcassa
ferromagnetica
statore
(M.P. di eccitazione)
CONFIGURAZIONE TIPICA
DELL’AVVOLGIMENTO DI INDOTTO
a regime =0
EQUAZIONI DEL MOTORE IN CC
ECCITAZIONE INDIPENDENTE
dIa
V KΦΩ RaIa L
eq. elettrica
dt
dΩ
eq. meccanica
C CL Cp J
dt
ricavo Ia
Ia
V KΦΩ
Ra
V KΦΩ
Ω caratteristica meccanica
C KΦIa KΦ
Cs (1
)
Ra
Ω0
V
Ω0
KΦ
V
Cs KΦ
Ra
velocità a vuoto
coppia di spunto
C
Cs
V crescente
0
Allo spunto Ia= Is=V/Ra= Ia,nV/(RaIa,n) (Ia,n: valore nominale di Ia)
Poiché la caduta di tensione RaIa,nom è di solito di qualche %, si ha
che Is è dell’ordine delle decine di volte di Ia,nom; riportando quindi
sull’asse delle ordinate valori di coppia corrispondenti a quella
nominale Cn=kΦInom si ha che, essendo la coppia di spunto Cs delle
decine di volte di Cn, la caratteristica meccanica è quasi verticale, e
dunque la velocità del motore varia di poco da vuoto a carico.
C
Cn
V crescente
Cr
Ω0
Ω
CIRCUITO EQUIVALENTE 1
R
I
E
V
non tiene conto di altre perdite
oltre a quelle ohmiche
V E RI VI Pe EI RI2
potenza elettrica convertita in meccanica
CIRCUITO EQUIVALENTE 2
R
V
I
2
E2
2 E
VI EI RI Pp
RI
RL
Rh
2
La potenza meccanica EI può essere
E
Rh
RL considerata in un circuito equivalente come la
potenza assorbita da una resistenza variabile
RL, mentre le perdite nel ferro vengono
tenute in conto con una resistenza Rh.
Le perdite nel ferro per isteresi sono proporzionali, a parità di induzione
e quindi di flusso, alla frequenza f e quindi ad Ω ovvero ad E, mentre le
perdite per correnti parassite sono proporzionali a f2 e ad E2; assumendo
una Rh costante si ottengono perdite nel ferro proporzionali a E2 e quindi
ciò equivale a considerarle come dovute solo a correnti parassite.
MOTORI CON MAGNETI IN ALNICO
espansione polare
carcassa
(amagnetica)
gioghi ferromagnetici
espansione polare
MOTORI CON MAGNETI IN FERRITE
giogo ferromagnetico
magnete anulare
magnetizzazione anisotropa
espansioni polari a
“coda di colomba”
magnete a “coda di colomba” (dovetail)
magnetizzazione anisotropa
magnete espansione
permanente
polare
espansione magnete
polare permanente
MOTORE CON
M.P. A TERRE RARE
(magneti larghi e corti)
MOTORI CON
M.P. IN ALNICO
(magneti stretti e lunghi)
ACCORGIMENTO PER INCREMENTARE IL
FLUSSO CON MAGNETI IN FERRITE
EFFETTO DELLA REAZIONE DI INDOTTO
S
S
S
N
N
N
LINEE DI FLUSSO LINEE DI FLUSSO LINEE DI FLUSSO A
SOLO CON M.P. SOLO CON LA FMM
CARICO
DI ARMATURA
in queste zone l’effetto smagnetizzante
della fmm di armatura può portare il M.P.
oltre il ginocchio
ACCORGIMENTI PER RIDURRE L’EFFETTO
DELLA REAZIONE DI INDOTTO
M.P.
espansioni
ferromagnetiche
(cortocircuitano
magneticamente il
campo di armatura
che quindi non
smagnetizza i MP)
M.P.
il traferro è
aumentato dove la
fmm di armatura è
più intensa
T BNIlR BlπR NI
1
1
Φ As
π
π
Con M.P. con Br più elevata e Hc più
bassa (AlNiCo) posso pensare di
avere flusso più elevato e meno As,
quindi denti di rotore più larghi e
cave più strette (IRON MACHINE)
Al contrario, con le ferriti (Br
bassa, Hc più elevata) privilegio As
rispetto al flusso denti di rotore
più stretti e cave più larghe
(COPPER MACHINE)
indotto tipo “slotless” (senza cave)
Per abbassare il momento di inerzia
conviene, dove possibile, piazzare i
conduttori verso il fondo cava (NB:
JMR2)
indotto tipo “moving coil” (la parte
ferromagnetica di rotore in azzurro è
fissa)
fibra di vetro
VISTA ESPLOSA DI MOTORE CON INDOTTO TIPO “MOVING COIL”
VISTA D’ASSIEME DI UN TIPICO MOTORE “MOVING COIL” CON CAMPO
DI ECCITAZIONE ESTERNO
carcassa in acciaio
dolce (magnetico)
albero in acciaio
inossidabile
cuscinetto
terminale di
alimentazione
rotore con indotto
“moving-coil”
magnete permanente
VISTA ESPLOSA DI MOTORE CON CAMPO DI ECCITAZIONE INTERNO
(“CORELESS”) ED INDOTTO TIPO “FAULHABER”
magnete permanente interno (fisso)
indotto con avvolgimento “moving-coil” tipo
“FAULHABER”
carcassa in materiale ferromagnetico
terminali di alimentazione
costruzione di un avvolgimento
tipo “FAULHABER”
costruzione di un avvolgimento tipo “rombico”
ALTRI TIPI DI AVVOLGIMENTI PER MOTORI “CORELESS”
rotore con indotto di tipo “rombico”
indotto di tipo “a campana” (tratteggiato il
riempimento in resina)
vista sezionata di rotore con indotto “a palla”
supporto in
magneti
materiale plastico
avvolgimento
rotore con indotto “a palla”
VISTA ESPLOSA DI MOTORE A TRAFERRO PIANO (FLUSSO ASSIALE)
DEL TIPO “PANCAKE” (letteralmente “FRITTELLA”)
giogo in acciaio dolce
magneti
particolare delle bobine
dell’avvolgimento
avvolgimento di armatura
collettore
giogo in acciaio dolce
rotore
motore
assemblato
VISTA ESPLOSA DI MOTORE A TRAFERRO PIANO (FLUSSO ASSIALE)
DEL TIPO “PRINTED”
magneti in AlNiCo
magneti in ferrite
spazzole
rappresentazione di alcune
spire
MOTORE A DISCO “A 3 BOBINE”
avvolgimento rotorico
rappresentazione rettificata (3 bobine,
4 poli, 6 spazzole; notare i collegamenti,
sono attive 2 bobine su 3, in quanto la
terza vede fem uguali ed opposte sui
due lati)
Motori con cave
Manufacturers
UCJMED
-10M
Item
Inertia J
Electrical time constant E
Mechanical time constant M
Torque constant KT
Back-e.m.f. constant KE
Armature resistance Ra
Power rate
Rated continuous torque T
Rated rotational speed
Rated output P0
Rated voltage
Weight
10-6 kg m 2
ms
ms
600.
6.
13.7
47.
47.
5.
1.5
0.95
1000.
100.
64.
6.
10-2NmA-1
10-2V s rad-1
kWs-1
Nm
r.p.m.
W
V
kg
Yasukawa Electric Mfg. Co. Ltd.
UCJMED
UGJMED
UGTMEM
UGTMEM
UGTMEM
-40L
-01SB4
-03MB2
-06SB2
1600.
2000.
1.57
23.5
95.
12.2
10.1
0.3
0.8
1.9
24.8
28.5
4.1
6.5
11.7
37.
50.6
3.4
7.5
9.3
37.
50.6
3.4
7.5
9.3
1.05
1.3
3.2
1.59
1.02
1.5
29.
1.5
2.4
1.6
1.53
2.4
0.05
0.24
0.39
1000.
1000.
3000.
2000.
1300.
160.
250.
15.
50.
53.
44.
60.
20.3
24.4
19.8
10.5
12.
0.22
1.1
1.6
Tamagawa Seiki Co . Ltd.
TS908N TS908N8 TS688N6 TS902N2 TS668N4
-E4
-E3
-E3
-E6
E6
0.92
1.57
2.5
28.4
39.2
0.45
0.3
0.8
1.6
1.3
9.
7.
8.
12.
12.
3.82
3.92
3.72
6.43
6.47
3.82
3.92
3.72
6.43
6.47
14.3
6.9
4.
1.7
1.3
0.2
0.71
0.35
0.87
1.92
0.14
0.33
0.29
1.57
1.96
3750.
3000.
3300.
4000.
4000.
5.
10.
10.
60.
80.
21.
21.
18.3
30.8
31.3
0.09
0.15
0.4
1.3
1.5
Motori slotless
Manufacturers
Item
Inertia J
Electrical time constant E
2
10-6 kgm
ms
Mechanical time constant M
Torque constant KT
ms
Back-e.m.f. constant KE
10 Vs rad
Armature resistance Ra
Power rate
Rated continuous torque T
Rated rotational speed
Rated output P0
Rated voltage
-2
10 NmA
-2
-1
-1
kWs
-1
-1
10 Nm
r.p.m.
W
V
Yasukawa Electric Mfg. Co. Ltd.
Olympus Opto Electronic Co. Ltd.
UGMMEM
-06AA1
56.7
UGMMEM
-13AA141.
UGMMEM
-25AA1
283.
OMS-312
0.13
1.1
1.5
1.3
0.09
0.11
0.2
0.28
4.7
10.
4.6
17.8
0.6
19.3
10.
0.85
10.
0.89
9.5
2.3
9.5
2.1
OMS-512
OMS-1024 OMS-2024
0.22
0.58
1.73
10.
17.8
19.3
0.85
0.89
2.3
2.3
0.84
6.1
1.03
11.5
0.47
21.5
5.3
0.07
3.6
0.11
6.3
0.29
2.6
0.36
5.9
13.
25.
0.03
0.05
0.13
0.25
3000.
185.
40.5
3000.
401.
68.5
3000.
771.
70.9
10500.
3.
12.
10500.
5.
12.
9200.
10.
24.
9200.
20.
24.
Motori moving-coil
Sanyo Denki Co., Ltd.
H1008 -101
H1009 -101
H1420 -102
Manufacturers and models
Inertia J
Electrical time constant E
Mechanical time constant M
Torque constant K T
Back-e.m.f. constant K E
Armature resistance Ra
Power rate
Rated continuous torque T
Rated speed O
Rated output power P O
10-6 kg m 2
ms
ms
4.9
0.17
2.3
4.11
4.11
0.7
6.5
0.18
4500.
85.
10-2NmA-1
10-2 V s rad-1
W
kWs-1
Nm
r.p.m.
W
3.5
0.14
1.5
4.5
4.5
0.55
20.
0.27
3200.
90.
76.5
0.3
2.5
13.3
13.3
0.7
22.
1.32
1120.
150.
Cylindrical rotor, outside field
Cylindrical rotor, inside field
Tamagawa Seiki Co., Ltd.
Manufacturers and models
M-1600
-A
Inertia J (10-6kgm 2)
Electrical time constant E (ms)
Mechanical time constant M (ms)
Torque constant KT (10-2Nm A-1)
Back-e.m.f. constant KE (10-2 Vsrad-1)
Armature resistance Ra ( )
Power rate (kWs-1)
Rated continuous torque T (10-1Nm)
Rated rotational speed (r.p.m.)
Rated output P 0 (W)
M-1020
-A
2.2
0.1
0.5
6.7
6.7
0.8
280.
8.5
4500.
375.
Namiki Precision
TS3516
-E17
3.3
0.12
3.8
2.54
2.54
0.7
12.3
3.3
4000.
130.
Yasukawa Electric Mfg. Co., Ltd.
UGSMEM - UGSMEM - UGSMEM - UGSMEM 02A
02B
03A
12B
4.
4.
3.3
4.65
0.16
0.14
0.15
0.16
2.
2.
1.1
0.75
4.1
8.19
4.49
6.39
4.1
8.19
4.49
6.39
0.8
3.4
0.68
0.67
11.1
11.1
34.5
28.8
0.21
0.21
0.28
0.36
3000.
3000.
4000.
3000.
43.
44.
120.
114.
TS3513
-E5
28.
0.4
1.3
16.
16.4
1.23
40.8
10.8
2100.
200.
12-2006
12-3006
2.75
0.0039
0.016
0.12
0.008
0.005
3.2
3.5
5.8
5.41
0.69
1.12
5.41
0.69
0.41
3.2
39.
46.
5.9 —
—
1.27 S0.0012
S0.0028
3850. N10000
N10000
50.
0.23
0.53
S: Starting torque
N: No-load speed
Rotor: Faulhaber winding
Seiki Co.Ltd.
16-2004
0.022
0.007
13.9
0.29
0.29
6.
—
S0.020
N12600
0.48
16-2501
0.043
0.12
6.6
0.29
2.02
63.
—
S0.038
N5600
0.4
Printed rotor
Yasukawa Electric
Mfg. Co., Ltd.
UGPMEN UGPMEE
-90DAB
-09B12
43.
34.
0.043
0.06
8.
37.
5.
3.2
5.
3.2
0.46
1.02
1.3
0.15
2.38
0.72
4000.
4000.
100.
30.
Alnico
Ferrite
magnet magnet
DINAMICA DEI SERVOMOTORI IN C.C.
di
V Ra i La
KE Ω in unità S.I. KE KT KΦ
dt
K i T J dΩ
T
c
dt
Ipotesi semplificativa preliminare: transitorio elettrico con evoluzione
molto più rapida di quella meccanica è possibile disaccoppiare lo studio
dei due fenomeni
TRANSITORIO ELETTRICO: risposta al gradino di tensione con
velocità iniziale nulla nelle ipotesi fatte, Ω=0 fintantochè non si è
giunti a regime elettrico.
V Ra i La
di
V
t/τE
i
1e
dt
Ra
V
Ra
i
La
Ra
con τ
La
E
Ra
t
TRANSITORIO MECCANICO: evoluzione della velocità a vuoto
nelle ipotesi fatte, la corrente ha il valore a regime (V-KEΩ)/Ra
KT
V -KEΩ J dΩ Ω V 1 e t/ τM
Ra
dt
KE
Ω0
Note:
V
KE
con τ
M
JRa
KEKT
Ω
τM
t
•i risultati trovati partono dal presupposto di poter disaccoppiare i due fenomeni,
cioè che τE<<τM
•la costante di tempo elettrica τE regola i transitori elettrici anche se la
macchina non è ferma: basta infatti sostituire nell’equazione elettrica al termine
noto V quello V-KEΩ; ciò consente quindi di valutare ad es. l’evoluzione della
corrente quando il motore è alimentato da un chopper
•la costante di tempo meccanica dipende, oltre che dal momento d’inerzia, anche
dalla resistenza d’armatura e dalla costante di coppia/fem; non è quindi detto
che un momento d’inerzia più elevato implichi una prestazione dinamica peggiore
•quando il motore viene accoppiato ad un carico va considerato il momento di
inerzia complessivo
TRANSITORIO COMPLETO: deriviamo l’equazione meccanica a vuoto
e sostituiamo le espressioni di i e di/dt nell’equazione meccanica
dΩ
KTi J
dt
eq. caratteris tica
di
d2Ω
J
LaJ 2 RaJ
KT
2
λ
λ KE 0
dt
dt
KT
KT
2
R
J
L
J
dΩ
d
Ω
V a
a
KE Ω
KT dt KT dt2
LaJ 2 RaJ
R
R K K
1
1
λ
λ KE 0 λ2 a λ a E T λ2 λ
0
KT
KT
La
La RaJ
τE
τE τM
radici dell'eq. caratteris tica :
4τ
1
1 1
4
1 1 1
λ1,2
1 E
2τE 2 τ2 τE τM
τE 2 2
τM
E
se τE τM
VERIFICA
le analisi disaccoppiate
approssimano bene la
soluzione esatta se τE<<τM
1
1
1
τE
1 1 1 2τE τE τM
λ1,2
1
τE 2 2
τM 1
τM
Ωm,Tm,Jm
Ωm
Ωc
Tc
ηTmΩm TcΩc
ρη
Tm
Ωc,Tc,Jc ρ: rapporto del riduttore
η: rendimento del riduttore
Ωm,Tm,Jm
CARICO EQUIVALENTE
RIPORTATO ALL’ALBERO MOTORE
riporto del momento d’inerzia
J’c
del carico a monte del riduttore
2
Ωc
Jc
1
2 1
2
JcΩc J'c Ωm J'c Jc
2
2
ρ2
Ωm
OTTIMIZZAZIONE DEL RAPPORTO DEL RIDUTTORE
IN RELAZIONE ALLE PRESTAZIONI DINAMICHE
TC
Jc dΩc TC
1
Tm
Jm
ρ
Jc γc Jm γcρ
ηρ
η
ρ
ρ2 dt
=γc: accelerazione richiesta dall’applicazione
PROBLEMA: trovare il rapporto ρmin ottimale per minimizzare la
coppia Tm soddisfacendo la specifica su γc
Tm
TC
1
Jc γc
Jm γc 0 ρmin
2
ρ
η
ρ
TC
Tmin 2
Jc γc Jm γc
η
Caso particolare: funzionamento inerziale (Tc=0)
ρmin
Jc
Jm
Tmin 2γc JcJm
TC
Jc γc
η
Jm γc
POTENZA TRANSITORIA (POWER RATE) Ps
dPm
dt
[W/s]
considerando un funzionamento con sola coppia inerziale Pm=TpeakΩm
Tpeak=JmdΩm/dt , si ha:
Ps
con
2
Tpeak
dPm
dΩm
Tpeak
dt
dt
Jm
Ottimizzando il rapporto del riduttore e cercando di ottenere la minima coppia
di picco Tpeak=Tmin che garantisce le prestazioni dinamiche richieste si trova il
minimo power rate richiesto:
2
Tmin
T
Psmin
4 c Jc γc γc
Jm
η
•NOTA 1: si osservi che Psmin dipende solo dalle caratteristiche del carico, del
riduttore e dalle prestazioni dinamiche richieste; in questo senso è utile perché
consente una verifica immediata dell’idoneità o meno del motore all’applicazione,
in quanto il power rate è un dato fornito dal costruttore del motore
•NOTA 2: non bisogna dimenticare, oltre alle prestazioni dinamiche, anche le
specifiche in termini di funzionamento a regime. Se sono state definite potenza PLn e
velocità ΩLn nominali del carico, queste vincolano Pm e Ωm/ρ: il motore ovviamente
dovrà avere una potenza nominale Pm≥PLn/η e, nota la velocità Ωm, si dovrà in generale
scegliere un rapporto ρ≠ρmin per ottenere la velocità di regime richiesta. Per quanto
possibile, si cercherà di optare per un motore che consenta di soddisfare il vincolo
sulla velocità nominale del carico con un rapporto il più vicino possibile a quello
ottimale.












