Nessun titolo diapositiva

SCUOTIMENTO DEL TERRENO - Accelerogramma
0.45
0.4
0.35
0.3
0.25
A cceleration [g]
0.2
0.15
0.1
0.05
0
- 0.05
- 0.1
- 0.15
- 0.2
- 0.25
- 0.3
0
1
2
3
4
5
6
7
8
9
10
11
Time [s ec]
12
13
14
15
16
17
18
19
20
SCUOTIMENTO DEL TERRENO – Onde Sismiche
SCUOTIMENTO DEL TERRENO – Onde Sismiche
Onde di profondità
Onde di superficie
Onde di Rayleigh
Onde P
Onde S
Onde di Love
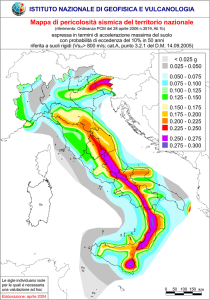
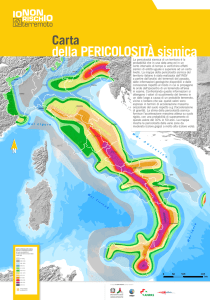
MAPPA SISMICA
1984
1a Categoria
2a Categoria
3a Categoria
Non sismica
MAPPA SISMICA
2003
MAPPE SISMICHE
Mappa Sismica 2008 – Reticolo di riferimento
NORME TECNICHE PER LE COSTRUZIONI
Mappa Sismica 2008 – Reticolo di riferimento
NORME TECNICHE PER LE COSTRUZIONI
Mappa Sismica 2008 – Reticolo di riferimento
MAPPA SISMICA INTERATTIVA INGV
Reticolo di riferimento (distanza nodi 10 km)
CRITERI GENERALI DI PROGETTAZIONE (D.M. 2008)
In ragione della necessità che la costruzione sia dotata di sistemi strutturali capaci, con costi
accettabili, di soddisfare i requisiti di sicurezza nei confronti sia dei carichi verticali che dell’azione
sismica, in siti a sismicità significativa i criteri di progettazione nei confronti delle azioni sismiche devono
essere considerati già nell’impostazione della progettazione strutturale.
La costruzione deve essere dunque dotata di sistemi resistenti lungo almeno due direzioni e capaci di
garantire un’adeguata resistenza e rigidezza nei confronti sia dei moti traslazionari, sia dei moti
torsionali dovuti all’eccentricità tra il centro di massa ed il centro di rigidezza dell’intera struttura o anche
solo di una sua porzione.
Tali moti torsionali tendono a sollecitare i diversi elementi strutturali in maniera non uniforme. A tal fine,
sono da preferirsi configurazioni strutturali in cui i principali elementi resistenti all’azione sismica
sono distribuiti nelle zone periferiche della costruzione e al contempo limitano l’eccentricità tra
centro di massa e centro di rigidezza a ciascun livello della costruzione. Per massimizzare la rigidezza
torsionale conseguita nel modo suddetto è necessario che gli orizzontamenti funzionino da diaframma
rigido ai fini della ripartizioni delle forze sugli elementi verticali che li sostengono, nei modi specificati al
Cap. 7.2.6 delle Norme Tecniche per le Costruzioni.
CRITERI GENERALI DI PROGETTAZIONE (D.M. 2008)
In ragione della necessità che la costruzione sia dotata di sistemi strutturali capaci, con costi
accettabili, di soddisfare i requisiti di sicurezza nei confronti sia dei carichi verticali che dell’azione
sismica, in siti a sismicità significativa i criteri di progettazione nei confronti delle azioni sismiche devono
essere considerati già nell’impostazione della progettazione strutturale.
La costruzione deve essere dunque dotata di sistemi resistenti lungo almeno due direzioni e capaci di garantire un’adeguata resistenza e
rigidezza nei confronti sia dei moti traslazionari, sia dei moti torsionali dovuti all’eccentricità tra il centro di massa ed il centro di rigidezza
dell’intera struttura o anche solo di una sua porzione.
Tali moti torsionali tendono a sollecitare i diversi elementi strutturali in maniera non uniforme. A tal fine, sono da preferirsi configurazioni
strutturali in cui i principali elementi resistenti all’azione sismica sono distribuiti nelle zone periferiche della costruzione e al contempo
limitano l’eccentricità tra centro di massa e centro di rigidezza a ciascun livello della costruzione. Per massimizzare la rigidezza torsionale
conseguita nel modo suddetto è necessario che gli orizzontamenti funzionino da diaframma rigido ai fini della ripartizioni delle forze sugli elementi
verticali che li sostengono, nei modi specificati al Cap. 7.2.6 delle Norme Tecniche per le Costruzioni.
MODELLAZIONE STRUTTURALE
Schema ERRATO – Plinti non collegati
MODELLAZIONE STRUTTURALE
Schema CORRETTO – Plinti collegati
CRITERI GENERALI DI PROGETTAZIONE (D.M. 2008)
In ragione della necessità che la costruzione sia dotata di sistemi strutturali capaci, con costi accettabili, di soddisfare i requisiti di sicurezza nei
confronti sia dei carichi verticali che dell’azione sismica, in siti a sismicità significativa i criteri di progettazione nei confronti delle azioni sismiche
devono essere considerati già nell’impostazione della progettazione strutturale.
La costruzione deve essere dunque dotata di sistemi resistenti lungo almeno due direzioni e capaci di
garantire un’adeguata resistenza e rigidezza nei confronti sia dei moti traslazionari, sia dei moti
torsionali dovuti all’eccentricità tra il centro di massa ed il centro di rigidezza dell’intera struttura o anche
solo di una sua porzione.
Tali moti torsionali tendono a sollecitare i diversi elementi strutturali in maniera non uniforme. A tal fine, sono da preferirsi configurazioni
strutturali in cui i principali elementi resistenti all’azione sismica sono distribuiti nelle zone periferiche della costruzione e al contempo
limitano l’eccentricità tra centro di massa e centro di rigidezza a ciascun livello della costruzione. Per massimizzare la rigidezza torsionale
conseguita nel modo suddetto è necessario che gli orizzontamenti funzionino da diaframma rigido ai fini della ripartizioni delle forze sugli elementi
verticali che li sostengono, nei modi specificati al Cap. 7.2.6 delle Norme Tecniche per le Costruzioni.
MODELLAZIONE STRUTTURALE
MODELLAZIONE STRUTTURALE
MODELLAZIONE STRUTTURALE
MODELLAZIONE STRUTTURALE
ANALISI SISMICA DELLE STRUTTURE
Baricentro delle Masse e delle Rigidezze
ANALISI SISMICA DELLE STRUTTURE
Baricentro delle Masse e delle Rigidezze
Struttura 1
Struttura 2
ANALISI SISMICA DELLE STRUTTURE
Baricentro delle Masse e delle Rigidezze
Struttura 1
Struttura 2
ANALISI SISMICA DELLE STRUTTURE
Posizione del Baricentro delle Rigidezze
s  u 0    yi , xi 
Spostamento globale del singolo
elemento
ui  u0 x    yi
vi  u0 y    xi
Traslazione e rotazione dell’impalcato rigido
Componenti dello spostamento globale
ANALISI SISMICA DELLE STRUTTURE
Posizione del Baricentro delle Rigidezze
K ix 
12  E  I x
h3
K iy 
12  E  I y
h3
Rigidezza del singolo elemento
Fxi  Ki u0 x    yi   Kix  u0 x    K xi  yi
Fyi  K i u0 y    xi   K iy  u0 y    K yi  yi
Aliquota della forza tagliante di piano che sopporta il singolo elemento
FxT   Kix  u0 x     Kix  yi
FyT   Kiy  u0 y     Kiy  xi
Forza tagliante di piano totale
ANALISI SISMICA DELLE STRUTTURE
Posizione del Baricentro delle Rigidezze
YR
K y


K
xi
i
xi
XR
K x


K
yi
i
yi
Coordinate del baricentro delle rigidezze dell’impalcato
ANALISI SISMICA DELLE STRUTTURE
Posizione del Baricentro delle Rigidezze
ANALISI SISMICA DELLE STRUTTURE
Posizione del Baricentro delle Rigidezze
ANALISI SISMICA DELLE STRUTTURE
Posizione del Baricentro delle Rigidezze
ANALISI SISMICA DELLE STRUTTURE
Posizione del Baricentro delle Rigidezze
CRITERI GENERALI DI PROGETTAZIONE (D.M. 2008)
In ragione della necessità che la costruzione sia dotata di sistemi strutturali capaci, con costi accettabili, di soddisfare i requisiti di sicurezza nei
confronti sia dei carichi verticali che dell’azione sismica, in siti a sismicità significativa i criteri di progettazione nei confronti delle azioni sismiche
devono essere considerati già nell’impostazione della progettazione strutturale.
La costruzione deve essere dunque dotata di sistemi resistenti lungo almeno due direzioni e capaci di garantire un’adeguata resistenza e
rigidezza nei confronti sia dei moti traslazionari, sia dei moti torsionali dovuti all’eccentricità tra il centro di massa ed il centro di rigidezza
dell’intera struttura o anche solo di una sua porzione.
Tali moti torsionali tendono a sollecitare i diversi elementi strutturali in maniera non uniforme. A tal fine,
sono da preferirsi configurazioni strutturali in cui i principali elementi resistenti all’azione sismica
sono distribuiti nelle zone periferiche della costruzione e al contempo limitano l’eccentricità tra
centro di massa e centro di rigidezza a ciascun livello della costruzione. Per massimizzare la rigidezza
torsionale conseguita nel modo suddetto è necessario che gli orizzontamenti funzionino da diaframma
rigido ai fini della ripartizioni delle forze sugli elementi verticali che li sostengono, nei modi specificati al
Cap. 7.2.6 delle Norme Tecniche per le Costruzioni.
ANALISI SISMICA DELLE STRUTTURE
Distribuzione degli elementi sismo-resistenti
ANALISI SISMICA DELLE STRUTTURE
Distribuzione degli elementi sismo-resistenti
Doppia rottura diagonale per taglio su un nucleo in c.a..
CORREZIONE TORSIONALE
VECCHIA NORMA - D.M. ‘96
A/B > 2.5
Analisi Sismica Statica
CORREZIONE TORSIONALE
Metodo dell’incremento dell’eccentricità (5% di “d”)
.
CORREZIONE TORSIONALE
Metodo del coefficiente
d
d  1  0.6  x / Lc
Per edifici aventi massa e rigidezza distribuite in modo simmetrico in pianta.
MODELLAZIONE STRUTTURALE
1 – Sbalzi
2 – Pilastri in falso
3 – Luci elevate
4 – Travi a spessore
Modellazioni sconsigliate
ANALISI SISMICA DELLE STRUTTURE
Ipotesi Fondamentali:
- Nella pratica professionale non è necessario conoscere l’andamento nel tempo delle
caratteristiche di sollecitazione in ogni sezione dell’elemento strutturale, ma è sufficiente
conoscerne il valore massimo.
- Nelle strutture tipiche dell’ingegneria civile (ad esempio edifici per civile abitazione) le masse
strutturali sono concentrate in massima parte in corrispondenza degli impalcati (solai).
- In alcuni casi (edifici in c.a.) gli impalcati possono essere considerati elementi indeformabili
nel proprio piano, e quindi in grado di connettere rigidamente tutti i nodi strutturali giacenti su
di essi.
ANALISI SISMICA DELLE STRUTTURE
Ipotesi Fondamentali:
- Nella pratica professionale non è necessario conoscere l’andamento nel tempo delle
caratteristiche di sollecitazione in ogni sezione dell’elemento strutturale, ma è sufficiente
conoscerne il valore massimo.
- Nelle strutture tipiche dell’ingegneria civile (ad esempio edifici per civile abitazione) le masse strutturali sono concentrate in
massima parte in corrispondenza degli impalcati (solai).
- In alcuni casi (edifici in c.a.) gli impalcati possono essere considerati elementi indeformabili nel proprio piano, e quindi in grado
di connettere rigidamente tutti i nodi strutturali giacenti su di essi.
L’EFFETTO DEL SISMA SULLE STRUTTURE
le azioni dinamiche agenti nella struttura dovute all’accelerazione delle masse
F (t )  m  a(t )  var iabile
vengono sostituite da azioni statiche equivalenti
F  cos t
0.45
0.4
0.35
0.3
0.25
A cceleration [g]
0.2
0.15
0.1
0.05
0
- 0.05
- 0.1
- 0.15
- 0.2
- 0.25
- 0.3
0
1
2
3
4
5
6
7
8
9
10
11
Time [s ec]
12
13
14
15
16
17
18
19
Ipotesi Fondamentali:
- Nella pratica professionale non è necessario conoscere l’andamento nel tempo delle caratteristiche di
sollecitazione in ogni sezione dell’elemento strutturale, ma è sufficiente conoscerne il valore massimo.
- Nelle strutture tipiche dell’ingegneria civile (ad esempio edifici per civile abitazione) le masse strutturali sono
concentrate in massima parte in corrispondenza degli impalcati (solai).
- In alcuni casi (edifici in c.a.) gli impalcati possono essere considerati elementi indeformabili nel proprio piano,
e quindi in grado di connettere rigidamente tutti i nodi strutturali giacenti su di essi.
20
L’EFFETTO DEL SISMA SULLE STRUTTURE
L’effetto del sisma sulla struttura può essere considerato come l’applicazione al sistema di una
forza di tipo sinusoidale
 2  
F (t )  F  sin   t   F  sin 
t 
 T

L’applicazione di questa forza instaurerà sul sistema un regime di oscillazioni forzate il quale,
dopo una prima fase iniziale in cui saranno presenti anche le oscillazioni libere smorzate,
assumerà un forma analoga a quella delle oscillazioni libere ma con un periodo che adesso
sarà quello della forzante, con uno sfasamento rispetto ad essa ed un’ampiezza delle
oscillazioni che dipende dal rapporto F/k (F = valore massimo della forza, k = rigidezza del
sistema) e dal rapporto dei due periodi a = T0/T (T0 = periodo di vibrazione del sistema; T =
periodo di oscillazione della forza). Tale dipendenza è espressa dalla relazione seguente:
u (t ) 
1
(1  a 2 ) 2  4   2  a 2

F
F
 sin   t    A   sin   t  
K
K
L’EFFETTO DEL SISMA SULLE STRUTTURE
.
Caso 1
( = 0 ; a = 1)
Smorzamento nullo e periodo della forzante uguale al
periodo proprio della struttura, condizione detta di
“risonanza” (condizione teorica).
Caso 2
( piccolo ; a = 1)
Smorzamento piccolo e periodo della forzante
uguale al periodo proprio della struttura.
L’amplificazione è grande, ma ha valore finito.
Caso 3
(a = 0)
Periodo della forzante molto più grande del periodo
proprio della struttura. La massa segue la forza
come se si trattasse di tante condizioni statiche in
sequenza.
Caso 4
(a grande)
Periodo della forzante molto più piccolo del periodo
proprio della struttura. Il sistema oscillante, poiché la
variazione della forzante e molto rapida, non risente
dell’effetto, comportandosi come se questa non
fosse presente.
L’EFFETTO DEL SISMA SULLE STRUTTURE
ANALISI SISMICA DELLE STRUTTURE
Ipotesi Fondamentali:
- Nella pratica professionale non è necessario conoscere l’andamento nel tempo delle caratteristiche di sollecitazione in ogni
sezione dell’elemento strutturale, ma è sufficiente conoscerne il valore massimo.
- Nelle strutture tipiche dell’ingegneria civile (ad esempio edifici per civile abitazione) le masse
strutturali sono concentrate in massima parte in corrispondenza degli impalcati (solai).
- In alcuni casi (edifici in c.a.) gli impalcati possono essere considerati elementi indeformabili nel proprio piano, e quindi in grado
di connettere rigidamente tutti i nodi strutturali giacenti su di essi.
ANALISI SISMICA DELLE STRUTTURE
Analisi Sismica Classica
Analisi Sismica Nodale
ANALISI SISMICA DELLE STRUTTURE
Modello di calcolo
ANALISI SISMICA DELLE STRUTTURE
Modello di Calcolo
ANALISI SISMICA DELLE STRUTTURE
Analisi Sismica Classica
ANALISI SISMICA DELLE STRUTTURE
Analisi Sismica Classica
ANALISI SISMICA DELLE STRUTTURE
Analisi Sismica Nodale
ANALISI SISMICA DELLE STRUTTURE
Analisi Sismica Nodale
ANALISI SISMICA DELLE STRUTTURE
Analisi Sismica Nodale
ANALISI SISMICA DELLE STRUTTURE
Ipotesi Fondamentali:
- Nella pratica professionale non è necessario conoscere l’andamento nel tempo delle caratteristiche di sollecitazione in ogni
sezione dell’elemento strutturale, ma è sufficiente conoscerne il valore massimo.
- Nelle strutture tipiche dell’ingegneria civile (ad esempio edifici per civile abitazione) le masse strutturali sono concentrate in
massima parte in corrispondenza degli impalcati (solai).
- In alcuni casi (edifici in c.a.) gli impalcati possono essere considerati elementi indeformabili
nel proprio piano, e quindi in grado di connettere rigidamente tutti i nodi strutturali giacenti su
di essi.
MODELLI DI CALCOLO STRUTTURALE
IMPALCATI RIGIDI O DEFORMABILI
MODELLI DI CALCOLO STRUTTURALE
IMPALCATI RIGIDI O DEFORMABILI
Modello strutturale ad impalcato rigido
MODELLI DI CALCOLO STRUTTURALE
IMPALCATI RIGIDI O DEFORMABILI
Modello strutturale ad impalcato deformabile
IMPALCATI RIGIDI O DEFORMABILI
Schema telaio
IMPALCATI RIGIDI O DEFORMABILI
Deformata del telaio: Quota 3 = Piano Rigido
IMPALCATI RIGIDI O DEFORMABILI
Diagramma del Momento Flettente del telaio: Quota 3 = Piano Rigido
IMPALCATI RIGIDI O DEFORMABILI
Diagramma del Taglio del telaio:
Quota 3 = Piano Rigido
IMPALCATI RIGIDI O DEFORMABILI
Deformata del telaio: Quota 3 = Piano Deformabile
IMPALCATI RIGIDI O DEFORMABILI
Diagramma del Momento Flettente del telaio:
Quota 3 = Piano Deformabile
IMPALCATI RIGIDI O DEFORMABILI
Diagramma del Taglio del telaio:
Quota 3 = Piano Deformabile
IMPALCATI RIGIDI O DEFORMABILI
Deformata
Piano Rigido
Piano Deformabile
IMPALCATI RIGIDI O DEFORMABILI
Diagramma del Momento Flettente
Piano Rigido
Piano Deformabile
IMPALCATI RIGIDI O DEFORMABILI
Diagramma del Taglio
Piano Rigido
Piano Deformabile
ANALISI SISMICA DELLE STRUTTURE
- Analisi sismica Statica Lineare
- Analisi sismica Dinamica Lineare
- Analisi sismica Statica Non Lineare
- Analisi sismica Dinamica Non Lineare
ANALISI SISMICA DELLE STRUTTURE
Con il nome di analisi PUSH-OVER si indica una analisi
sismica statica incrementale NON LINEARE effettuata
per forze orizzontali monotonamente crescenti.
ANALISI SISMICA STATICA NON LINEARE PUSHOVER
• VERIFICA EDIFICI ESISTENTI
• Questo tipo di analisi è in pratica la via obbligata nel caso di verifiche di edifici
esistenti progettati solo per i carichi verticali, in questo caso una verifica elastica
risulta troppo penalizzante e di scarso interesse tecnico, solo un’analisi non
lineare è in grado di valutare in maniera realistica il grado di sicurezza della
struttura nei confronti del sisma
• VERIFICA NUOVI EDIFICI
La nuova normativa sismica prevede esplicitamente tale tipo di analisi per :
• valutare i rapporti di sovraresistenza
• valutare il reale fattore di struttura dell’edificio;
• come metodo di progetto per gli edifici di nuova costruzione sostitutivo dei metodi di
analisi lineari
ANALISI SISMICA STATICA NON LINEARE PUSHOVER
- D.M. 14 Gennaio 2008 7.3.6.2. VERIFICHE DEGLI ELEMENTI STRUTTURALI IN TERMINI DI DUTTILITA’ E
CAPACITA’ DI DEFORMAZIONE
Dovrà essere verificato che i singoli elementi strutturali e la struttura nel suo insieme possiedano
una duttilità coerente con il fattore di struttura q adottato. […]
[…] Alternativamente, e coerentemente con modello e metodo di analisi utilizzato, si deve
verificare che la struttura possieda una capacità di spostamento superiore alla domanda.
FATTORE DI STRUTTURA PER STRUTTURE IN C.A.
q  q0  K R
q0 = parametro funzione della tipologia strutturale e del livello di duttilità attesa
Tipologia Edificio
q0
au/a1
Strutture a telaio o miste equivalenti a telaio
Tipologia Strutturale
CD “B”
CD “A”
Strutture a telaio, a pareti accoppiate, miste
3.0 au/a1
4.5 au/a1
Strutture a telaio di un piano
1.1
Strutture a pareti non accoppiate
3.0
4.0 au/a1
Strutture a telaio multipiano ad una campata
1.2
Strutture a telaio multipiano a più campate
1.3
Strutture deformabili torsionalmente
2.0
3.0
Strutture a pendolo inverso
1.5
2.0
KR = parametro funzione della regolarità dell’edificio
KR
Tipologia Strutturale
1.0
Edifici Regolari in Altezza
0.8
Edifici Non Regolari in Altezza
Strutture a pareti o miste equivalenti a pareti
Strutture con solo due pareti non accoppiate per
direzione orizzontale
1.0
Altre strutture a pareti non accoppiate
1.1
Strutture a pareti accoppiate o miste equivalenti
a pareti
1.2
ANALISI NON LINEARE PUSH-OVER
L'esperienza fatta negli USA dal FEMA (la protezione civile americana) ha ormai consolidata l'utilizzo
nel campo dell'ingegneria civile della pushover analysis ovvero la più semplice delle analisi non
lineari possibili in quanto di tipo statica e con percorsi di carico di tipo monotonamente crescente.
- Domanda: moto sismico del terreno
- Capacità: abilità della struttura di resistere alla domanda sismica
- Prestazione: misura in cui la capacità assorbe la domanda
ANALISI SISMICA DELLE STRUTTURE
- Analisi sismica Statica Equivalente
- Analisi sismica Dinamica Modale
- Analisi sismica Dinamica Completa (Time History)
PERIODO DELLA STRUTTURA
T0  2   
m
k
Se si impone alla testa del piedritto uno spostamento orizzontale u0
(rispetto la posizione di riposo verticale) e successivamente lo si
lascia libero, sul sistema si instaurerà un regime di oscillazioni
libere caratterizzate da una andamento sinusoidale nel tempo con
un periodo di oscillazione T0, questo è il tempo che intercorre per
permettere al traverso di compiere un’oscillazione completa e
ritornare nella posizione iniziale. Tale periodo, detto anche periodo
proprio dell’oscillatore è legato alle due grandezze m e k (massa e
rigidezza) dalla seguente relazione:
L’EFFETTO DEL SISMA SULLE STRUTTURE
Oscillazione ideale
(smorzamento nullo)
Oscillazione reale
(smorzamento non nullo)
ANALISI SISMICA STATICA EQUIVALENTE
Le forze statiche equivalenti sono quelle che applicate alla struttura
producono gli stessi spostamenti indotti dal sisma
mu  cu  ku  mug  Peq
ANALISI SISMICA STATICA EQUIVALENTE
D.M. 1996
Fi  Wi  C    RT    I   i
Wi = massa del piano i-esimo dell’edificio
C = coefficiente di intensità sismica
 = coefficiente di struttura
R (T) = coefficiente di risposta
 = coefficiente di fondazione
I = coefficiente di protezione sismica
n
i = coefficiente di distribuzione
 i  hi 
W
j 1
n
W
j 1
j
j
 hj
ANALISI SISMICA STATICA EQUIVALENTE
D.M. 2008
Fi  Fh
Fh 
S d (T1 ) W  
g
zi Wi
 z j W j
zi , zj = altezze dei piani i-esimo e j-esimo dalla fondazione
Wi, Wj = pesi delle masse ai piani i-esimo e j-esimo
Sd(T1) = ordinata dello spettro di progetto in corrispondenza del valore T1 del periodo
T1  C1  H 3 / 4
H = altezza dell’edificio, espressa in metri, a partire dal piano di fondazione
Cl = coefficiente funzione della tipologia strutturale
W = peso complessivo della struttura
ANALISI SISMICA STATICA EQUIVALENTE
Le forze statiche equivalenti, secondo il D.M. 2008, si determinano graficamente a
partire dallo spettro di risposta.
f st ,i  Wtot   i  S e T1 
Se
f st ,i
zi
T1
T
TIPI DI ANALISI SISMICA
Analisi Sismica Statica - Distribuzione delle
forze sismiche equivalenti sulla struttura
.
CRITERI DI SCELTA DEL TIPO DI ANALISI
SISMICA
Requisito primario di applicabilità dell’analisi sismica statica è la regolarità
della struttura.
regolarità geometrica in pianta: intendendo con essa sia la regolarità geometrica
della pianta i cui elementi strutturali devono essere posti a distanze regolari, e sia la
regolarità della distribuzione delle rigidezze (ossia delle inerzie) degli stessi
elementi.
regolarità in elevazione: intesa come la proprietà da parte di tutti gli elementi
verticali che abbiano resistenza significativa all’azione sismica di estendersi senza
interruzione dalle fondazioni fino alla sommità dell’edificio, mantenendosi il rapporto
tra masse e rigidezze degli impalcati pressoché costante per tutta l’altezza.
distribuzione regolare dei pesi e dei carichi: assenza quindi di pannelli di
tamponamento, o di carichi sia permanenti che accidentali distribuiti sugli impalcati
in maniera asimmetrica.
CRITERI DI SCELTA DEL TIPO DI ANALISI
SISMICA
REQUISITO DI APPLICABILITA’ DELL’ANALISI
SISMICA STATICA (D.M. ‘96)
T1  0.1
H
 1.4 sec
B
H = massima altezza dell’edificio a partire dal piano di fondazione
B = massima dimensione in pianta dell’edificio
CRITERI DI SCELTA DEL TIPO DI ANALISI
SISMICA
REQUISITO DI APPLICABILITA’ DELL’ANALISI
SISMICA STATICA (Norme Tecniche 2005)
T1  C1  H 3 / 4  2.5  TC
H = massima altezza dell’edificio a partire dal piano di fondazione
Cl = coefficiente moltiplicativo funzione della tipologia strutturale, il
cui valore è riportato nel prospetto seguente:
C1 = 0.085
per edifici con struttura a telaio in acciaio
C1 = 0.075
per edifici con struttura a telaio in calcestruzzo
C1 = 0.050
per edifici con qualsiasi altro tipo di struttura
CRITERI DI SCELTA DEL TIPO DI ANALISI
SISMICA
REQUISITO DI APPLICABILITA’ DELL’ANALISI
SISMICA STATICA (Norme Tecniche 2005)
T1  C1  H 3 / 4  2.5  TC
TC  CC  TC*
Categoria del suolo
CC
A
1.0
B
1.10 (TC*)-0.20
C
1.05 (TC*)-0.33
D
1.25 (TC*)-0.50
E
1.15 (TC*)-0.40
CRITERI DI SCELTA DEL TIPO DI ANALISI SISMICA
Allegato A: Parametri spettrali di pericolosità sismica
ANALISI SISMICA STATICA EQUIVALENTE
 Si considerano solo i contributi dovuti alla prima forma modale. Non può essere
applicata a strutture non regolari in pianta o particolarmente deformabili.
 La distribuzione in altezza delle forze è determinata in forma approssimata. Non
può essere applicata a strutture non regolari in altezza.
 Il periodo fondamentale del sistema è solo un’approssimazione, a volte
grossolana, di quello reale.
 Si considerano i massimi valori delle forze. Non può essere applicata a strutture a
comportamento non lineare.
ANALISI SISMICA DINAMICA MODALE
1) Determinazione dei modi di vibrare della costruzione (analisi
modale).
2) Calcolo degli effetti dell’azione sismica, rappresentata dallo
spettro di risposta di progetto, per ciascuno dei modi di vibrare
individuati.
Modo n.1
3) Combinazione degli effetti relativi a ciascun modo di vibrare.
Modo n.3
Schema Strutturale
Modo n.7
ANALISI SISMICA DINAMICA MODALE
La risposta è data dalla sovrapposizione di più deformate semplici (forme modali) che oscillano con periodi differenti
m
m
i 1
i 1
u (t )   i  qi (t )   ui (t )
ANALISI SISMICA DINAMICA MODALE
m
m
i 1
i 1
u (t )   i  qi (t )   ui (t )
Nello spirito dell’analisi modale si ha:
interessano i valori massimi della risposta indotti dal sisma
u
(max)
i
 i  q
(max)
i

i

Se
 i  S e Ti ,  i 
2
i
Ti
T
che devono poi essere combinati fra loro:
u
( SRSS)
max

 u
m
i 1

(max) 2
i
Radice della somma dei quadrati (SRSS)
u
( CQC )
max

m
u
i 1
m
2
i , max
m
  ij  ui ,max  u j ,max
i 1 j 1
Combinazione Quadratica Completa (CQC)
TIPI DI ANALISI SISMICA
Analisi Sismica Dinamica
L’utilizzo dello spettro di risposta consente di calcolare gli effetti massimi del terremoto sulla costruzione associati a
ciascun modo di vibrare. Poiché durante il terremoto, tuttavia, gli effetti massimi associati ad un modo di vibrare non si
verificano generalmente nello stesso istante in cui sono massimi quelli associati ad un altro modo di vibrare, tali effetti non
possono essere combinati tra di loro mediante una semplice somma ma con specifiche regole di combinazione, di natura
probabilistica, che tengono conto di questo sfasamento temporale.
STot  S12  S22  ...  Sn2
n
n
n
S   S  
2
i 1
2
i
i 1
Si  S j
2
j 1 1   ij
Radice della somma dei quadrati (SRSS)
Combinazione Quadratica Completa (CQC)
TIPI DI ANALISI SISMICA
Analisi Sismica Dinamica
m partec.mod o  5%
m
i  eff
mtot
 0.85
TIPI DI ANALISI SISMICA
Analisi Sismica Dinamica - Distribuzione delle
forze sismiche equivalenti sulla struttura
.
ANALISI SISMICA DINAMICA MODALE
 richiede la determinazione di frequenze e forme modali del sistema, con
conseguente incremento dei tempi di calcolo
 i picchi massimi delle risposte associate ad ogni singola forma modale sono
combinati fra loro in forma approssimata, fornendo solo una stima della risposta
massima
 si considerano i massimi effetti indotti dal sisma alla struttura. Non può essere
applicata a strutture a comportamento non lineare
ANALISI SISMICA DINAMICA COMPLETA
(Time History)
E’ eseguire analisi dinamiche al passo applicando alla base della struttura, nelle tre direzioni principali, accelerogrammi a
tre componenti opportunamente selezionati.
Il risultato, per ogni analisi, è una time-history degli spostamenti nei nodi, indicando anche i massimi spostamenti relativi
di interpiano registrati durante l’analisi e lo stato di danneggiamento dei singoli elementi al termine del sisma.
ANALISI SISMICA DINAMICA COMPLETA
(Time History)
Consiste nel determinare le storie temporali delle risposte associate alle varie forme modali come soluzioni delle equazioni:
..
.
..
qi (t )  2   i  i  qi (t )    qi (t )  i  u g (t )
Si utilizzano accelerogrammi spettro-compatibili
2
i
CATEGORIA DEL SUOLO
Oscillatori differenti reagiscono in modo diverso ad uno stesso terremoto
1200
u
1139 cm s -2
T = 0.25 s
800
400
0
10
20
t
30
-400
-800
-1200
800
u
727 cm s-2
T = 0.50 s
400
400
PGA
0
10
20
-2
= 351 cm s
30
0
t
10
20
30
t
(s)
t
(s)
-400
(s)
-800
-400
Tolmezzo, Friuli, 1976
400
T = 1.00 s
u
0
-400
10
-252 cm s-2
20
30
(s)
SPETTRI DI RISPOSTA
Si può diagrammare il valore della
massima accelerazione ottenendo
lo spettro di risposta
dell’accelerogramma
Se
1200
cm s-2
800
1200
u
1139 cm s -2
400
T = 0.25 s
800
400
0
-400
-800
-1200
10
20
30
t
(s)
0
0
1
2
T
3s
SPETTRI DI RISPOSTA
Si può diagrammare il valore della
massima accelerazione ottenendo
lo spettro di risposta
dell’accelerogramma
Se
1200
-2
cm s
1139 cm s-2
800
1200
u
1139 cm s -2
400
T = 0.25 s
800
400
0
-400
10
20
30
t
(s)
0
0 0.25
-800
-1200
1
2
T
3s
SPETTRI DI RISPOSTA
Si può diagrammare il valore della
massima accelerazione ottenendo
lo spettro di risposta
dell’accelerogramma
Se
1200
-2
cm s
1139 cm s-2
800
800
u
400
727 cm s-2
T = 0.50 s
400
0
-400
10
20
30
t
(s)
0
0 0.25
-800
1
2
T
3s
SPETTRI DI RISPOSTA
Si può diagrammare il valore della
massima accelerazione ottenendo
lo spettro di risposta
dell’accelerogramma
Se
1200
-2
cm s
1139 cm s-2
800
800
u
400
727 cm s-2
T = 0.50 s
400
0
-400
727 cm s-2
10
20
30
t
(s)
0
0 0.25
-800
0.5
1
2
T
3s
SPETTRI DI RISPOSTA
Si può diagrammare il valore della
massima accelerazione ottenendo
lo spettro di risposta
dell’accelerogramma
Se
1200
-2
cm s
1139 cm s-2
800
727 cm s-2
400
400
T = 1.00 s
u
0
-400
10
-252 cm s-2
20
30
t
(s)
0
0 0.25
0.5
1
2
T
3s
SPETTRI DI RISPOSTA
Si può diagrammare il valore della
massima accelerazione ottenendo
lo spettro di risposta
dell’accelerogramma
Se
1200
-2
cm s
1139 cm s-2
800
727 cm s-2
400
252 cm s-2
400
T = 1.00 s
u
0
-400
10
-252 cm s-2
20
30
t
(s)
0
0 0.25
0.5
1
2
T
3s
SPETTRI DI RISPOSTA
Si può diagrammare il valore della
massima accelerazione ottenendo
lo spettro di risposta
dell’accelerogramma
Se
1200
-2
cm s
1139 cm s-2
800
727 cm s-2
400
252 cm s-2
0
0 0.25
0.5
1
2
T
3s
SPETTRI DI RISPOSTA
Si può diagrammare il valore della
massima accelerazione ottenendo
lo spettro di risposta
dell’accelerogramma
a/g
1
0.5
0
0
1
2
T
Si può quindi definire una curva che inviluppa tutti gli spettri di risposta, o che viene superata solo
occasionalmente
3s
CATEGORIA DEL SUOLO
.
ANALISI SISMICA DINAMICA COMPLETA
(Time History)
 richiede la generazione di accelerogrammi spettrocompatibili
 richiede l’integrazione di sistemi di equazioni differenziali (non lineari)
 l’interpretazione dei risultati risulta non immediata e può essere fatta solo su basi
statistiche
COMBINAZIONI SISMICHE
.
E ' x   E x  0.30  E y  0.30  E z
SISMA VERTICALE
- presenza di elementi pressoché orizzontali con luce superiore a 20 m
- presenza di elementi precompressi (eccetto solai con luce < 8m)
- presenza di elementi a mensola (con luce > 4m)
- presenza di strutture di tipo spingente
- presenza di pilastri in falso
- edifici con piani sospesi
- ponti
- edifici isolati (con rapporto tra la rigidezza verticale del sistema di isolamento Kv e la
rigidezza equivalente orizzontale Kesi inferiore a 800)
Nel caso di analisi non lineare statica (ad es, pushover analisys) non si applica la
combinazione delle due componenti orizzontali dell’azione sismica: l’analisi della
risposta strutturale è svolta considerando l’azione sismica applicata separatamente
secondo ciascuna delle due direzioni orizzontali.
COMBINAZIONI SISMICHE
D.M. ‘96
D.M. ‘08