Il terreno conduttore elettrico

Sicurezza Elettrica
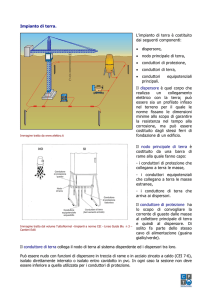
Il terreno
conduttore elettrico
1
La corrente elettrica quando attraversa il
corpo umano generalmente si richiude
tramite il terreno, tranne il caso in cui una
persona isolata da terra si trovi in contatto
simultaneo con due punti a diverso
potenziale.
La terra è anche coinvolta, direttamente o
indirettamente, in molti sistemi di protezione
terreno come conduttore elettrico
2
Resistenza di terra
Gli elettrodi immersi nel terreno
prendono il nome di dispersori.
Se consideriamo un dispersore
emisferico, sufficientemente
lontano dall’elettrodo di ritorno
possiamo scrivere per ogni strato
emisferico di terreno elementare di
raggio r e di spessore dr:
dr
dR   
2r 2
dr = “lunghezza percorsa” dalla corrente
2πr2 = “sezione attraversata” dalla corrente
ρ = resistività del terreno
3
Resistenza di terra
dr
dR   
2r 2
Ogni strato elementare offre una resistenza tanto più piccola
quanto più è lontana dal dispersore (maggiore sezione)

dr
 Resistenza di terra del dispersore emisferico
RT   

2
2r
2

r
2

r
0
r0
0
r0
la R del terreno equivale
a quella di un conduttore
elettrico di forma conica
R intorno al dispersore emisferico
di raggio r0
~
R conduttore di forma troncoconica
con base iniziale di raggio 2r0
e finale di raggio 2r
r
2r
dr
4
Resistenza di terra
I
A, B = dispersori di terra sufficientemente lontani
I = corrente che fluisce tra i due dispersori
è come se la corrente percorresse
il conduttore equivalente
A
B
I
B
A
• a distanza dai dispersori
la sezione del terreno è talmente grande che
la resistenza è quasi nulla
I
• in prossimità dei dispersori
A
B
le sezioni si restringono e aumenta la resistenza
del terreno
5
La R terreno è la somma delle R di terra dei due dispersori
Resistenza di terra
La resistenza del terreno compresa tra l’elettrodo emisferico di raggio r0
e l’emisfera di raggio 2r0 vale:
 dr
1
R 

RT
2
2 r
2r0
r
2 r0
0
metà della resistenza di terra di un
elettrodo emisferico è concentrata
nell’emisfero di terreno di raggio
doppio dell’elettrodo (terre artificiali)
• qualunque sia la forma del dispersore, a una distanza sufficientemente grande,
tutte le superfici equipotenziali divengono emisferiche
• equivalente emisferico di un dispersore di forma qualsiasi (RT): dispersore di forma

emisferica avente la stessa resistenza e raggio
r 
e
2RT
• il terreno è un conduttore elettrolitico
la resistività diminuisce con l’aumentare di
 umidità
 temperatura
• la resistività varia tra 1 e 10000 Ω con la natura geologica del terreno
6
I potenziali del terreno
La caduta di tensione dU
sullo strato emisferico elementare
di raggio r e spessore dr vale:
dr
 dU 
I
2
2r
Un punto del terreno posto a
distanza r assume un potenziale
(rispetto all’infinito)

dr
I
U  I

2
2r
2r
r
dove U∞=0
Andamento del potenziale
nel terreno percorso da corrente
7
I potenziali del terreno
I
Potenziale dell’elettrodo emisferico: U ee 
2r0
U ee

Resistenza di terra: RT 

I
2r0
Nel circuito (bipolo) equivalente alla RT i due poli sono rappresentati da:
1. Dispersore
2. Punto all’infinito a potenziale zero
Punto suff lontano dal dispersore
dove il potenziale sia trascurabile
(potenziale indisturbato)
8
Dispersori in parallelo
• 2 elettrodi emisferici di uguale raggio r0
• corrente dispersa I
• terreno omogeneo di resistività ρ
Ciascun elettrodo disperderà la corrente I/2
gli elettrodi assumono lo stesso potenziale
I 
I

U 
 
2 2 r0 2 2 (d  r0 )

2r0

2r0

4 (d  r0 )

1
RT 
4r0 1  r0
d
9
Dispersori in parallelo
Se d >> r0
i due dispersori possono considerarsi
in parallelo

2r0

2r0

RT 
4r0
Due elettrodi possono essere considerati in parallelo quando è zero il potenziale
prodotto dall’uno sull’altro.
In teoria i dispersori non sono mai in parallelo (solo all’infinito l’influenza reciproca è nulla)
In pratica è sufficiente che siano distanti circa d>10r0 per poter essere considerati in parallelo
(r0=raggio dell’equivalente emisferico del dispersore).
10
Resistenza verso terra di una persona
Piede = dispersore
2
RT 
5rp
piastra circolari di raggio rp
Uo
1
se rp 
m
10
RT  4
con ρ in Ωm
Piedi ~ 2 dispersori in parallelo
La resistenza della persona e del terreno fino un punto all’infinito vale: RC  RTC
resistenza corpo umano
Rc
Uc
Uo
Rtc
11
Tensione totale e tensione di contatto
carcassa di un apparecchio
TENSIONE TOTALE di terra
dispersore di resistenza RT
UT  RT I Guasto
TENSIONE di CONTATTO UC : tensione alla quale è soggetto il corpo umano durante un
guasto d’isolamento
U U
C
T
TENSIONE di CONTATTO a VUOTO UC0 : tensione preesistente al contatto tra la carcassa
e il punto del terreno occupato dalla persona
esempi …
12
Tensione totale e tensione di contatto
Es. 1)
Corrente di guasto I
struttura metallica della gru assume il potenziale UT
La persona si trova in un punto del terreno a
potenziale zero
soggetta a parte della UT
13
Tensione totale e tensione di contatto
Es. 2)
guasto d’isolamento
assume il potenziale UT rispetto all’infinito
La persona si trova in un punto in prossimità del
dispersore (punto a potenziale diverso da zero)
La resistenza della persona verso terra non è più in parallelo con RT
Il contatto della persona con la carcassa non
cambia apprezzabilmente UT ma modifica
l’andamento dei potenziali del terreno
solo una piccola parte della UT !
tra piedi e gru
14
Tensione totale e tensione di contatto
Es. 3)
la persona tocca contemporaneamente
il gancio della gru ed una
conduttura idrica
(buon collegamento con il terreno)
dispersore di bassa resistenza
RTA (<<RTC)
Uc maggiore
15
Contatti diretti ed indiretti
Se si entra in contatto con una parte dell’impianto
normalmente in tensione (conduttore, fusibile) che è
diventato casualmente accessibile si parla di contatto
diretto. Si dice contatto indiretto se una persona va in
contatto con una massa o
con una parte metallica
connessa ad essa durante
un guasto dell’isolamento. Il secondo è
sicuramente
il
più
pericoloso.
16
17