INTERVISTA AD UN GRANDE DELLA
MATEMATICA
BRIAN BUTERWORTH
FOCUS
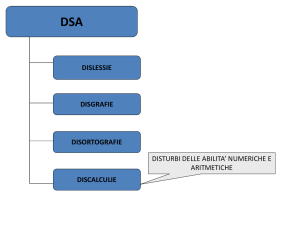
Mercoledì 29 settembre 2010 è stata approvata dal Senato la legge che riconosce e definisce
alcuni disturbi specifici di apprendimento (DSA) in ambito scolastico quali dislessia, disgrafia,
disortografia e discalculia.
Si riconosce l'esistenza di questi disturbi stimolando la scuola a individuarli precocemente e
definendo i luoghi del percorso diagnostico.
Viene sancito il diritto a usufruire dei provvedimenti compensativi e dispensativi lungo tutto il
percorso scolastico compresa l'Università e si assicura la preparazione degli insegnanti e dei
dirigenti scolastici.
PAROLA CHIAVE: DISCALCULIA O ACALCULIA
O ACALCOLIA
La discalculia è un Disturbo Specifico di Apprendimento (DSA)
che consiste nella difficoltà del calcolo e dell'elaborazione numerica.
Più precisamente si manifesta come:
– difficoltà nel leggere e scrivere numeri complessi (come quelli che
contengono lo zero) o lunghi (come quelli con molte cifre)
– difficoltà nell'esecuzione delle quattro operazioni scritte, dovuta al
mancato rispetto delle regole procedurali degli algoritmi
– difficoltà nel ripetere la maggior parte delle tabelline
– difficoltà in compiti relativi all'automatizzazione delle procedure di
conteggio, come ad esempio nel contare a salti, o contare all'indietro
LA RICERCA
La Discalculia è come una dislessia per i numeri
ma a differenza della dislessia poco si conosce al momento sugli
effetti, le cause e i trattamenti
Appare spesso in collaborazione con altre difficoltà di apprendimento
tra cui dislessia, disprassia, e disturbi da deficit di attenzione
ma la maggior parte degli studenti con discalculia possono avere abilità
cognitive e del linguaggio nel range di normalità e possono
effettivamente eccellere come soggetti non matematici.
Siamo a circa 20 anni indietro in termini di ricerca
e, più in particolare, in termini di riconoscimento da parte di genitori,
insegnanti, autorità scolastiche, e gli stessi studiosi della materia
rispetto alla dislessia.
L'entusiasmo con cui alcuni ricercatori e riabilitatori stanno discutendo.
L’INTERVISTA
Per approfondire il tema della discalculia interviene il professor
BRIAN BUTTERWORTH
Neuropsichiatra britannico
che da diversi anni si occupa di pazienti che hanno il problema
invalidante della gestione dei numeri.
Butterworth ha lavorato a lungo anche in Italia, a Padova e Trieste, e
ora insegna all'University College di Londra
Ha dedicato un libro al nostro rapporto con i numeri e alla loro radice
nella mente umana.
Brian Butterworth,
Intelligenza
matematica
1999, Rizzoli
Prima di entrare nello specifico della discalculia, vorremmo sapere
qualcosa sulla sua esperienza. Qual è stata la sua formazione
matematica, e come è arrivato a studiare le neuroscienze legate alla
matematica?
Ho fatto matematica fino a sedici anni a scuola, come tutti gli altri, senza essere
particolarmente bravo. Il vero interesse per la matematica l’ho avuto come studente
di filosofia, quando mi sono interessato ai fondamenti della matematica.
•
•
•
•
•
•
Mi sono spesso chiesto come le questioni fondamentali della matematica potessero
riguardare problemi psicologici
tanto da decidere di prendere una laurea in logica matematica.
Quello che realmente ha trasformato il mio interesse in un vero e proprio
programma di ricerca è stato avere a che fare con pazienti che presentavano delle
disabilità legate ai numeri.
Il loro linguaggio andava bene, la loro memoria era a posto, ma non potevano più
fare i calcoli che erano sempre stati in grado di fare.
Ho iniziato a pensare che forse avrei dovuto fare un po'di ricerca in questo settore,
perché nessuno a quel tempo sembrava approfondire il problema.
E nel 1984 ho incontrato lo psicologo americano Prentice Starkey, uno dei primi a
sostenere che i bambini hanno anche un senso del numero.
Chi è stato il tuo insegnante nel campo della discalculia?
L'unico mio vero insegnante credo sia stata
Elizabeth Warrington
•
•
•
Presso l'Ospedale Nazionale di Neurologia qui a Londra, che ha iniziato il primo
vero moderno studio neuropsicologico sulle abilità numeriche Certo, era in realtà
solo all’inizio della ricerca. Aveva un paziente che subì la perdita della capacità di
ricordare i numeri.
Fu la prima a scrivere che, forse, le abilità numeriche sono davvero un ramo
specializzato del nostro cervello e hanno una
specifica rappresentazione neurale
Nella "Prefazione" del suo libro, precisa di non essere un matematico e
di non essere particolarmente bravo neanche a far calcoli, però,
come chiunque altro, quotidianamente usa i numeri? Perché questo
è così evidente?
I numeri sono la base, anzi la materia prima del nostro pensiero.
•
Non potremmo rappresentarci il mondo se non in termini numerici.
•
Nuotiamo come pesci in un mare di numeri.
•
•
•
Ogni nostra azione, ma anche quasi ogni nostro pensiero, è contrassegnata da una
cifra o da una enumerazione: i numeri ci circondano, scandiscono la nostra presa
di possesso del mondo e il nostro operare in esso.
Misurano il tempo (minuti, ore, giorni, anni), le distanze (centimetri, metri,
chilometri), i nostri caratteri fisici, le nostre possibilità economiche e i nostri
guadagni, le finanze pubbliche e le rate del mutuo, le targhe delle auto e i codici
delle assicurazioni, l'altezza delle case, quella delle montagne e la profondità dei
mari, il peso dei bambini e la stazza delle navi e delle astronavi. E sono numero i
codici telefonici che ci consentono di comunicare tra noi come il prezzo del giornale
che state leggendo.
La scienza moderna ci consente di frequentare numeri enormi - quando misuriamo
in anni luce le profondità astronomiche - e infinitesimali, quando affondiamo nei
nanometri del microcosmo subatomico.
Da dove deriva questa familiarità che abbiamo con i numeri?
Grazie alla mia personale area di ricerca nella neuropsicologia dell'elaborazione
dei numeri, posso affermare che il genoma umano (l'insieme completo dei geni,
che fa di noi ciò che siamo) contiene le istruzioni per costruire circuiti cerebrali
specializzati chiamati, nel loro complesso,Modulo Numerico la cui funzione è quella
di "classificare il mondo in termini di quantità numerica, o numerosità...", mettendoci
nella condizione di percepire il numero di elementi di un insieme.Dunque non
abbiamo fatto altro che mettere in pratica ciò che è già potenzialmente in noi.
Cosa rappresenta il modulo numerico, e, fisicamente è possibile
localizzarlo come una zona specifica del nostro cervello?
Si tratta di una sorta di "kit di partenza" dal quale dipende tutto il successivo
sviluppo delle nostre capacità matematiche: in esso è inclusa la capacità innata di
riconoscere che un insieme di oggetti possiede una quantità esprimibile sotto forma
di numero quella che io chiamo una "numerosità" ordinata per grandezza: la
"numerosità" quattro include la "numerosità" tre, la due la uno, e così via. il Modulo
Numerico, rappresenta il nucleo centrale di tutte le nostre capacità matematiche e
intorno a questo nucleo costruiamo capacità matematiche più avanzate,
apprendendo dalla cultura da cui siamo circondati ciò che è già noto sui numeri.
•
•
•
Tale "Modulo Numerico", è innato sia nell'uomo che in specie non umane, non
funziona per numerosità oltre il 4 o il 5 al massimo e soltanto lo sviluppo e la
"trasmissione di strumenti culturali" ampliano le sue facoltà
L'area cerebrale che sembra essere fondamentale per i numeri é il lobo parietale
sinistro
Qui, probabilmente al confine fra il lobo occipitale, nella parte posteriore del
cervello che è il sito dei principali sistemi di elaborazione visivi, e il lobo temporale,
il sito della maggior parte dell'attività di elaborazione linguistica e della memoria
semantica', dovrebbe trovarsi il 'modulo numerico''.
In poche parole da cosa dipende la nostra capacità numerica?
Le capacità numeriche di ognuno dipendono da tre fattori:
•
il nucleo centrale innato, o modulo numerico le conoscenze matematiche della
cultura in cui siamo immersi la misura in cui ognuno ha acquisito tali conoscenze.
Insomma, tutti potenzialmente contano?
Non solo tutti contano ma voglio sottolineare che le capacità matematiche possono
essere migliorate grazie all'esercizio volontario.
•
•
•
•
•
In altre parole, utilizzando le sezioni del cervello che riguardano la capacità in
matematica ne provocano la dilatazione, e si può arrivare ad una migliore
elaborazione matematica.
Quindi non dovremmo essere sorpresi che a sinistra del lobo parietale di Einstein
Albert si sia riscontrata una concentrazione insolitamente alta di cellule cerebrali.
Einstein potrebbe essere nato con quelle cellule in piu' , oppure potrebbe averle
acquisite con l' esercizio. Forse le capacita' numeriche sono la causa, anziche' la
conseguenza, del maggior numero di neuroni.
In questo senso, il cervello non e' molto diverso dai muscoli: se fai certi movimenti
o certi sport, la muscolatura interessata si sviluppa di piu.
Oggi abbiamo le prove che i bambini possiedono questa facoltà fin dai primi mesi di
vita.
Come facciamo a sapere che i neonati sono in grado di effettuare
somme e sottrazioni?
Se mostrate ad un bambino una bambola, poi la coprite con uno schermo, e
mostrate una seconda bambola posizionandola dietro lo stesso schermo, il
bambino si aspetterà che ci siano due bambole quando lo schermo viene rimosso.
Se vi è un diverso numero di bambole -in più o in meno – il bambino se ne rende
conto e sarà sorpreso di vedere una somma con la risposta sbagliata!Questa
"violazione delle aspettative" è un esperimento che fu condotto da Karen Wynn nel
1992 presso l'Università dell’Arizona.Al momento della nostra nascita abbiamo
quasi tutti lo stesso potenziale per essere bravi in matematica.
Se tutti abbiamo le stesse potenzialità perché esiste la discalculia?
La discalculia nasce dal fatto che
•
•
tutti potenzialmente possediamo il modulo numerico
è ereditario, determinato da uno o più geni, in grado di classificare piccoli insiemi di
oggetti in base alla loro numerosità; qualcuno nasce con un cervello specializzato,
altri raggiungono la specializzazione solo con l'educazione, il training, ma c’è
chi..non ce l'ha.. ..perché è nato con una lesione oppure ha subito un danno
cerebrale, come un ictus o un
•
intervento chirurgico.
•
Si possono infatti distinguere:
•
• la discalcolia ad insorgenza tardiva, dovuta ad un ictus o come conseguenza di
un colpo in testa, appunto acalculia acquisita,
•
• dalla discalcolia dello sviluppo che è qualcosa che abbiamo dalla nascita.
•
Dal 3 al 6 per cento dei bambini nasce con danni cerebrali, e qualcuno,
praticamente uno per ogni classe di una trentina di alunni, viene al mondo con
un'incapacità congenita di far di conto, affetto cioè da discalcolia, spesso confusa
Come può un’insegnante riconoscere quando uno studente presenta
questo disturbo?
Gli studenti con discalculia possono dimostrare difficoltà nel comprendere anche
concetti semplici come il numero in sé di conseguenza presentano problemi di
apprendimento riguardo tutto ciò che riguarda i numeri e le loro procedure di
calcolo Anche quando gli studenti con discalculia sono in grado di produrre la
risposta corretta o il metodo corretto, lo possono fare in modo meccanico e senza
fiducia perché mancano di una comprensione intuitiva dei numeri, che tutti noi
possediamo. Per esempio possono imparare la sequenza di parole di un conteggio,
ma avere difficoltà nell’ordinare i numeri all’indietro. Essi possono anche trovare
particolarmente difficile tradurre in parole i numeri multipli di 10 espressi da nomi
nuovi, come "dieci", "cento", o "mille”.
Hai affermato che i metodi insegnamento influiscono sulle capacità di
fare calcoli. Cosa possono fare gli insegnanti per promuovere
l’apprendimento?
Sicuramente un primo passo può essere l’incoraggiare gli studenti ad applicare
diversi approcci per trovare la soluzione ad uno stesso problema questo li
aiuterebbe molto nel percorso dell’apprendimento matematico Nella matematica è
possibile arrivare alla stessa risposta attraverso strade diverse E 'importante che gli
insegnanti utilizzino il modo in cui insegnano per aumentare le capacità di cui gli
studenti sono in possesso. L’apprendimento della matematica è un processo
cumulativo, e se non si riesce a capire una fase, tutto ciò che è costruito su questa
fase resterà fragile.
Un esempio molto semplice: la didattica delle tabelline
I bambini cominciano a recitare la tabellina del due: «Uno per due, due; due per
due, quattro; tre per due, sei; quattro per due, otto» e così via. Quando riescono a
recitare questa tabellina alla perfezione, di solito passano a quella del tre, anche se
in certe scuole si salta direttamente a quella del cinque, dal momento che si pensa
che quest'ultima sia più facile da imparare di quella del tre o del quattro L'idea è
che a una certa età, di solito otto o nove anni, i bambini dovranno essere in grado
di recitare impeccabilmente le tabelline fino al dieci. Un bambino a cui avevo
chiesto di recitarmi le tabelline, snocciolò correttamente quella del due, ma rimase
perplesso quando chiesi: 6 x 2. Il fatto che fosse capace di recitare la sequenza
non significava che avesse capito che cosa significassero i componenti della
sequenza stessa.
Un'altra bambina a cui feci la stessa domanda riuscì a recitare sia quella del due
che quella del tre e rispose a un'altra mia domanda:
•
«Quanto fa 5 x 3?». Dopo un po' le chiesi: «Quanto fa 3 x 5?» Guardandomi con
aria di rimprovero mi redarguì: Non abbiamo ancora imparato la tabellina del
cinque.
•
Aveva indubbiamente imparato a rispondere alle prime due domande.
•
Ma è possibile, anche se non ne ho la prova diretta, che
•
•
•
•
la sua comprensione della proprietà commutativa della moltiplicazione fosse stata
ritardata dal fatto di essere stata costretta a imparare.
3 x 5 = 15 e 5 x 3 = 15 come dati del tutto separati.
Può darsi che l'apprendimento a memoria della tabellina del tre e dell'otto possa
condurre alla comprensione di 8 x 3 = 3 x 8. Potrebbe servire come una scala che
conduca alla comprensione e che poi possa essere gettata via.
Ma perché non cominciare assicurandosi che tutti i passaggi dell'apprendimento
abbiano un significato?
Ci sono prove che un metodo d’apprendimento differente porterebbe
ad una maggior capacità di calcolo?
Ci sono prove indirette:
•
•
•
•
•
•
Nei raffronti internazionali di competenze matematiche, di gran lunga i migliori sono
i cinesi, quelli della Repubblica popolare, di Taiwan e di Singapore.
Val la pena di osservare come il sistema scolastico cinese, relativamente positivo,
affronti la moltiplicazione.
Costringono forse i bambini a recitare le tabelline fino a nove per nove? No, non
fanno così.
Tanto per cominciare, i bambini non devono imparare la tabellina dell'uno. In
secondo luogo, non imparano 3 x 5 e 5 x 3.
Imparano 5 x 3 nella tabellina del tre, ma la tabellina del cinque comincia dal 5 x 5,
che ovviamente non rientra nelle tabelline precedenti del due, del tre e del quattro.
(...)
Questo metodo non solo riduce il carico mnemonico da 81 a 36 dati, ma aiuta il
bambino a capire che 3 x 5 e 5 x 3 sono equivalenti.
La scuola ha bisogno sempre di più dell’aiuto delle neuroscienze, per
apportare un miglioramento nei metodi utilizzati per l’insegnamento. Cosa
ne pensi è possibile questa unione tra scuola e neuroscienze?
L’istruzione e le neuroscienze sono al punto di partenza per una stretta
collaborazione. Più si parla dei problemi dell’apprendimento, più ci si rende conto
che siamo interessati a cercare soluzioni comuni forse la maggior parte degli
interessi all’inizio sarà focalizzato sui bisogni educativi specifici come
l'insegnamento della matematica a discalcolici o per i dislessici, e ad altri che
hanno ereditato disturbi che gli rendono difficile l’apprendimento, ma in futuro,
potremmo essere in grado di usufruire di teorie più generali su come il cervello
impara i concetti astratti e applicarle così alla scuola. Lì, penso che la grande
avventura tra scuola e neuroscienza si potrà dire veramente partita.
Un insegnante di matematica,indipendentemente da quanto ami la sua materia e
da quanto vigore metta nel suo desiderio di comunicarla,deve sempre affrontare
una difficoltà soverchiante: come tenere svegli gli studenti.
•
•
Mi è sempre sembrato che il modo migliore per rendere interessante la matematica
agli studenti e ai profani sia quello di accostarvisi con uno spirito giocoso.
Sta di fatto che il miglior modo di tener sveglio uno studente è presentargli giochi
matematici interessanti, enigmi, trucchi, battute, paradossi, modelli, o una qualsiasi
delle centinaia di cose che gli insegnanti ottusi tendono a evitare perché paiono
loro frivole.
•
(Brian Butterworth-riprende le parole di Martin Gardner)
Bibliografia utile – www
www.mathematicalbrain.com
www.dislessia.it
http://www.swif.uniba.it/lei/rassegna/butterwo.htm
archiviostorico.corriere.it
http://lanostramatematica.splinder.com
http://www.lalimonaia.pisa.it/news/numero.doc.htm
http://maristellina.wordpress.com
www.psicopedagogika.it