Teorema di Gauss

Il teorema di Gauss
Applicazioni
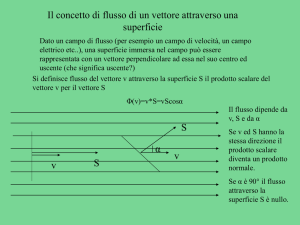
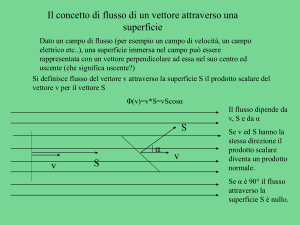
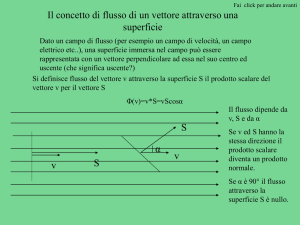
Il concetto di flusso di un vettore attraverso una
superficie
Dato un campo di flusso (per esempio un campo di velocità, un campo
elettrico etc..), una superficie immersa nel campo può essere
rappresentata con un vettore perpendicolare ad essa nel suo centro ed
uscente (che significa uscente?)
Si definisce flusso del vettore v attraverso la superficie S il prodotto scalare del
vettore v per il vettore S
Φ(v)=v*S=vScosα
Il flusso dipende da
v, S e da α
S
α
v
S
v
Se v ed S hanno la
stessa direzione il
prodotto scalare
diventa un prodotto
normale.
Se α è 90° il flusso
attraverso la
superficie S è nullo.
Flusso attraverso una superficie chiusa
Nel caso di un campo uniforme, il
numero delle linee di campo entranti
è lo stesso di quelle uscenti.
Il flusso totale è nullo
Nel caso in cui c’è una
sorgente che crea linee di
campo, il numero delle
linee di campo uscenti è
maggiore di quelle entranti.
Il flusso totale è
diverso da zero.
TEOREMA DI GAUSS
Il flusso del campo elettrico attraverso una
superficie chiusa è uguale alla somma delle
cariche racchiuse diviso la costante dielettrica.
Q

 (E) 
S
0
Il Teorema di Gauss è utile per il calcolo dei
campi elettrici di distribuzioni di cariche con
particolari simmetrie. Basta individuare il tipo di
simmetria e la corrispondente superficie
gaussiana attraverso cui calcolare il flusso del
campo.
Distribuzione di
carica
Simmetria
Proprietà dello
spazio
Superficie gaussiana
Campo elettrico
risultante
Carica puntiforme Q
Sferica
Isotropia
Superficie sferica con
centro in Q
E=KQ/r2
Densità di carica
superficiale σ su un
piano
Piana
Omogeneità
Superficie cilindrica
con asse
perpendicolare al
piano
E=σ/ε0
Densità di carica
lineare λ su una retta
Cilindrica
Isotropia
Superficie cilindrica
con asse il filo di
cariche
E=λ/2πε0r
Sfera di cariche con
densità di carica
volumica ρ
Sferica
Isotropia
Superficie sferica
concentrica con la
sfera di cariche
E=[Q/4πε0R3]r r<R
E=Q/4πε0r2 r>R
Superficie sferica di
cariche
Sferica
Isotropia
Superficie sferica
concentrica con la
sfera di cariche
E=0
E=Q/4πε0r2
Condensatore piano
carico
Piana
Omogeneità
Un cilindro con una
base parallela
esterna all’armatura
e una base interna.
E=σ/ε0
r<R
r>R
Carica puntiforme
E
E
La simmetria dello spazio è
sferica.
S2
S1
E
Scegliamo come superficie
gaussiana una sfera di centro la
carica Q
Dividiamo la superficie della
sfera in porzioni
rappresentati dai vettori
S1,S2…..Per simmetria il
campo elettrico E è costante
sull’intera superficie.
Q
E
Si ha:
 S ( E )  ES1  ES2  ....  ESn  E ( S1  S 2  ..  S n )  E 4r 2 
Q
0
E
1
Q
40 r 2
Piano di cariche
E
La simmetria dello spazio è piana.
S
E
Scegliamo come superficie gaussiana una
superficie cilindrica con asse perpendicolare al
piano
 S ( E )  2 ES 
S
Q
0

S

E
0
2 0
Il vettore E è perpendicolare al piano di cariche
di densità superficiale sigma e quindi il flusso di E
attraverso ogni piano di base del cilindro è E*S
S
mentre è nullo attraverso la superficie laterale
E
Linea retta di cariche
La simmetria è cilindrica
S
La superficie gaussiana è un cilindro con asse
la linea di carica.
E
Il campo E ha direzione perpendicolare alla
linea di cariche
S
E
Il flusso attraverso le basi è nullo.
Il flusso totale è quello attraverso la
superficie laterale.
 *l

 S ( E )  E * 2r * l 

E
0
0
20 r
Q
Sfera piena di cariche
La simmetria è sferica.
R

r
 S ( E )  E * 4r 2 
q
0
Q
E
Q
4 3
R
3
La superficie gaussiana è una superficie
sferica concentrica di raggio r. Il campo
elettrico all’interno della sfera è
proporzionale ad r. Per r=R si riottiene
l’espressione del campo elettrico di una
carica Q.
q
40 r 2
4 3
r
4 3 4 33
 r
R
Q
3
3
E


r
2
2
3
40 r
40 r
40 R
E
R
Se faccio un buco lungo tutto il diametro di una sfera carica positivamente,
quale sarà il moto di una carica negativa lasciata ad una uscita del buco?
r
Superficie sferica conduttrice carica
La simmetria è sferica.
La superficie gaussiana è una
sfera.
Se il raggio della superficie
gaussiana è r>R
R
Se il raggio della superficie
gaussiana è r<R
r
q  0   S ( E )  4r 2 E  0  E  0
r
E
 S ( E )  4r 2 E 
Q
0
E
1
Q
40 r 2
r
Condensatore piano carico
Il flusso del campo è nullo
attraverso la base nell’armatura
e attraverso la superficie
laterale.
Un condensatore è costituito da due
armature metalliche piane e
parallele.
La simmetria è piana
S
E
Prendiamo come superficie
gaussiana un cilindro con
una base parallela esterna
all’armatura e una base
interna.
Il flusso totale è dato da
quello del campo elettrico
attraverso la base posta tra
le armature.
S

 S (E)  E * S 

E
0 0
0
Q