Fisica Terrestre Parte I
Geodinamica e Paleomagnetismo
A. Caporali
Dipartimento di Geologia, Paleontologia e Geofisica
Università di Padova
Teoria della Terra Solida
Questioni di base:
• Come funziona la macchina terra, da un punto di vista meccanico, termodinamico
ed elettromagnetico
• Quali tecniche sperimentali usare per comprendere quantitativamente le leggi che
regolano questo funzionamento, validare modelli ed escluderne altri
Applicazioni della Teoria:
• Comprensione dei fenomeni ad elevato impatto sociale e ambientale quali
vulcanismo e terremoti
• Comprensione di alcuni meccanismi che possono portare alla formazione di bacini
sedimentari, e formazione di giacimenti
• Basi fisiche per comprendere gli strumenti e i metodi di prospezione geofisica
basati su effetti gravitazionali, elettromagnetici e elastico-meccanici
Struttura della Terra
Crosta e mantello: ricchi in silicati
Nucleo (interno e esterno): ricchi in
ferro
Spessore della crosta: 35 km in
media, c. 9 km negli oceani, fino a
70 km sotto gli orogeni
Moho: discontinuità di densità tra
crosta (2670 kg/m3) e mantello
(3300 kg/m3)
Profondità dell’interfaccia nucleo
(liquido)-mantello: c. 2900 km
Profondità dell’interfaccia nucleo
liquido – nucleo solido (non
mostrato in figura): 5100 km
Raggio terrestre medio: 6300 km
crosta
mantello
nucleo
Moho
Crosta/Mantello vs. Litosfera
Astenosfera
Distinzione Crosta/Mantello: ha basi sperimentali
gravimetriche e sismologiche ed è una distinzione di
densità di massa, legata all’equilibrio di forze verticali, o
isostasia
Distinzione Litosfera / Astenosfera : rappresenta invece
una variazione della reologia. La litosfera è rigida e
flessibile, la astenosfera tende a comportarsi come un
fluido viscoso. Chiaramente questo comportamento è
regolato dal gradiente geotermico. La geoterma critica che
marca la separazione litosfera – astenosfera corrisponde
a ~1400 K.
Lo spessore della litosfera è di circa 100 km e pertanto
contiene tutta la crosta e parte del mantello, il c.d.
mantello superiore.La astenosfera corrisponde al mantello
inferiore
Possiamo pensare alla litosfera come un guscio
meccanicamente rigido che galleggia sull’astenosfera che
è fluida per la elevata pressione e temperatura.
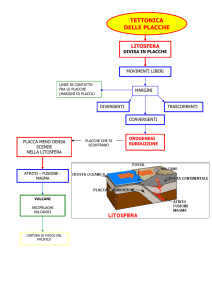
Introduzione alla Teoria della
Tettonica delle Placche (1/3)
La tettonica delle placche è la teoria che considera il guscio
esterno della Terra come suddiviso in placche, che si sono
mosse nel corso della storia della Terra. La teoria spiega come
e perchè si formano vulcani e catene montuose, si verificano
terremoti, e perchè nel passato animali simili tra loro possano
aver vissuto in zone e continenti che ora sono separati da
grandi distanze.
Circa 225 milioni di anni fa tutti i continenti maggiori erano
riuniti in un unico super continente chiamato Pangea
Forse a causa di un aumento del flusso di calore sotto questo
supercontinente, circa 220 milioni di anni fa la Pangea iniziò a
scomporsi. Gli oceani riempirono l’area compresa tra i
subcontinenti. I continenti continuarono a muoversi su placche
separate, finchè raggiunsero la posizione attualmente occupata.
Questo moto di deriva è tuttora in atto.
Esercizio: puzzle delle
placche (richiede
collegamento Internet)
Introduzione alla Teoria della
Tettonica delle Placche (2/3)
Il meccanismo che controlla il moto di deriva delle placche non è noto con esattezza. Una
teoria è che la convezione nel mantello della terra spinga le placche. In modo molto simile
, l’aria o l’acqua a contatto con una fonte di calore tende a migrare verso zone più fredde
(normalmente verso l’alto), per poi ridiscendere non appena raffredatasi.
Un’altra teoria è che la forza di gravità trascina verso il basso il fondo oceanico più vecchio,
e quindi più freddo e a maggiore densità (‘più pesante’). Nell’equilibrio verticale delle masse
il contrasto di densità svolge un ruolo fondamentale: masse più leggere tendono a
‘galleggiare’, masse più pesanti tendono a stare ‘in basso’. Per ‘leggero’ o ‘pesante’ si
intende ‘a minore densità’ o ‘maggiore densità’. Per comprendere come la differenza di
densità provochi galleggiamento si provi l’esercizio sull’isostasia (richiede collegamento
Internet) che illustra il galleggiamento di rocce di densità crostale (2700 kg/m3) immerse in
un fluido di densità simile a quella del mantello (3300 kg/m3)
Qualsiasi sia la forza che controlla la deriva delle placche, l’interazione tra le placche
avviene a quattro tipi di margini: margini divergenti, dove si forma nuova crosta; margini
convergenti, dove la crosta si consuma; margini collisionali, dove due placche continentali
collidono; e margini trascorrenti, dove due masse scivolano una rispetto all’altra.
Introduzione alla Teoria della
Tettonica delle Placche (3/3)
Lo spreading del fondo oceanico
(margine divergente)
Lo scivolamento
continentale (margine
convergente)
La collisione continentale
(margine collisionale)
Science Odyssey web site su Internet
Blocchi che si sfregano l’un
l’altro (margini trascorrenti)
Cinematica della rotazione
rigida
Teorema di Eulero: ogni movimento
traslazionale sulla sfera, per quanto
complicato, è sempre riconducibile a una
sequenza di rotazioni
Condizione di rigidità: la distanza relativa tra
due punti si mantiene costante nel tempo
Relazione fondamentale del moto rigido:
v r
Significato: la velocità del punto sulla placca è
sempre sul piano tangente alla sfera; non
esiste movimento verticale, perché il
prodotto scalare della velocità per il raggio
vettore è zero.
Punti appartenenti a una stessa placca con
velocità angolare costante hanno una
velocità lineare tanto maggiore quanto
maggiore è la loro distanza angolare
dall’asse di rotazione
v
Placca litosferica
in moto rigido
O
q
r
P
Traiettorie
sulla sfera
descritte da
punti della
placca
Calcolo della velocità (1/3)
Elementi identificativi del polo Euleriano:
le tre componenti del vettore velocità
angolare rispetto a un riferimento
geografico(x,y,z), con z diretto come
l’asse di rotazione terrestre, x sta sul
piano equatoriale e interseca il
meridiano di Greenwich, y completa la
terna destrorsa; oppure in coordinate
sferiche, assegnando il valore assoluto
di (modulo), la latitudine e longitudine
del punto intersezione dell’asse di
rotazione euleriano con la superficie
terrestre:
2
2
2
x cos( ) cos( ) x y z
y cos( ) sin ( ) sin 1 ( z )
z sin ( )
1
tan ( y / x )
z
x
y
Calcolo della velocità (2/3)
Componenti cartesiane
della posizione del
punto P, nota la sua
latitudine p, longitudine
p e distanza r dal
centro della terra:
Componenti cartesiane
della velocità lineare del
punto P: vengono
determinate
esplicitando il prodotto
vettoriale (NB: solo due
su tre sono
indipendenti, perché la
velocità è sempre
tangente alla sfera!)
x r cos( p ) cos( p )
y r cos( p ) sin ( p )
z rsin ( p )
vx y z z y
v y x z z x
vz x y y x
P
Calcolo della velocità (3/3)
Calcolo delle componenti Est e
Nord della velocità sul piano
tangente:
d
1. Vettori di base lungo il
vN r
meridiano e rispettivamente
dt
parallelo passanti per P
d
v E r cos( p )
dt
2. Differenziando le componenti
cartesiane del vettore OP
rispetto a latitudine e
longitudine di P (r=cost per
ipotesi!), si ottiene:
dx
sin ( p ) cos( p )v N sin ( p )v E
dt
dy
vy
sin ( p ) sin ( p )v N cos( p )v E
dt
dz
vz
cos( p )v N
dt
vx
vN
3. Risolvendo per vN,vE si ottiene:
vz r
x2 y2
v E v x sin ( p ) v y cos( p )
4. Modulo di v:
v r sinq
Ove q è l’angolo compreso
tra r e , e può essere
calcolato con i teoremi della
trigonometria sferica
(teorema del coseno)
Poli uscenti che interessano la
placca Eurasiatica
Eurasia-N.America
Eurasia-Pacifico
50
Arabia-Eurasia
India-Eurasia
Africa-Eurasia
0
-150
-100
-50
0
50
100
150
Placca
lat
lon
Omega (*10^-7
gradi/anno)
Africa-Eurasia
21
-20.6
1.3
Arabia-Eurasia
24.6
13.7
5.2
India-Eurasia
24.4
17.7
5.3
Eurasia-N.America
62.4
135.8
2.2
Eurasia-Pacifico
61.1
-85.8
9
Calcolo della velocità di un punto (Padova) della Placca Eurasiatica
rispetto alla placca N.America: Lat=45; lon=12 r=6371000m
componente
x
y
z
W (*10^-7
gradi/anno)
-0.73071
0.71059
1.94965
R (km)
4406.533
936.637
4504.977
V (cm/anno)
0.23999
2.07398
-0.66595
Padova
vN (cm/anno)
vE (cm/anno)
V (cm/anno)
Az(gradi)
-0.94
1.98
2.19
115
Velocità assolute delle placche
A.
B.
C.
Il modo in cui le velocità delle placche vengono
misurate dimostra che si tratta di velocità relative (di
una placca rispetto a quella contigua)
Per definire un moto assoluto, dobbiamo
Identificare una placca di riferimento
Calcolare il moto assoluto di questa placca
Il moto assoluto delle altre placche segue per
differenza
All’interno della placca del Pacifico vi sono delle strisce
quasi parallele di isole vulcaniche, con proprietà delle
rocce che fanno pensare a un flusso dal mantello. I
vulcani più a SE sono i più recenti
Si può pensare che come la placca pacifica transitava
sopra questi ‘hot spots’, sia rimasta una traccia. La
lunghezza delle strisce e la marca temporale dei
vulcani fornisce un valore assoluto della velocità della
placca del Pacifico
Quello degli hot spots non è però un sistema di
riferimento rigorosamente fisso: risulta infatti che
anche gli hot spots hanno cambiato posizione rispetto
al mantello
Velocità assoluta delle placche e
aree di massima compressione
Velocità assoluta
Massimo stress compressivo (vedi anche
la World Stress Map
Le zone dove si registra una brusca diminuzione di velocità sono quello dove si concentra lo sforzo
compressivo tra placche adiacenti
Esercizio: si verifichino quantitativamente i differenziali di velocità ai margini di placche adiacenti usando il
calcolatore di velocità assolute (richiede collegamento Internet)
Velocità attuale da dati GPS
Velocità assolute e relativa alla
placca Eurasiatica
v r v relativo
Paleomagnetismo
Perché interessa il campo magnetico terrestre (CMT)?
a)
Perché nel passato la direzione del CMT è stata variabile nel tempo, alternando, in modo non regolare,
inversioni di polarità
Perché alcune rocce, in particolare quelle basaltiche del fondo oceanico, hanno la capacità di ‘congelare’ al
loro interno la direzione del campo magnetico in un istante ben preciso della loro evoluzione termica
Perché il riconoscimento della sequenza dei successivi stati di magnetizzazione consente di dare una marca
di tempo ai campioni, e ricostruire la velocità di allontanamento relativo di due placche ai margini di un
‘ridge’ oceanico
Perché correlando velocità relative di placche adiacenti si può risalire alla posizione del polo euleriano e
ricostruire la cinematica a livello di placca
b)
c)
d)
a)
c)
b)
d)
Equazioni di Maxwell del Campo
Magnetico
O sia una superficie chiusa, e S un circuito chiuso delimitante una superficie
aperta
div B 0 B d A 0
O
D d A
D
rot H
j H ds
I
t
t
S
La prime equazione stabilisce l’inesistenza della carica magnetica; la seconda
equazione stabilisce che per generare un campo magnetico è necessaria o una
corrente elettrica o un campo elettrico variabile nel tempo
B= densità di flusso magnetico; H= campo magnetico
Relazione tra B e H: B=moH ove [H]=A/m, [B]=T=Vs/m2; mo=1.257 10-6
Vs/Am=4p*10-7 Tm/A
Campo Dipolare e non Dipolare
Un dipolo magnetico produce un campo
magnetico simile a quello di un ago
magnetizzato
Possiamo pensare il campo di dipolo
come il campo prodotto da correnti
elettriche che circolano lungo circuiti
ortogonali all’asse magnetico, con
intensità costante nel tempo, da Est
verso Ovest
Il CMT assomiglia al campo di un dipolo,
con l’asse dipolare attualmente orientato
che il polo Nord magnetico intercetta la
superficie terrestre a 79S e 109E
(Emisfero meridionale!!)
La porzione di CMT non descritta dal
campo dipolare si chiama campo non
dipolare.
Il campo dipolare che meglio riproduce in
media il CMT è derivabile da un
potenziale (m=7.94 1022 A m2):
m
V (r ) 0 3 m r
4pr
N
q
r
m
S
Il campo è :
B gradV
grad (
m 0 m cos
)
2
4pr
Componenti radiale e
tangenziale di B
Componente radiale di B: rappresenta la
variazione del potenziale lungo r: per
convenzione
V 2m 0 m cosq
Br Z
r
4pr 3
Componente tangenziale di B: rappresenta la
variazione di B lungo le linee di flusso, a r=cost:
Bq H
1 V m 0 msinq
r q
4pr 3
Inclinazione I di B rispetto al piano orizzontale
(= latitudine magnetica):
tan I
Z
2 cot q 2 tan
H
Declinazione d: è l’azimuth di H rispetto al Nord
(cf carte topografiche)
Notiamo che non esiste componente
longitudinale di B, causa la simmetria di V
Nord geomagnetico
H
I
B
q Z
Magnetizzazione nelle rocce
Le rocce vulcaniche, raffreddandosi, possono magnetizzarsi spontaneamente, allineando i dipoli al campo
magnetico terrestre di quel momento.
Al di sotto di una determinata temperatura, il campo magnetico delle rocce diventa permanente e rimane
come ‘congelato’ nella roccia
Per precisare quanto sopra, introduciamo il concetto di suscettibilità magnetica cm come la costante di
proporzionalità tra il campo magnetico esterno H e il momento magnetico M indotto nella roccia
M cm H
Per sostanze ferromagnetiche, la suscettibilità è regolata dalla legge di Curie e può essere molto elevata
nei dintorni di una temperatura q caratteristica della roccia, detta temperatura di Curie: (C= costante del
materiale)
cm
C
T q
Valori indicativi della temperatura di Curie sono intorno ai 600 C, molto inferiori alle temperature (800-1000
C) alle quali la lava cristallizza. Di conseguenza, quando la roccia oceanica arriva alla temperatura di Curie,
è già allo stato solido. Tale magnetizzazione è chiamata termorimanente.
Se B0=m0m/4pR3= 3 104 nT è il campo dipolare all’equatore, il campo indotto in basalti oceanici è circa 1%.
Concludiamo che l’ampiezza delle variazioni del CMT indotte nel magnetismo delle rocce è dell’ordine delle
centinaia di nT.
N
Posizione del Paleopolo
Su un campione ad es. di basalto
oceanico si misura:
1.
2.
3.
la posizione geografica attuale (x,x) del
campione di roccia
L’Inclinazione I del campo magnetico
della roccia
La declinazione d del campo magnetico
della roccia
L’inclinazione I permette di calcolare la
latitudine magnetica della roccia
all’epoca di magnetizzazione :
tan(I) = 2 tan()
La declinazione e l’inclinazione
permettono di calcolare la posizione
(P,P) del polo paleomagnetico
In figura: N= nord geografico,
X=posizione attuale del campione,
P=posizione del polo paleomagnetico
Nota: se p<x, sostituire d 360 - d
p-X
90-x
X
90-p
P
d
90-
Le formule di trigonometria sferica
necessarie per il calcolo sono:
sin ( P X )
sin d
sin (90 )
sin (90 P )
cos(90 P ) cos(90 X ) cos(90 )
sin (90 X ) sin (90 ) cos d
Misurabilità della
magnetizzazione
Per un dipolo Br ~ 2sin e Bq~cos,
ove è la latitudine del campione.
Di conseguenza, per un ridge che si
espande E-W, l’ampiezza
dell’anomalia sarà minima
all’equatore magnetico, dove solo la
componente tangenziale
contribuisce, essendo la
componente radiale nulla. A
latitudini maggiori o inferiori
(negative), l’ampiezza dell’anomalia
aumenta. Anomalie a latitudini
coniugate sono anticorrelate in fase.
Queste informazioni derivanti dal
modello sono molto utili per
migliorare la riconoscibilità delle
anomalie in presenza di rumore
Geomagnetic reversal time scale
E’ la scala che riassume lo stato
attuale delle nostre conoscenze
nella datazione della cinematica
del fondo ocoeanico
Si estende da 0 a 160 Ma
Nei primi 80 Ma contiene 33
fasce di inversione di polarità
magnetica
L’intervallo da 80 a 125 Ma
(Cretaceo) è caratterizzato da
una assenza di inversione
Da 125 a 157 Ma (Mesozoico)
l’attività di inversione è ripresa
Il fondo oceanico più vecchio
risale al Giurassico
Età del fondo oceanico
Proiezione Mercatore (chiaro = recente)
Oceano
Pacifico: Le
velocità sono
piccole
Oceano Atlantico: è il più semplice, a causa
dell’assenza di grandi zone di subduzione. Vi è
pura estensione. Coinvolge quattro placche: Nord
e Sud America, Africa e Eurasia. La separazione tra
Africa e S. America risulta iniziata circa 135 Ma,
mentre la separazione N.America Eurasia è
successiva (90 Ma)
Oceano Indiano: coesistono diversi ridges con offset
descritti dal lunghe faglie di scorrimento. La velocità non è
uniforme spazialmente: 1 cm/a sul versante W e 3 cm/a su
quello E. Esiste una importante zona di attiva subduzione,
il Java Trench. Il ridge compreso tra Australia e Antartide è
caratterizzato da una lenta espansione. Non sembra esserci
moto relativo tra India e Australia, ed è possibile che
appartengano alla stessa placca ‘Indo australiana’
Possibile ri-orientazione del Polo Euleriano nella
coppia Juan de Fuca - Pacifico
Proprietà dei Continenti
Continenti: inizialmente (280 Ma) erano
raggruppati in un supercontinente, il
Pangea, suddiviso in una parte
settentrionale (N.America, Eurasia)
chiamata Laurasia, e una parte
meridionale, Gondwana, comprendente S.
America, Africa, India, Antartide e
Australia. Nel Giurassico Laurasia e
Gondwana si sono separati e in mezzo si è
formato l’oceano Tethys. Il moto dell’India
e dell’Africa verso N NE ha portato alla
subduzione della Tethys sotto l’Eurasia. Il
Mediterraneo, il Mar Caspio e il Mar Nero
sono fossili della Tethys. La Catena alpinacarpatico Himalayana sono frutto della
collisione tra i due blocchi continentali.
Lungo queste catene vengono ritrovate
ofioliti, che sono sinonimo di rocce
oceaniche provenienti da antichi bacini di
retro arco.