0.1
0.1.1
Triangoli notevoli
Triangolo rettangolo con due angoli di 45◦
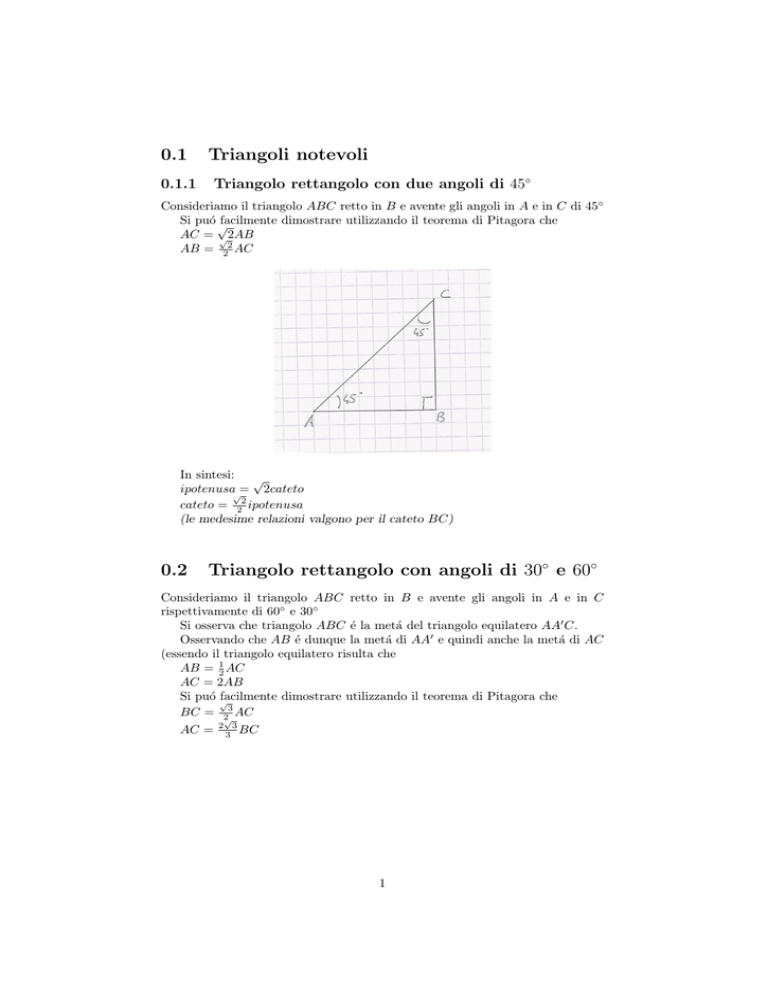
Consideriamo il triangolo ABC retto in B e avente gli angoli in A e in C di 45◦
Si puó √
facilmente dimostrare utilizzando il teorema di Pitagora che
AC = √ 2AB
AB = 22 AC
In sintesi: √
ipotenusa√= 2cateto
cateto = 22 ipotenusa
(le medesime relazioni valgono per il cateto BC)
0.2
Triangolo rettangolo con angoli di 30◦ e 60◦
Consideriamo il triangolo ABC retto in B e avente gli angoli in A e in C
rispettivamente di 60◦ e 30◦
Si osserva che triangolo ABC é la metá del triangolo equilatero AA0 C.
Osservando che AB é dunque la metá di AA0 e quindi anche la metá di AC
(essendo il triangolo equilatero risulta che
AB = 21 AC
AC = 2AB
Si puó √
facilmente dimostrare utilizzando il teorema di Pitagora che
BC = 23 AC
√
AC = 2 3 3 BC
1
In sintesi:
catetominore = 12 ipotenusa
√
catetomaggiore = 23 ipotenusa
0.3
0.3.1
Seno e coseno di angoli particolari
α = 30◦
Riferendoci all’ultima definizione data di seno e coseno consideriamo una circonferenza di raggio R = 1 e un angolo α = 30◦ . Indichiamo con P il punto
corrispondente all’angolo e con H e K le sue proiezioni sugli assi x e y. Il
triangolo rettangolo OP H ha un angolo di 30◦ e l’ipotenusa OP = 1
Utilizzando
le conoscenze sui triangoli notevoli deduciamo che:
√
OH = 23
OK = P H = 12
Quindi sen30◦ =
1
2
e cos30◦ =
√
3
2
2
0.3.2
α = 45◦
Considerando una circonferenza di raggio R = 1 e un angolo α = 45◦ . Indichiamo con P il punto corrispondente all’angolo e con H e K le sue proiezioni
sugli assi x e y. Il triangolo rettangolo OP H ha un angolo di 45◦ e l’ipotenusa
OP = 1
Utilizzando
le conoscenze sui triangoli notevoli deduciamo che:
√
OH = 22
√
OK = P H = 22
Quindi sen45◦ =
0.3.3
√
2
2
e cos30◦ =
√
2
2
α = 60◦
Considerando una circonferenza di raggio R = 1 e un angolo α = 60◦ . Indichiamo con P il punto corrispondente all’angolo e con H e K le sue proiezioni
sugli assi x e y. Il triangolo rettangolo OP H ha un angolo di 60◦ e l’ipotenusa
OP = 1
Utilizzando le conoscenze sui triangoli notevoli deduciamo che:
OH = 21
√
OK = P H = 23
3
Quindi sen60◦ =
0.3.4
√
3
2
e cos60◦ =
1
2
α = 120◦
Considerando una circonferenza di raggio R = 1 e un angolo α = 120◦ . Indichiamo con P il punto corrispondente all’angolo e con H e K le sue proiezioni sugli
assi x e y.
b = 30◦ e l’ipotenusa OP = 1
Il triangolo rettangolo OP K ha l’angolo P OK
b
Il triangolo rettangolo OP H ha l’angolo P OH = 60◦ e l’ipotenusa OP = 1
Utilizzando le conoscenze sui triangoli notevoli deduciamo che:
OH = 21
√
OK = P H = 23
√
3
2
Quindi, ricordando le considerazioni sul segno del seno e del coseno, sen120◦ =
e cos120◦ = 12
4
0.3.5
α = 135◦ ,α = 150◦ ,α = 210◦ ,α = 225◦ ecc...
Utilizzando una tecnica analoga é possibile calcolare il seno e il coseno di angoli
di 135◦ , 150◦ ,210◦ ,225◦ ,240◦ ,300◦ ,315◦ ,330◦ .
A questo punto si completi la seguente tabella riassuntiva:
α
0◦
30◦
45◦
60◦
90◦
120◦
135◦
150◦
180◦
210◦
225◦
240◦
270◦
300◦
315◦
330◦
360◦
sinα
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
5
cosα
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...












