Schede di Elettrotecnica
Corso di Elettrotecnica 1 - Cod. 9200 N
Diploma Universitario Teledidattico in
Ingegneria Informatica ed Automatica
Polo Tecnologico di Alessandria
A cura di Luca FERRARIS
Scheda N° 1
Circuiti in Corrente Continua:
• Serie e parallelo di resistenze
• Partitore di tensione
• Partitore di corrente
Scheda N° 1 - Circuiti in Corrente Continua:
Serie e parallelo di resistenze
RESISTENZE IN SERIE
2 o più bipoli si dicono connessi in serie se sono attraversati dalla stessa corrente.
n
R eq =
∑R
j
j =1
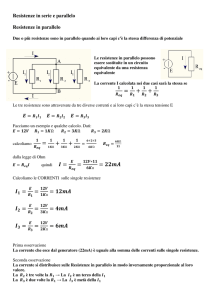
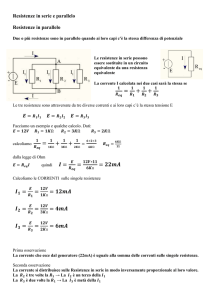
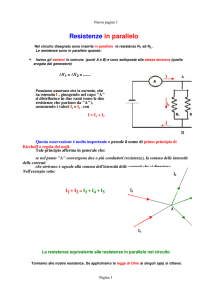
RESISTENZE IN PARALLELO
2 o più bipoli si dicono connessi in parallelo se sono sottoposti alla stessa tensione.
R eq
=
n
∑
j =1
1
R j
−1
PARTITORE DI TENSIONE
Formula generalizzata per un partitore di tensione costituito da n resistenze in
serie: la caduta di tensione sulla i-esima resistenza vale:
Vi = Vtot ⋅
Ri
n
∑R
j
j =1
FIGURA 1.13
PARTITORE DI CORRENTE
Formula generalizzata per un partitore di corrente
costituito da 2 resistenze in parallelo: la corrente nella
resistenza R1 vale:
A
R2
I1 = I tot ⋅
R1 + R 2
1
I1
I2
R1
R2
Itot
Scheda N° 1 - Circuiti in Corrente Continua:
Serie e parallelo di resistenze
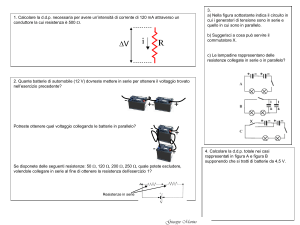
ESERCIZIO 1.1
Dato il circuito in fig. 1.1 calcolare la resistenza tra i capi A e B ponendo:
• R1 = 5 Ω
• R2 = 4 Ω
R1
R2
• R3 = 3 Ω
• R4 = 2 Ω
R3
R4
R AB = 7Ω
FIGURA 1.1
ESERCIZIO 1.2
Calcolare la resistenza equivalente tra i capi A e B del circuito in figura 1.4 con i seguenti dati
numerici:
•
•
•
•
R1 = 10 Ω
R2 = 40 Ω
R3 = 40 Ω
R4 = 20 Ω
RAB = 8 Ω
FIGURA 1.4
ESERCIZIO 1.3
Calcolare la resistenza equivalente tra i capi A e B del circuito in figura 1.7 con i seguenti dati
numerici
• R1 = 10 Ω
• R2 = 20 Ω
• R3 = 60 Ω
FIGURA 1.7
R AB
1
1
1
=
+
+
R1 R 2 R 3
FIGURA 1.8
−1
1
1
1
= +
+
10 20 60
2
−1
6 + 3 + 1
=
60
−1
=
60
=6Ω
10
Scheda N° 1 - Circuiti in Corrente Continua:
Serie e parallelo di resistenze
ESERCIZIO 1.4
Calcolare la resistenza equivalente tra i capi A e B del circuito infinito in figura 1.9.
FIGURA 1.9
R EQ = R •
1+ 5
= 1,618R
2
ESERCIZIO 1.5
Calcolare la resistenza equivalente tra i capi A e B del circuito in figura 1.11 ponendo tutte le
resistenze con un valore di 1000 Ω.
RAB = 631,58 Ω
FIGURA 1.11
3
Scheda N° 1 - Circuiti in Corrente Continua:
Serie e parallelo di resistenze
ESERCIZIO 1.6
Con riferimento alla figura 1.13 calcolare le tensioni (V1 e V2) che sussistono ai capi delle resistenze
R1 e R2 con questi dati:
• VAB =100 V
• R1 = 0,5 Ω
• R2 = 1 Ω
Applicando la formula del partitore di tensione si ottiene
FIGURA 1.13
R1
= 33,33 V
R1 + R 2
R2
V2 = VAB ⋅
= 66,66 V
R1 + R 2
V1 = VAB ⋅
ESERCIZIO 1.8
Dato il circuito in figura 1.14, calcolare la tensione tra capi B e C ponendo questi dati:
•
•
•
•
VAB = 300 V
R1 = 20 Ω
R2 = 50 Ω
R3 = 1) 100 Ω
2) 3000Ω
3) 1Ω
• R3 = 100 Ω
• R3 = 3000Ω
• R3 = 1Ω
⇒
⇒
⇒
V2 = 187,5 V
V2 = 213,27 V
V2 = 14 V
FIGURA 1.14
4
Scheda N° 1 - Circuiti in Corrente Continua:
Serie e parallelo di resistenze
ESERCIZIO 1.9
Calcolare la resistenza equivalente tra i capi A e B del circuito rappresentato in figura 1.15 in cui
tutte le resistenze hanno valore uguale e pari a R.
R2
R3
R4
R1
B
A
R5
R10
R8
R6
R9
R7
FIGURA 1.15.
−1
R eq
1
1
15
=
+
R = 0,79 R
=
19
R 18 R 17
5