Revisione del 1/10/15
ISTITUTO TECNICO INDUSTRIALE “V.E.MARZOTTO” – Valdagno (VI)
Corso di Fisica – prof. Nardon
FUNZIONI – DIPENDENZA LINEARE
Richiami di teoria
Rappresentazione matematica di una dipendenza lineare
Y = aX + b
Con a, b valori costanti. Notare che, se b = 0, la funzione diventa Y = aX, cioè una proporzionalità diretta.
N.B. Non è importante l’ordine con cui i termini sono presenti nella formula.
Es.
Y = 3X + 4 equivale perfettamente a Y = 4 + 3X
Rappresentazione grafica
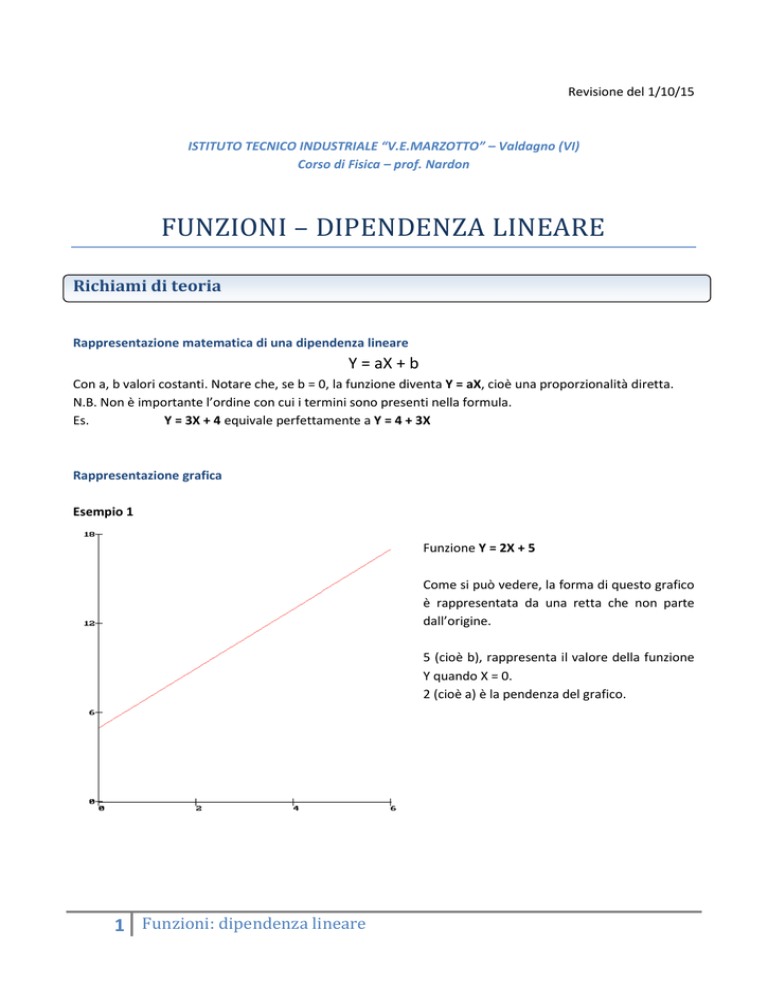
Esempio 1
Funzione Y = 2X + 5
Come si può vedere, la forma di questo grafico
è rappresentata da una retta che non parte
dall’origine.
5 (cioè b), rappresenta il valore della funzione
Y quando X = 0.
2 (cioè a) è la pendenza del grafico.
1 Funzioni: dipendenza lineare
Esempio 2
Funzione Y = -3X + 6
Anche questa è una retta, ma questa volta è
inclinata verso il basso, perché la pendenza (-3) è
negativa.
Esercizi svolti
Esercizio 1:
Scrivere la funzione per la seguente tabella:
X
0
2
Y
5
0
Dalla tabella
alla funzione
Poiché si tratta di una dipendenza lineare, la funzione ha la forma base Y = aX + b; utilizziamo le
due coppie X,Y per sostituire X e Y nella funzione di base e trovare a e b:
1.
2.
5 = a*0 + b = b (perché a*0 = 0)
0 = a*2 + b
Dalla prima equazione ricaviamo quindi:
b=5
Ora sostituisco il valore di b nella seconda equazione
0 = a*2 + 5
Porto il +5 al primo membro (cambiandolo di segno):
-5 = a*2
Divido ambo i membri per 2:
=
=a
Quindi:
a=
La formula finale, ora che abbiamo a e b, è:
Y=
2 Funzioni: dipendenza lineare
X+5
Esercizi
[N.B. la difficoltà degli esercizi va da (semplice) a (impegnativo)]
Esercizio 1
Rappresentare in grafico cartesiano le seguenti dipendenze lineari:
1.1.
Y = 5X + 3
1.2.
Y = X -2
1.3.
Y = -4X + 1
1.4.
Y=
+2
1.5.
Y= –3
1.6.
1.7.
Y = -7 – X
Y=4
1.8.
Y = 3/5 +
1.9.
1.10.
Y = (X+3)/6
Y = -3X + 1/3
Esercizio 2
Convertire le seguenti tabelle di dipendenza lineare in funzioni:
2.1.
2.2.
2.3.
2.4.
X
0
2
X
0
-3/2
Y
2
-1/3
2.6.
X
0
3/2
X
0
-3
Y
-3
0
2.7
Y
-3
0
X
0
1/7
X
0
2
Y
4
5
2.8.
Y
-2
-1
X
0
3
3 Funzioni: dipendenza lineare
2.5.
Y
3/2
0
2.9.
Y
1/3
13/3
X
0
-1
X
0
5
Y
1/5
-4/5
2.10.
Y
1
0
X
0
2
Y
1
0
Soluzioni degli esercizi
1.1.
1.2.
4 Funzioni: dipendenza lineare
1.3.
1.4.
5 Funzioni: dipendenza lineare
1.5.
1.6.
6 Funzioni: dipendenza lineare
1.7.
1.8
7 Funzioni: dipendenza lineare
1.9.
1.10.
2.1. Y = 6X+2
2.6. Y = 2X-3
2.2. Y = -X-3
2.7 Y = 7X-2
2.3. Y = X/2+4
2.8. Y = 4X/3+1/3
8 Funzioni: dipendenza lineare
2.4. Y = X+3/2
2.9. Y = X+1
2.5. Y = -X/5+1/5
2.10. Y = -X/2+1