In questa lezione impareremo...
◗◗ a conoscere l’istruzione di ciclo precondizionato o a condizione di testa
◗◗ a utilizzare la trace table per verificare ◗
i programmi
◗◗ il teorema di Jacopini-Böhm
LEZIONE 7
Il ciclo
a condizione
iniziale
■■ Il ciclo a condizione iniziale: while ... { ... }
Nella vita quotidiana ci sono delle operazioni che devono essere ripetute più volte, fino a
quando non si raggiunge un determinato obiettivo.
Esempi di questo tipo di operazioni possono essere i seguenti:
◗◗ versa l’acqua nel bicchiere finché è pieno;
◗◗ aggiungi sale al risotto quanto basta;
◗◗ lava la moto finché è pulita;
◗◗ disponi i libri sulla libreria finché sono ordinati;
◗◗ mentre non piove, taglia l’erba del giardino;
◗◗ somma i numeri che leggi finché la somma è minore di 100;
◗◗ … e via di seguito.
In queste situazioni non è peraltro possibile stabilire quante volte un’azione deve essere eseguita,
ma sappiamo solamente quando deve terminare.
Siamo dunque in presenza di situazioni nelle
quali si deve ripetere ciclicamente, o iterare, le
istruzioni sotto il controllo di un test, chiamato
condizione di ingresso al ciclo.
La figura strutturale che descrive queste situazioni è riportata a lato. ▶
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
1
UdA 7
Il linguaggio C
In linguaggio di programmazione viene così tradotta:
while <condizione di ingresso>
{<blocco di istruzioni>};
Distinguiamo ogni singolo elemento che la compone:
parola
chiave
condizione
inizio
blocco
corpo
del ciclo
fine
blocco
fine
istruzione
while
<condizione>
{
<istruzioni>
}
;
Si ricorda che la <condizione> deve sempre essere messa tra parentesi tonde (), bisogna
cioè scrivere (<condizione>).
Il funzionamento è semplice:
◗◗ viene valutata la condizione di ingresso, che è un’operazione di test, e quindi ha risultato
VERO o FALSO;
◗◗ quando il risultato è VERO si entra nel ciclo e si esegue il blocco di istruzioni (o semplicemente un’istruzione);
◗◗ al termine dell’esecuzione del blocco si torna indietro, a ripetere il test, cioè si ripete
l’esecuzione della condizione logica di ingresso:
––se l’esito è ancora VERO si ripete il ciclo;
––se è FALSO, si esce dall’altro ramo e si prosegue il programma con le successive istruzioni.
L’istruzione può essere letta nel seguente modo: “mentre la condizione è verificata (cioè
il test dà esito VERO) fai il blocco di istruzioni”.
Vediamo un primo esempio.
ESEMPIO
Divisione di un numero per 2
Letto un numero intero, dividiamolo per 2 mentre è maggiore di 2.
2
◀ Per come è strut­
turato il ciclo a condizione iniziale, il
blocco di istruzioni
(corpo del ciclo) po­
trebbe anche non
essere mai eseguito
neppure una volta:
basta infatti che la
condizione di in­
gresso dia subito ri­
sultato FALSO. ▶
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
Il ciclo a condizione iniziale
Lezione 7
Per verificare il corretto funzionamento di un ciclo si utilizza la tabella di traccia (o trace
table): in questo caso abbiamo solamente una variabile e seguiamo come viene modificato
il suo valore inserendo per esempio 60 come numero letto.
Numero istruzione
Istruzione di test
6
60
VERO
7
9
60 / 2 = 30
VERO
7
9
30 / 2 = 15
VERO
7
9
15 / 2 = 7
VERO
7
9
7/2=3
VERO
7
9
3/2=1
FALSO
7
11
◀ Il ciclo a condizione
iniziale è anche detto
ciclo precondizionato o
a condizione di testa. ▶
numero
(si esce dal ciclo)
1
Si osservi che sono sempre presenti coppie di istruzioni 7 e 9 (test
e divisione), in quanto l’istruzione di test permette l’ingresso al
ciclo e solo se questa ha valore VERO viene eseguito il ciclo; il test
quindi viene sempre eseguito prima del contenuto del ciclo: per
questo prende anche il nome di ◀ ciclo a condizione iniziale ▶.
In questo esempio il corpo del ciclo, cioè le istruzioni che devono essere ripetute nel ciclo, si
riduce alla sola operazione di divisione: è possibile, in questo caso, scrivere questa istruzione,
racchiusa tra parentesi graffe, su una sola riga:
Dato che il corpo del ciclo è una sola istruzione, potrebbe anche essere scritta senza { }:
8 numero=numero/2;
Prova adesso!
• Utilizzare il ciclo while
• Visualizzare la trace table
APRI IL FILE diviso2.c
Aggiungi all’interno del ciclo un’istruzione che visualizza il valore della variabile numero,
visualizza cioè la trace table.
Confronta il risultato con quello del file diviso2Sol.c.
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
3
UdA 7
Il linguaggio C
ESEMPIO
Somma dei numeri
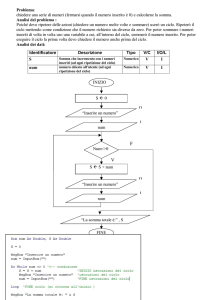
Scriviamo un programma che legge un numero e calcola la somma di tutti numeri compresi
tra 1 e il numero letto: per esempio, se viene inserito 4 esegue il calcolo della somma dei
primi 4 numeri, cioè: 1 + 2 + 3 + 4 = 10.
La soluzione di questo esempio è più complessa, in quanto richiede di compiere più operazioni: dobbiamo eseguire una somma di un numero di addendi che al momento della
scrittura del programma non è noto, ma tale numero verrà inserito dall’utente.
Dobbiamo quindi realizzare un meccanismo che continui a eseguire la somma di due numeri
alla volta per tante volte quanto indicato dal numero inserito: memorizziamo ogni somma
parziale in una variabile chiamata totale e in essa, alla fine, sarà presente il risultato.
Il codice in C è il seguente:
Il contatore viene detto variabile di controllo del ciclo.
Seguiamo la trace table inserendo 4 come numero in input.
Numero del ciclo
Numero Istruzione
contatore<numero
numero
5-6
8
9
1
11
1
12
9
2
11
2
12
9
3
11
3
12
9
4
11
4
12
9
14
4
contatore
totale
0
0
4
VERO
1
1
VERO
2
3
VERO
3
6
VERO
4
10
FALSO
(si esce dal ciclo)
10
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
Il ciclo a condizione iniziale
Lezione 7
Le istruzioni del ciclo sono state eseguite 4 volte, quindi il ciclo è stato ripetuto come desideravamo, in modo da effettuare le 4 somme desiderate.
Al totale è stato sommato proprio il valore del contatore in quanto assume i valori degli
addendi che dobbiamo sommare, cioè 1 + 2 + 3 + 4.
• Utilizzare il ciclo while
• Usare un contatore a decremento
• Operatore di decremento --
Prova adesso!
APRI IL FILE sommaNaturali.c
Modifica il ciclo cambiando la condizione di ingresso in questo modo:
while(contatore>0)
utilizza cioè un contatore a decremento.
Confronta il risultato con quello riportato nel file sommaNaturaliSol.c e con quello riportato
nel file sommaNaturaliSol2.c, dove non è stata usata una variabile di conteggio, ma viene
direttamente utilizzato il numero inserito anche come contatore.
GAUSS E LA SOMMA DEI PRIMI 100 NUMERI NATURALI
Si dice che Gauss avesse determinato in poco tempo, durante le elementari, la somma
dei primi 100 numeri naturali, rispondendo alla richiesta del maestro che lo voleva tenere impegnato per un po’ di tempo per potersi dedicare anche agli altri bambini.
Il piccolo Gauss osservò che la somma dei termini della successione equidistanti dal termine mediano è costante, come si può constatare dalla seguente organizzazione dei dati:
1
2
3
4
5
6
7
8
9
10
11
Questo disegno suggerì a Gauss la formula per ottenere direttamente la somma di n numeri:
n(n + 1)
S(n) = –––––––
2
che ancora oggi porta il suo nome.
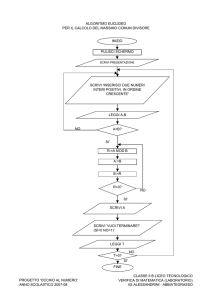
■■ Esempio: l’algoritmo di Euclide per il calcolo del MCD
Il Massimo Comun Divisore tra due numeri è il divisore comune a entrambi i numeri che
ha valore maggiore; per determinarlo è necessario quindi:
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
5
UdA 7
Il linguaggio C
◗◗ calcolare per ogni numero l’elenco dei divisori (dove per divisore intendiamo un numero
che divide perfettamente il numero dato senza produrre resto);
◗◗ individuare nei due gruppi di divisori il numero maggiore che hanno in comune.
EUCLIDE
Euclide, matematico greco nato ad Alessandria d’Egitto intorno al 300 a.C., è famoso per la
sua opera Elementi (in greco Stoichéia), dove tratta il procedimento per il calcolo del MCD in modo
geometrico. Al suo nome si legano il termine geometria euclidea o elementare (comprendente la geometria piana e la geometria solida), il postulato di Euclide e i due importanti teoremi di Euclide.
L’algoritmo di Euclide è il metodo con cui ◀ Euclide ▶ risolse, nel Libro 7 degli Elementi, il problema di come trovare il MCD tra due numeri interi positivi senza calcolare
tutti i divisori. L’idea alla base del procedimento è semplice: anziché calcolare il MCD di a e b, si divide a per b, si
trova il resto r e si calcola il MCD di b e r, che sono numeri più piccoli; si procede nello
stesso modo fino a quando si effettua una divisione che non produce resto.
Tale divisore è il MCD ricercato.
◀ Il metodo di Euclide è con­
siderato in molte enciclopedie
e vocabolari come un tipico
esempio di algoritmo. ▶
Vediamo per esempio come determinare il MCD di
Calcoliamo il primo resto dividendo:
Scambiamo tra loro i due numeri e otteniamo:
Scambiamo tra loro i due numeri e otteniamo:
Scambiamo tra loro i due numeri e otteniamo:
Il MCD è l’ultimo resto diverso da zero, cioè 5.
Schematicamente si procede in questo modo:
90 e 25.
90 e 25 → resto 15
25 e 15 → resto 10
15 e 10 → resto 5
10 e 5 → 0
numero1 % numero2 → resto
90
25
15
25
15
10
15
10
5
10
50
Vediamo altri esempi, calcolando il MCD di:
◗◗ 220 e 48: resto (220, 48) = 28, r (48, 28) = 20, r (28, 20) = 8, r (20, 8) = 4, r (8, 4) = 0 MCD = 4
◗◗ 624 e 246: resto (624, 246) = 132, r (246, 132) =114, r (132, 114) = 18, r (114, 18) = 6,
r (18, 6) = 0 MCD = 6
◗◗ 1540 e 1295: resto (1540, 1295) = 245, r (1295, 245) = 70, r (245, 70) = 35, r (70, 35) = 0
MCD = 35
La codifica in linguaggio C è immediata: vediamola nell’esempio che segue.
ESEMPIO
Algoritmo di Euclide
Eseguiamo ora la trace table con i numeri 936 e 324.
6
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
Il ciclo a condizione iniziale
Numero del ciclo
Numero istruzione
1
1
1
2
2
2
3
3
3
5
6
7
8
9
6
7
8
9
6
7
8
9
6
13
numero2>0
numero1
numero1
resto
936
324
0
Lezione 7
vero
288
324
288
vero
36
288
36
vero
0
36
falso
0
(si esce dal ciclo)
stampa(36)
Ma che cosa succede se numero2 è maggiore di numero1, oppure se vengono inseriti numeri negativi? Per verificarlo, svolgi l’esercizio proposto di seguito.
Prova adesso!
• Utilizzare il ciclo while
• Usare l’algoritmo di Euclide
APRI IL FILE euclide.c
Modifica il programma controllando la correttezza di numero1>numero2, eventualmente
scambiando i numeri tra di loro nel caso non fosse verificata.
Confronta la tua soluzione con quella riportata nel file euclideSol.c.
Modifica il programma controllando l’inserimento di numeri positivi.
Confronta la tua soluzione con quella riportata nel file euclideSol2.c.
■■ Teorema di Jacopini-Böhm
Con l’istruzione di iterazione si apre un “nuovo orizzonte” per la scrittura degli algoritmi;
essa, come la concatenazione e la selezione, è una figura fondamentale della programmazione strutturata. Oltre a quelle citate esistono altre figure strutturali, come l’istruzione di
salto; questa è stata esclusa dalla programmazione strutturata essendo la principale causa
del cosiddetto “codice-spaghetti”, quel codice cioè scritto in modo tanto ingarbugliato da
non poter essere compreso neanche dallo stesso programmatore.
La teoria della computabilità, disciplina che studia e classifica gli algoritmi in base a canoni
di complessità, cerca di definire e catalogare le regole affinché un problema generico possa
essere risolto con algoritmi, e possa quindi essere definito computabile. Questa teoria si è
posta una domanda alla quale, nel 1966, hanno dato risposta due matematici italiani, Corrado Böhm e Giuseppe Jacopini, formulando uno dei più importanti teoremi dell’informatica.
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
7
UdA 7
Il linguaggio C
La domanda è: Quali algoritmi sono codificabili con i tre costrutti concatenazione, selezione e iterazione?
La risposta è la seguente:
TEOREMA DI JACOPINI-BÖHM
Con i tre costrutti fondamentali, cioè concatenazione, selezione e iterazione, è possibile codificare tutti gli algoritmi computabili.
Da questo teorema possiamo ricavare due caratteristiche dei linguaggi, note come completezza ed equipotenza.
LINGUAGGIO COMPLETO
Un linguaggio di programmazione che ammette le tre figure strutturali fondamentali
permette di descrivere tutti gli algoritmi, e si definisce linguaggio completo.
Se con le tre figure fondamentali è possibile risolvere tutti gli algoritmi, ne deriva che tutti i
linguaggi che le ammettono possono risolvere tutti gli algoritmi, e sono quindi equipotenti.
EQUIPOTENZA
Due linguaggi sono equipotenti se ammettono le tre figure strutturali fondamentali.
■■ Loop infinito
L’istruzione iterativa è comunemente indicata con il termine inglese loop, cioè ciclo; è di
uso comune nello slang informatico il termine “looppare” che significa “rimanere dentro
un ciclo e ripetere l’iterazione”.
Nella terminologia dei programmatori ricorre anche l’espressione “sono in un loop infinito”, che è sinonimo di “non riesco a trovare la soluzione”.
Questo termine deriva proprio dal fatto che le istruzioni iterative possono provocare una
categoria di errori più gravi e insidiosi di quelli studiati finora: i cicli infiniti.
ESEMPIO
Algoritmo errato con loop infinito
Analizziamo come esempio il seguente segmento di codice, che verifica (in modo errato!)
se un numero è pari o dispari; come strategia prende il numero inserito dall’utente e continua a sottrargli due, fino a raggiungere il numero 0.
8
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
Il ciclo a condizione iniziale
Lezione 7
L’algoritmo non è completamente errato: infatti, finché vengono inseriti numeri pari, il
funzionamento è corretto. Eseguiamo la trace table per un numero dispari, per esempio 7.
Dal momento che la condizione (numLetto != 0) è sempre verificata, l’iterazione continua all’infinito; quella di mandare in esecuzione un programma e non ottenere risposta è
una situazione che si verifica spesso.
Il calcolatore continua a elaborare ma non succede niente e sullo schermo non compaiono
i risultati: siamo in presenza di un ciclo senza fine o loop infinito.
Il debugging può essere eseguito proprio come la trace table, cioè inserendo all’interno del
ciclo istruzioni di echo che visualizzino a ogni iterazione il contenuto delle variabili più significative, tra cui quella sulla quale vengono effettuati i controlli di iterazione.
Prova adesso!
• Utilizzare il ciclo while
• Correggere codice errato
APRI IL FILE infinito.c
Correggi la condizione del ciclo while affinché possa funzionare correttamente.
Confronta la tua soluzione con quella riportata nel file infinitoSol.c.
■■ Precedenza e associatività degli operatori
Riportiamo in una tabella riepilogativa le precedenze tra i vari operatori così come vengono valutate nelle espressioni aritmetiche e/o logiche.
OPERATORI
ASSOCIATIVITÀ
() [] -> .
da sinistra a destra
! - ++ -- + - * & (tipo) sizeof
da destra a sinistra
* / %
da sinistra a destra
+ -
da sinistra a destra
<< >>
da sinistra a destra
< <= > >= == !=
da sinistra a destra
&
da sinistra a destra
^
da sinistra a destra
|
da sinistra a destra
&&
da sinistra a destra
||
da sinistra a destra
?:
da destra a sinistra
= += -= *= /= %= &= |= <<= >>=
da destra a sinistra
,
da sinistra a destra
Gli operatori unari +, – e * hanno precedenza maggiore delle rispettive forme binarie.
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
9
UdA 7
Il linguaggio C
ABBIAMO IMPARATO CHE...
• •In alcune situazioni un’azione deve essere eseguita in modo ripetuto, in modo ciclico ( o
iterato), in base al valore di una istruzione di controllo, chiamata condizione di ingresso al
ciclo.
• Chiamiamo questa istruzione ciclo a condizione iniziale, ed ha la seguente struttura:
parola
chiave
condizione
inizio
blocco
corpo
del ciclo
fine
blocco
fine
istruzione
while
<condizione>
{
<istruzioni>
}
;
• Il ciclo prende anche nome di iterazione indeterminata, in quanto non è possibile sapere a
priori quante volte dovrà essere ripetuto.
• Con i tre costrutti fondamentali, cioè concatenazione, selezione e iterazione, è possibile
codificare tutti gli algoritmi computabili (teorema di Jacopini-Böhm).
10
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
Il ciclo a condizione iniziale
Lezione 7
Verifichiamo le competenze
conoscenze
1. Risposta multipla
1Indica qual è l’output di questo codice
inserendo rispettivamente: n1 = 3, n2 = 5.
int num;
scanf(“%d”,&num);
while(num>3)
{
printf(“ %d”,num);
num--;
}
n1:
a. 3
n2:
a. 4 3
b. 3 2 1
c. “ ”
d. 2 1
b. 5 4
c. 5 4 3 2 1
d. “ ”
2Indica qual è l’output di questo codice
inserendo rispettivamente: n1 = 4, n2 = 7, n3 = 0.
int num;
scanf(“%d”,&num);
while(num<10)
{
printf(“%d”,num);
num+=2;
}
n1:
a. 8
n2:
a. 911
n3:
a.02468
b. 468
c. 6810
d. 46810
b. 9
c. 79
d. 7911
b.2468
c.246810
3 Qual è l’output di questo codice?
int num,dato;
num=7;
dato=2;
while(num>0)
{
printf(“%d”,dato);
dato+=num;
num-=2;
}
a. 21417
b. 29147
c. 291417
d. 29117
4 Qual è l’output di questo codice?
int num,dato;
num=5;
dato=2;
while(num>3)
{
printf(“%d”,dato);
dato*=num;
num-=1;
}
a. 210
b. 2104
c. 21020
d. 21040
d.0246810
2. Vero o falso
1 Iterare significa ripetere ciclicamente un gruppo di istruzioni.
2 La condizione di ingresso è una condizione logica.
3 Nel ciclo a condizione iniziale il corpo viene eseguito almeno una volta.
4 Il corpo del ciclo deve essere sempre racchiuso tra { }.
5 Un contatore è una variabile che viene incrementata ripetutamente di un’unità.
6 Nel ciclo a condizione iniziale se il test dà esito VERO si ripete il corpo del ciclo.
7 Nel ciclo a condizione iniziale è noto a priori il numero delle iterazioni da eseguire.
8 Un accumulatore è una variabile che viene incrementata ripetutamente di un’unità.
9 Per verificare il corretto funzionamento di un ciclo si utilizza la tabella di traccia (o trace table).
10 Con la trace table si correggono gli errori presenti nel codice.
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
11
UdA 7
Il linguaggio C
Verifichiamo le competenze
1. Risposta aperta
Nei seguenti esercizi sono indicati alcuni segmenti di codice: in base ai valori assegnati alle variabili, annota i risultati
visualizzati sullo schermo oppure, se necessario, individua la presenza di errori.
1 Qual è l’output di questo codice?
int num,dato;
num=1;
dato=1;
while(num<6)
{
if(num/2==1)
printf(" %d",dato);
else
printf(" %d",dato-1);
dato+=num; //dato=dato+num;
num++;
//num=num+1;
}
2 Qual è l’output di questo codice?
int num,dato;
num=1;
dato=1;
while(num<10)
{
if(num/2==0)
printf(" %d",dato);
else
printf(" %d",dato-1);
dato=num-dato;
num+=2;
//num=num+2;
}
3 Qual è l’output di questo codice?
int num,dato;
num=1;
dato=1;
while(num<60)
{
if(num/2==0)
printf(" %d",dato);
else
printf(" %d",dato-1);
dato+=num; //dato=dato+num;
num+=dato; //num=num+dato;
}
4Correggi il codice in modo da visualizzare
13579.
num=5;
dato=1;
while(num>0)
{
printf(" %d",dato);
dato+=1;
//dato=dato+1;
num--;
//num=num-1;
}
5 Individua gli errori nel codice facendo in modo
che visualizzi i numeri pari compresi tra 10 e 20.
int num,dato;
num=1;
dato=10;
while(num<12)
{
printf(" %d",dato);
dato++;
//dato=dato+1;
num+=2;
//num=num+2;
}
6 Completa il codice in modo tale da visualizzare
la potenza del 2 fino a 25.
int num,dato;
num=1;
dato=1;
while(num<___)
{
printf(" %d",dato);
dato=dato*___;
num=num+___;
}
7 Correggi una sola istruzione in modo tale
da visualizzare la potenza del 3 fino a 34.
int num,dato;
num=1;
dato=1;
while(num<90)
{
printf("\n %d",dato);
num=dato*3;
dato=dato+num;
}
int num,dato;
12
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
Il ciclo a condizione iniziale
Lezione 7
2. Esercizi
Progetta e realizza completamente in linguaggio di programmazione il codice che risolva i problemi proposti.
1 Scrivi un programma che legge un numero num e quindi successivamente esegue la somma di num
numeri inseriti dall’utente.
2 Scrivi un programma che legge 10 numeri e ne stampa il massimo.
3 Scrivi un programma che legge un numero num e visualizza tutti i numeri pari inferiori a tale numero.
4 Scrivi un programma che esegue la somma di tutti i numeri multipli di 5 compresi tra 10 e 100.
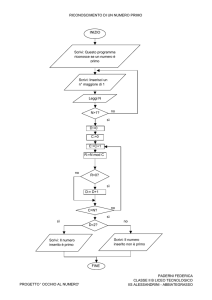
5 Scrivi un programma che legge un numero num e visualizza tutti i numeri primi inferiori a tale numero.
6 Scrivi un programma che visualizza i numeri pari multipli di 8 compresi tra 10 e 100.
7 Scrivi un programma che prende in ingresso un numero num e calcola il doppio della somma dei
primi num numeri.
8 Scrivi un programma che chiede in ingresso un numero finché non si inserisce un numero dispari.
Quando questo avviene, il programma termina scrivendo quanti numeri pari erano stati inseriti in
precedenza.
9 Scrivi un programma che legge una sequenza di numeri interi positivi terminanti con l’immissione
del numero 0 e ne ricerca il valore minimo visualizzandolo sullo schermo.
10 Scrivi un programma che esegue la moltiplicazione di due numeri inseriti da un utente utilizzando il
metodo delle somme successive.
11 Scrivi un programma che legge un numero num ed esegui il calcolo della somma dei primi num
numeri interi positivi pari.
12 Scrivi un programma che legge un numero num e visualizza sullo schermo tutti i suoi fattori.
13 Scrivi un programma che legge una serie di numeri interi positivi arrestandosi quando la somma dei
numeri immessi supera un valore costante letto come primo numero della sequenza.
14 Scrivi un programma che legge da tastiera una sequenza di lunghezza ignota a priori di numeri interi
positivi. Il programma, a partire dal primo numero introdotto, stampa ogni volta la media di tutti i
numeri introdotti. Termina quando il numero inserito è negativo.
15 Scrivi un programma che legge da tastiera una sequenza di numeri positivi e a ogni numero letto
ne stampa la somma progressiva. Il programma termina quando si introduce un numero minore o
uguale a zero.
16 Scrivi un programma che verifica se l’anno è bisestile: l’utente inserisce un anno e il calcolatore
verifica se è bisestile. Se l’utente inserisce un numero minore di 0 il programma termina (senza
ovviamente fare alcuna verifica); altrimenti, al termine della verifica, si ricomincia da capo (un anno
è bisestile se è divisibile per 4 ma non per 100, oppure se è divisibile per 400).
17 Scrivi un programma che ricerca i primi tre numeri perfetti e li visualizza sullo schermo (un numero è
perfetto se è uguale alla somma dei suoi divisori, per esempio il numero 6 è perfetto dato che 6 =
1 + 2 + 3).
18 Scrivi un programma che esegue il calcolo del fattoriale di un numero num inserito (il fattoriale di un
numero si ottiene moltiplicando il numero per tutti i suoi predecessori: per esempio, il fattoriale di 5
è dato da 5*4*3*2*1 e si indica con 5!).
19 Ricerca i primi due numeri amicabili e visualizzali sullo schermo: la definizione di numero amicabile
è attribuita a Fermat, e afferma che sono amicabili le coppie di numeri tali che ogni numero è la
somma dei divisori dell’altro numero (per esempio 17.296 e 18.416).
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
13
UdA 7
Il linguaggio C
Esercizi
Verifichiamo
per ille
recupero
competenze
Strutture di controllo, cicli e tipi semplici
1 Calcolo del fattoriale di un numero
Quante volte viene eseguita l’operazione di stampa nel seguente programma?
main()
{
int i;
i = 5;
while (i>=0)
printf(“Il valore di i e`: %d\n”, i);
}
2 Ciclo while
Si considerino i seguenti due esempi:
….
int a;
…
a = 12;
while(a<10)
a++;
…
….
int a;
…
a = 12;
while(a>10)
a++;
…
Quante volte vengono eseguite le istruzioni nel corpo di ciascuno dei due while?
3 Da binario a decimale
Scrivi un programma che converte un numero binario in decimale.
4 Calcolo del valore medio
Scrivere un programma C che richiede all’utente l’inserimento di una serie di numeri interi (l’acquisizione termina
quando l’utente inserisce il valore 0) e stampa la somma dei numeri compresi tra 10 e 20 estremi inclusi (se non
ce ne sono il programma stampa 0).
Ad esempio, se l’utente inserisce la sequenza
7, 25, 13, 10, 20, 70, 0
il programma termina stampando 43.
5 Cosa risulta?
Determinare il valore visualizzato dai seguenti programma nel caso in cui num=4 e per i seguenti valori della
variabile conta: conta=5, conta=0, conta=1, conta=–5.
int conta, num;
scanf(“%d”, &conta);
14
scanf(“%d”, &num);
while (conta != 0)
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
Il ciclo a condizione iniziale
{
num = num * 10;
conta = conta - 1;
}
printf(“%d\n”, num) ;
int conta, num;
scanf(“%d”, &conta);
Lezione 7
scanf(“%d”, &num);
while (conta > 0)
{
num = num * 10;
conta = conta - 1;
}
printf(“%d\n”, num) ;
6 Numeri maggiori di 0
Si scriva un programma C (ed il relativo diagramma a blocchi) che legge da tastiera una sequenza di 10 numeri
interi e, al termine, stampa a video il numero dei numeri letti che sono maggiori di zero, di quelli che sono minori
di zero e di quelli nulli.
7 Calcolo del fattoriale di un numero
Scrivi un programma che acquisisce da tastiera un numero e ne calcola il fattoriale. Si ricorda che le regola di
calcolo è la seguente:
n! = n*(n-1)! se n > 1
n! = 1 se n è pari a 0 oppure 1
8 Verifica numeri primi
Scrivi un programma che decide se un numero dato dall’utente è primo oppure no. Si ricorda che un numero si
dice primo se non è divisibile per nessuno dei valori compresi tra il numero stesso e 1. Si definisca il diagramma a
blocchi prima di procedere alla scrittura del codice.
9 Calcolo del minimo e del massimo
a) Si legga una sequenza di numeri interi e se ne stampi il valore massimo.
Ci si basi sulle ipotesi seguenti:
−− il valore di ciascun elemento appartenente alla sequenza è > 0 e < 100
−− non si conosce a priori il numero degli elementi appartenenti alla sequenza
−− la fase di acquisizione termina quando viene letto il “terminatore” (valore 999).
−− la sequenza potrebbe essere vuota.
b) Si consideri il problema del punto a) e si formuli una soluzione, stavolta ipotizzando che il numero
di elementi della sequenza di ingresso sia sempre pari a 10.
10 Calcolo del valore medio 1
Si legga una sequenza di numeri interi e se ne stampi il valore medio.
Le ipotesi sono:
−− il valore di ciascun elemento appartenente alla sequenza è > 0 e < 100
−− non si conosce a priori il numero degli elementi appartenenti alla sequenza
−− la fase di acquisizione termina quando viene letto il “terminatore” (valore 999)
−− la sequenza potrebbe essere vuota.
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
15
UdA 7
Il linguaggio C
11 Ricerca del numero 0
Si legga una sequenza di numeri interi. Ogni volta che viene letto il valore 0, si stampi la frase “ho letto uno 0”. Se
nella sequenza letta non è contenuto neppure uno 0, si stampi la frase “non ho trovato nessuno 0”.
Le ipotesi sono:
−− il valore di ciascun elemento appartenente alla sequenza è maggiore o uguale a 0 e < 100
−− non si conosce a priori il numero degli elementi appartenenti alla sequenza
−− la fase di acquisizione termina quando viene letto il “terminatore” (valore 999)
12 Calcolo del prodotto di due numeri per somme
Si leggano due numeri interi di valore maggiore o uguale a 0 e si stampi il prodotto dei due numeri letti calcolato
per somme successive. Si ottimizzi l’esecuzione del ciclo di calcolo.
13 Radice quadrata
Scrivi un programma che calcola la radice quadrata di un intero (per eccesso).
14 Numero palindromo
Scrivi un programma per verificare se un numero è palindromo
15 Da binario a decimale
Scrivi un programma per converte un numero binario in decimale
16 Elabora numeri dispari
Scrivi un programma che somma e moltiplica numeri dispari fino ad un valore inserito dall’utente.
17 Elabora cifre di un numero
Scrivi un programma che somma e moltiplica tra loro le singole cifre di un numero
18 Elabora sequenza di numeri
Scrivi un programma che legga una serie di valori interi (terminata dal valore 0), e che restituisca in output la
somma, il valor medio, il massimo e il minimo dei valori letti (escludendo dal computo il valore 0 che termina la
serie). Compilare il codice sorgente per ottenere un file eseguibile con nome Serie.
Consiglio: Prevedere il caso della sequenza vuota (attenti alla divisione per 0!).
19 Ricerca valori minimi
Scrivi un programma in linguaggio C che, ricevendo in ingresso una sequenza di lunghezza arbitraria di almeno
due numeri interi diversi da zero, terminata da uno zero, produca in uscita i due valori minimi letti in ingresso
(escluso l’ultimo zero).
Ad esempio, ricevendo in ingresso la sequenza
7 2 19 4 45 3 7 9 3 0
produce in uscita 2 3
Altro esempio: ricevendo in ingresso la sequenza
7 2 19 4 2 3 7 9 3 0
produce in uscita 2 2
16
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
Il ciclo a condizione iniziale
Lezione 7
20 Ricerca del numero dei numeri
Scrivi un programma che riceva in ingresso un numero positivo N e determini il massimo intero K tale che la
somma dei primi K interi sia minore o uguale a N.
Ad esempio, se N=20 allora K risulta 5, infatti
1 + 2 + 3 + 4 + 5 = 15
mentre
1 + 2 + 3 + 4 + 5 + 6 = 21
Esercizi per l’approfondimento
1 Ricerca di tre elementi contigui
Scrivere un programma C che, ricevendo in ingresso una sequenza di lunghezza arbitraria di numeri interi diversi
da zero, terminata da uno zero, produca in uscita la sequenza di tre elementi contigui la cui somma è massima (se
sono presenti più sequenze con somma massima, è sufficiente stampare la prima).
Per semplicità, si assuma che la sequenza inserita comprenda almeno tre numeri interi oltre lo zero.
Ad esempio, se l’utente inserisce la sequenza
7, 2, 19, 4, 45, 3, 7, 9, 3, 0
il programma termina e stampa 19, 4, 45.
2 Conversione Binario-Decimale
Scrivi un programma in linguaggio C che converta un numero binario in un numero decimale. Il numero binario è
rappresentato su N bit, e il valore di N è inserito da tastiera.
L’utente inserisce le cifre del numero binario un bit alla volta, partendo dal bit meno significativo (ossia dal bit di
peso 20). Il programma visualizzerà il numero decimale corrispondente.
Suggerimento.
Per calcolare le potenze di 2 utilizzare la funzione pow, includendo la libreria math.h.
Ad esempio per calcolare 25, si scriverà pow(2,5). In generale, data una base a, per calcolare y = ab, si scrive y =
pow(a,b) includendo la libreria math.h.
3 Ascii modificati
Si scriva un programma che acquisisce una sequenza di caratteri dallo standard input e restituisce sullo standard
output la sequenza codificata. La codifica viene effettuata sostituendo a ciascun carattere alfabetico il carattere
successivo nella tabella ASCII.
4Fibonacci
Scrivere un programma che, ricevuto in ingresso un intero N≥0, calcoli l’N-simo elemento della sequenza F dei
numeri di Fibonacci, definita così:
F(0) = 0
F(1) = 1
F(K) = F(K-1)+F(K-2) per K≥2
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
17
UdA 7
Il linguaggio C
In altre parole, la sequenza dei numeri di Fibonacci è la seguente:
0, 1, 1, 2, 3, 5, 8, 13, …
in cui ciascun numero, dal terzo in poi, è la somma dei due che lo precedono.
5 Numeri primi
Scrivere un programma che, ricevuto in ingresso un intero strettamente maggiore di 0, determini se tale numero
è primo.
6 Gioco dei dadi
Scrivere un programma che, ricevuto in ingresso un intero strettamente maggiore di 0, determini se tale numero
è primo.
Si consideri il seguente ipotetico gioco d’azzardo ai dadi cui partecipa un solo giocatore. All’inizio del gioco, il
giocatore ha a disposizione 1000 euro. Il giocatore immette una puntata (che non può essere superiore al saldo
disponibile) e tira due dadi: se il punteggio supera 6 il giocatore vince la puntata (essa viene quindi sommata al
saldo disponibile del giocatore) se invece il punteggio va da 1 a 6 il giocatore perde la puntata (essa viene quindi
sottratta al saldo disponibile del giocatore). Il gioco finisce quando il giocatore si ritira oppure quando il saldo
arriva a zero. Il giocatore può ritirarsi solo se ha puntato (anche in più giocate) almeno 300 euro.
Il programma deve simulare il gioco descritto. In particolare:
−− ad ogni iterazione, il programma deve chiedere al giocatore di immettere una puntata e acquisirla, ripetendo
l’acquisizione se la puntata supera strettamente il saldo disponibile.
−− il programma chiede quindi il punteggio ottenuto dal lancio dei dadi, ripetendo l’acquisizione se il numero non
è compreso tra 2 e 12: dopo ogni lancio dei dadi, il programma deve avvisare il giocatore del fatto di aver vinto
o perso, quindi deve stampare il nuovo saldo disponibile.
−− il programma, prima di cominciare una nuova iterazione, deve chiedere al giocatore se desidera continuare, ma
solo se il giocatore ha puntato almeno 300 euro.
−− il programma termina se il saldo arriva a 0.
7 Macchina del caffè
Si sviluppi un programma in linguaggio C che, come nel caso di una macchina distributrice di caffè, riceve in
ingresso un numero intero positivo N (corrispondente ad un importo da pagare in centesimi) e, successivamente,
una sequenza di numeri interi corrispondenti alle monete inserite, che possono essere da 1, 5, 10, 20 e 50
centesimi.
Il programma deve ripetere l’acquisizione di ciascun numero se non corrisponde ad una moneta tra quelle indicate.
Appena l’importo richiesto N viene raggiunto o superato, il programma interrompe l’acquisizione della sequenza
e restituisce una serie di numeri interi corrispondenti al resto in monete da 1 e 5 centesimi.
Ad esempio, se il programma riceve N=101 e la sequenza 50, 20, 20, 20, produce in uscita 5, 1, 1, 1, 1
Esercizi riepilogativi
1 Scrivi un programma che, data in input una stringa di (al massimo) 100 caratteri, conti quante volta
compare il carattere ‘a’.
2 Scrivi un programma che, data in input una stringa di (al massimo) 100 caratteri, conti quante volta
compare la sequenza ‘ab’.
18
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
Il ciclo a condizione iniziale
Lezione 7
3 Scrivi un programma in linguaggio C che, come nel caso di una macchina distributrice di caffè, riceve
in ingresso un numero intero positivo N (corrispondente ad un importo da pagare in centesimi) e,
successivamente, una sequenza di numeri interi corrispondenti alle monete inserite, che possono
essere da 1, 5, 10, 20 e 50 centesimi.
Il programma deve ripetere l’acquisizione di ciascun numero se non corrisponde ad una moneta tra
quelle indicate. Appena l’importo richiesto N viene raggiunto o superato, il programma interrompe
l’acquisizione della sequenza e restituisce una serie di numeri interi corrispondenti al resto in monete
da 1 e 5 centesimi.
Ad esempio, se il programma riceve N=101 e la sequenza 50, 20, 20, 20, produce in uscita 5, 1, 1, 1, 1
almeno due numeri interi diversi da zero, terminata da uno zero, produca in uscita i due valori minimi
letti in ingresso (escluso l’ultimo zero).
Ad esempio, ricevendo in ingresso la sequenza
7 2 19 4 45 3 7 9 3 0
produce in uscita 2 3
Altro esempio: ricevendo in ingresso la sequenza
7 2 19 4 2 3 7 9 3 0
produce in uscita 2 2
che la somma dei primi K interi sia minore o uguale a N.
Ad esempio, se N=20 allora K risulta 5, infatti
1 + 2 + 3 + 4 + 5 = 15 mentre
1 + 2 + 3 + 4 + 5 + 6 = 21
4 Scrivi un programma in linguaggio C che, ricevendo in ingresso una sequenza di lunghezza arbitraria di
5 Scrivi un programma che riceva in ingresso un numero positivo N e determini il massimo intero K tale
6 Scrivi un programma C che, ricevendo in ingresso una sequenza di lunghezza arbitraria di numeri
interi diversi da zero, terminata da uno zero, produca in uscita la sequenza di tre elementi contigui la
cui somma è massima (se sono presenti più sequenze con somma massima, è sufficiente stampare la
prima).
Per semplicità, si assuma che la sequenza inserita comprenda almeno tre numeri interi oltre lo zero.
Ad esempio, se l’utente inserisce la sequenza
7, 2, 19, 4, 45, 3, 7, 9, 3, 0
il programma termina e stampa 19, 4, 45.
7 Scrivi un programma che, ricevuto in ingresso un intero N≥0, calcoli l’N-simo elemento della sequenza
F dei numeri di Fibonacci, definita così:
F(0) = 0
F(1) = 1
F(K) = F(K-1)+F(K-2) per K≥2
In altre parole, la sequenza dei numeri di Fibonacci è la seguente:
0, 1, 1, 2, 3, 5, 8, 13, …
in cui ciascun numero, dal terzo in poi, è la somma dei due che lo precedono.
P. Camagni, R. Nikolassy, TI Professional Office 2010 e Windows 7, Nuova Edizione OPENSCHOOL, © Ulrico Hoepli Editore S.p.A. 2014
19