Integrazione numerica di Simpson - Sito Personale di Ettore Limoli

Lezioni di matematica
Integrazione numerica di Simpson
Prof. Ettore Limoli
Metodi di integrazione numerica
La formula di Bézout o dei trapezi è una formula di quadratura mediante interpolazione lineare della
funzione. Le formule di Cavalieri-Simpson sono formule di quadratura mediante interpolazione polinomiale.
In altre parole, all’andamento di una funzione y = f(x), nell’intervallo di integrazione [a, b] si sostituisce una
funzione polinomiale. Se la funzione è di primo grado (retta) si ha la formula dei trapezi o di Bézout, se è di
grado maggiore a uno si ha una formula di Cavalieri-Simpson.
Figura 1
Figura 2
1
Un caso semplice di formula di Cavalieri-Simpson è quello in cui interpoliamo tramite una funzione
polinomiale di secondo grado (parabola).
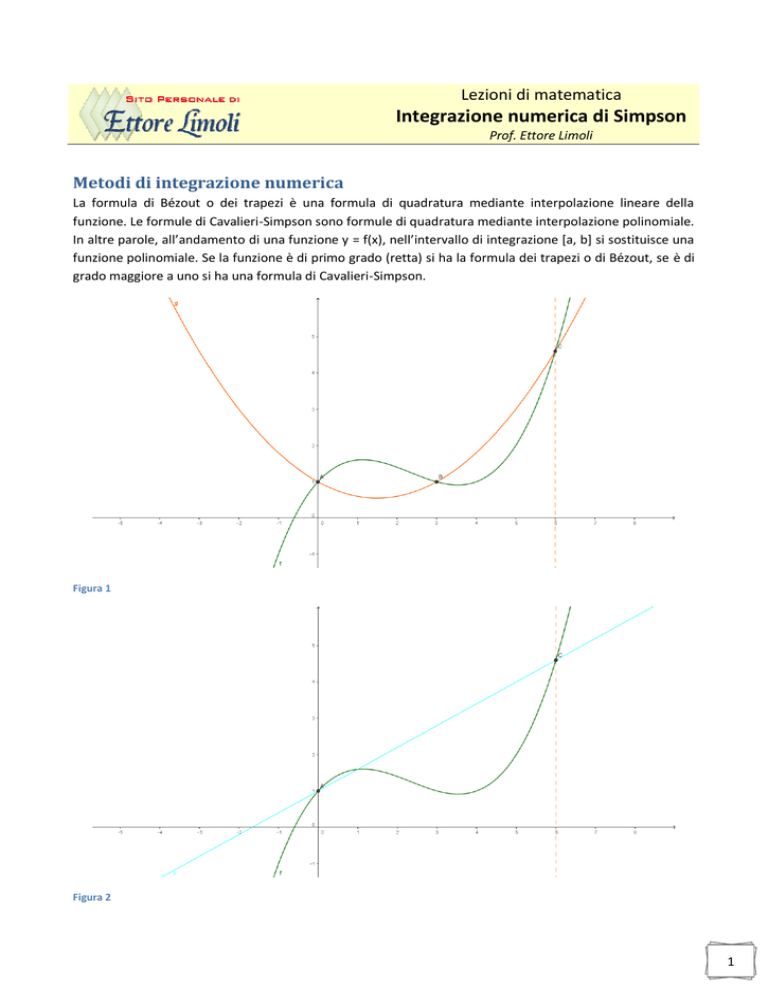
In Figura 1 si vede come la parabola g, passante per i punti A, B, C (con B punto medio di AC), approssimi
meglio l’andamento della funzione f di quanto non faccia la retta AC (interpolazione lineare) mostrata in
Figura 2. Le aree, delimitate dalla f e dalla g nei tratti tra A e B e tra B e C, grossomodo, si equivalgono.
Lo stesso non si può dire per la retta AC (interpolazione lineare) che con le sue intersezioni con la f
determina due regioni di piano di area palesemente differente.
Chiaramente, più è piccolo l’intervallo tra i punti A e C tanto è più piccolo l’errore che si commette
sostituendo all’integrale della f l’integrale della g.
Formula del terzo di Simpson
È il caso più semplice delle formule del tipo Cavalieri-Simpson. Questa formula è comunemente detta del
terzo di Simpson perché in essa figura il fattore 1/3.
𝑏
Per determinare una stima dell’integrale ∫𝑎 𝑓(𝑥)𝑑𝑥 , dividiamo l’intervallo [a, b] in un numero pari n di
sottointervalli di ampiezza ℎ =
𝑏−𝑎
𝑛
mediante i punti di suddivisione xi = a + i  h, con i =0, 1, 2,…, n.
Consideriamo poi gli intervalli del tipo [x2i, x2(i+1)], con i =0, 1,…, n/2-1, e procediamo con l’interpolazione in
detti intervalli con la parabola g(x) passante per i tre punti: x2i , x2i+1 , x2(i+1).
Poniamo, per i=1,…,n/2:
𝑥2𝑖
𝐽𝑖 = ∫
𝑔(𝑥)𝑑𝑥
𝑥2(𝑖−1)
Avremo quindi:
𝑏
∫ 𝑓(𝑥) 𝑑𝑥 ≈ ∑
𝑎
𝑛
2
𝑖=1
𝐽𝑖
Consideriamo il primo di detti intervalli [x0, x2] e la parabola passante per i tre punti x0, x1, x2 del tipo:
𝑦 = 𝐴(𝑥 − 𝑥1 )2 + 𝐵(𝑥 − 𝑥1 ) + 𝐶
Imponiamo che passi per i tre punti (x0, y0), (x1, y1), (x2, y2), dove: yi = f(xi). Si ha, quindi:
𝑦0 = 𝐴(𝑥0 − 𝑥1 )2 + 𝐵(𝑥0 − 𝑥1 ) + 𝐶
{𝑦1 = 𝐶
𝑦2 = 𝐴(𝑥2 − 𝑥1 )2 + 𝐵(𝑥2 − 𝑥1 ) + 𝐶
Ricordando che gli intervalli sono di ampiezza h, si ha:
𝑦0 = 𝐴(−ℎ)2 + 𝐵(−ℎ) + 𝐶
{𝑦1 = 𝐶
𝑦2 = 𝐴(ℎ)2 + 𝐵(ℎ) + 𝐶
2
La soluzione è:
𝑦0 + 𝑦2 − 2𝑦1
2ℎ2
𝑦2 − 𝑦0
𝐵=
2ℎ
{𝐶 = 𝑦1
𝐴=
Inoltre
𝑥
𝑥2
∫ [𝐴(𝑥 − 𝑥1
)2
𝑥0
2
(𝑥 − 𝑥1 )3
(𝑥 − 𝑥1 )2
2
+ 𝐵(𝑥 − 𝑥1 ) + 𝐶] 𝑑𝑥 = [𝐴
+𝐵
+ 𝐶 𝑥] = 𝐴ℎ3 + 2 𝐶ℎ
3
2
3
𝑥
0
Sostituendo, si ricava:
𝐽1 =
ℎ
3
(𝑦0 + 4𝑦1 + 𝑦2 ).
Analogamente si ricavano gli altri valori di Ji .
In definitiva si ha:
𝑏
𝑛
2
𝑛
𝑛
ℎ
2
2 −1
∫ 𝑓(𝑥) 𝑑𝑥 ≈ ∑ 𝐽𝑖 = ∙ (𝑦0 + 4 ∑ 𝑦2𝑖−1 + 2 ∑ 𝑦2𝑖 + 𝑦𝑛 )
3
𝑖=1
𝑖=1
𝑖=1
𝑎
Esempio svolto con l’ausilio del foglio elettronico di calcolo
𝜋
Si voglia approssimare con la formula del terzo di Simpson ∫0 𝑠𝑒𝑛(𝑥)𝑑𝑥 che, com’è noto, vale 2.
Prepariamo il foglio come segue.
3
Dove sono stati assegnati i nomi
Le formule introdotte sono le seguenti
Come è possibile vedere, si ottiene una buona approssimazione anche con un valore di n = 20 non
eccessivamente alto.
Prof. Ettore Limoli
4