Fisica 2
Corso di Laurea in Informatica
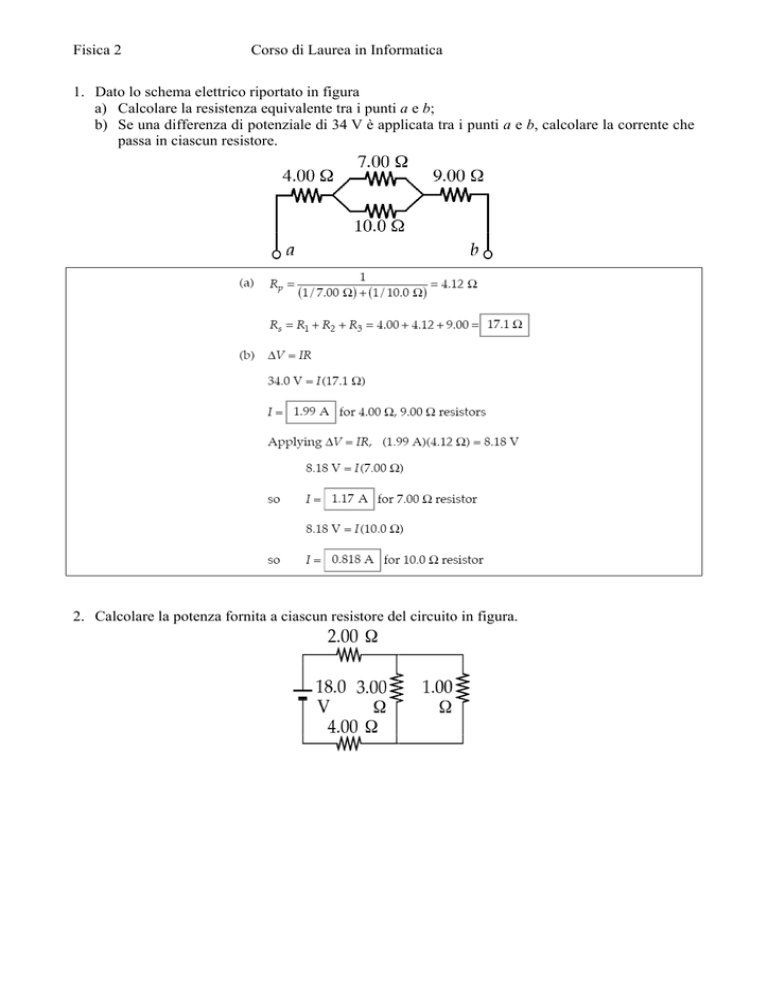
1. Dato lo schema elettrico riportato in figura
a) Calcolare la resistenza equivalente tra i punti a e b;
b) Se una differenza di potenziale di 34 V è applicata tra i punti a e b, calcolare la corrente che
passa in ciascun resistore.
2. Calcolare la potenza fornita a ciascun resistore del circuito in figura.
Fisica 2
Corso di Laurea in Informatica
3. Si consideri il circuito RC in figura, per il quale R=1 MΩ, C=5 μF, e ε=30 Volts. Determinare:
a) La costante di tempo del circuito
b) La carica massima sul condensatore dopo la chiusura dell’interruttore S
c) La corrente che circola in R dopo 10 sec dalla chiusura di S.
Fisica 2
Corso di Laurea in Informatica
4. Una batteria da 12 V è collegata in serie a un circuito con un resistore da 10.0 Ω e un induttore
da 2.0 H. Quanto tempo impiegherà la corrente per raggiungere il 50% del suo valore finale ?
Per un circuito serie
dovrà essere
5. Data la rete di condensatori in figura, si calcoli:
c) la capacità equivalente fra i punti (a) e (b);
d) la carica elettrica e la caduta di tensione sul condensatore da 20 μF, essendo
ΔVab=15.0 V
a
b
Fisica 2
Corso di Laurea in Informatica
6. Con riferimento al circuito in figura trovare: la corrente nel resistore da 20 Ω e la d.d.p. tra i
punti (a) e (b).
(Suggerimento: ruotare di 90º la figura)
Ruotiamo la figura.
Le resistenze da 20 e 5 Ω sono in serie, da cui
la fig. (b).
Le resistenze da 10, 5 e 25 Ω sono in
⎛
⎞
⎜
⎟
1
⎟ = 2.94 Ω , da cui la fig. (c).
parallelo Req = ⎜
⎜ 1 + 1 + 1 ⎟
⎜ 10 Ω 5 Ω 25 Ω ⎟
⎝
⎠
Le ultime due resistenze sono in serie, da cui
la fig. (d). La corrente che circola è pari a
ΔV
25V
=
= 1.93 A
I=
R 12.94 Ω
Con riferimento alla fig. (c) la d.d.p. ai capi
Della resistenza da 2.94 Ω è pari a
ΔV = I × R = 1.93 A × 2.94 Ω = 5.68V
Dalla figura (b) si può vedere che questa è uguale alla d.d.p. ai capi del parallelo di resistenze (da
10, 5 e 25 Ω) ed è la d.d.p. tra i punti a e b (risposta (b)). La corrente che circola nella resistenza
Fisica 2
Corso di Laurea in Informatica
da 20 Ω (fig. (a)) è la stessa di quella che circola nella resistenza da 25 Ω (fig. (b)), quindi
ΔV
5.68V
I = ab =
= 0.227 A
25 Ω
Rab
7. La figura mostra una vista dall’alto di una sbarretta metallica che può scivolare senza attrito su
due rotaie metalliche connesse ad una resistenza R da 6 Ω e distanti l =1.2 m. Il sistema è
immerso in un campo magnetico B=2.5 T diretto perpendicolarmente verso l’interno della
pagina. Considerando trascurabili i valori di resistenza elettrica della sbarretta e delle rotaie,
calcolare
a. La forza applicata Fapp necessaria per muovere la sbarretta verso destra alla velocità
costante di 2 m/s;
b. la potenza dissipata nel resistore.
a) La forza magnetica che agisce sulla sbarretta è pari in modulo a
FB = I A × B = I AB poichè deve essere I = ε R , essendo ε la f .e.m. indotta
( v velocità della sbarretta ) , si ha
2
2
BAv
B 2 A 2 v ( 2.5 T ) ⋅ (1.2 m ) ⋅ 2 m s
=
⋅ AB =
=
= 3.0 N
pari a ε = BAv
FB
R
R
6Ω
La forza da applicare Fapp deve essere quindi pari ad FB :
Fapp = FB = 3.0 N
La potenza dissipata nel resistore sarà
b)
B 2 A 2 v 2 ( 2.5 T ) ⋅ (1.2 m ) ⋅ ( 2 m s )
P=I R=
=
= 6.0W
R
6Ω
2
2
2
2
8. Un condensatore da 10 μF viene caricato con una batteria da 10 V attraverso una resistenza R.
Dopo 3 secondi dall’inizio della carica, il condensatore raggiunge una tensione di 4 V. Calcolare
il valore di R. (Suggerimento: utilizzare la legge di carica del condensatore)
La d .d . p. ai capi del condensatore segue la legge
ΔV ( t ) = ΔVmax (1 − e −t RC )
per t = 3sec sarà
− ( 3 s ) ( R⋅(10×10−6 F ) ) ⎤
⎡
4V = (10 V ) ⋅ ⎢1 − e
⎥⎦
⎣
0.4 = 1 − e
−
(
)
− 3×105 Ω R
3 ×105 Ω
= ln ( 0.6 )
R
e
(
) = 0.6
− 3×105 Ω R
⇒
R=−
3 ×105 Ω
= 587 k Ω
ln ( 0.6 )
9. Due condensatori, C1=25.0 μF e C2=5.0 μF, sono collegati in parallelo e caricati con una
Fisica 2
Corso di Laurea in Informatica
batteria da 100 Volts.
a) Disegnare il circuito e calcolare l’energia totale accumulata nei due condensatori;
b) Quale differenza di potenziale è necessaria ai capi dei due condensatori collegati in serie
affinché l’energia immagazzinata sia la stessa del caso (a) ? (Disegnare il circuito)
10. L’amperometro in figura segna una corrente di 2.0 A. Trovare le correnti I1 e I2 ed il valore di ε.
+
+
Fisica 2
Corso di Laurea in Informatica
11. Un elettrone dopo essere stato accelerato da una d.d.p. di 2400 V, entra in una regione in cui c’è
un campo magnetico uniforme di 1.70 T. Quanto valgono (a) il massimo e (b) il minimo valore
della forza magnetica a cui questa carica è sottoposta ?
In assenza di altre forze il protone si muove di moto circolare uniforme per c
quando v è parallelo o anti-parallelo a B
12. Un solenoide conduttore con 25 spire ha un diametro di 1.0 m. Esso è posto con il suo asse
lungo la direzione del campo magnetico terrestre di 50.0 μT, e quindi viene ruotato di 180° in
0.2 sec. Qual è la f.e.m. media che si genera ?
13. Si consideri il circuito in figura, dove C1=6 μF, C2=3 μF, V=20 Volts. Dapprima si carica C1
chiudendo l’interruttore S1. Poi S1 viene aperto, e il condensatore carico viene collegato a quello
scarico chiudendo l’interruttore S2. Calcolare
a) la carica iniziale di C1;
b) la carica finale di entrambi i condensatori.
a) Quando S1 è chiuso la carica su C1 sarà Q1 = C1 × V = ( 6 μ F ) × ( 20 V ) = 120 μ C .
b) Quando S1 è aperto ed S2 è chiuso, la carica totale rimarrà costante e si distribuirà tra i due
condensatori: Q1' = 120 μC − Q2' × V . La d.d.p. ai capi dei due condensatori sarà la stessa:
V′ =
Q1' Q2'
=
C1 C2
ovvero
120 μ C − Q2'
Q'
= 2 da cui Q2' = 40 μ C e Q1' = 80 μ C
6 μF
3μF
14. Una sbarretta metallica di 200 g che conduce una corrente di 10 A scivola su due binari
orizzontali distanti 0.5 m. Determinare l’intensità di un campo magnetico verticale necessario
per far sì che la sbarretta si muova a velocità costante. Il coefficiente di attrito dinamico tra il
binario e la sbarretta vale 0.1 .
Fisica 2
Corso di Laurea in Informatica
15. L’interruttore del circuito in figura viene chiuso all’istante t = 0. Trovare la corrente
nell’induttore e la corrente nell’interruttore (cioè in quel ramo del circuito) dopo 0.1 sec dalla
chiusura di S. (suggerimento: utilizzare le leggi di Kirchoff)
Utilizzando le leggi di Kirchoff al circuito:
dalle prime due
sostituendo nella terza
risolvendo l’eq. differenziale si avrà:
dopo 1 sec I3=0.5 A (1 – e-1) = 0.316 Ae
I1=1.5 A – 0.25 A e-1 = 1.408 A
Fisica 2
Corso di Laurea in Informatica
16. Determinare la corrente in ciascuno dei rami del circuito in figura.
+
+
Definiamo i versi arbitrari delle correnti e semplifichiamo le resistenze in serie:
legge delle correnti al nodo I 3 = I1 + I 2
⎧ I1 × 8 Ω − 4V − I 2 × 6 Ω = 0
legge delle maglie ( senso orario ) ⎨
sostituendo
⎩ 4 V − I 2 × 6 Ω − I 3 × 4 Ω − 12 V = 0
4V + I 2 × 6 Ω
⎧
I1 =
⎪
8Ω
I1 × 8 Ω − 4V − I 2 × 6 Ω = 0
⎧
⎪
⎨
⎨
⎩4 V − I 2 × 6 Ω − ( I1 + I 2 ) × 4 Ω − 12 V = 0 ⎪4V − I × 6 Ω − ⎛ 4V + I 2 × 6 Ω + I ⎞ × 4 Ω − 12 V = 0
⎜
2
2⎟
⎪⎩
8Ω
⎝
⎠
I 2 × 6 Ω − 2 V − I 2 × 7 Ω − 8V = 0 I 2 = −10 A
I1 = −7 A I 3 = −17 A
I versi sono opposti a quelli disegnati.
17. Un protone nello spazio interstellare possiede una energia pari a 10 MeV e percorre un’orbita
circolare di raggio R=5.8×1010 m (raggio dell’orbita di Mercurio intorno al Sole). Quanto vale il
campo magnetico in quella regione ?
(I valori della carica e della massa del protone
si trovano sul libro di testo)
In assenza di altre forze il protone si muove di moto circolare uniforme per cui deve essere
mv
B=
la velocità si ricava eguagliando l ' espressione dell ' energia cinetica
eR
1 2
2eV
all ' energia posseduta dal protone
mv = eV da cui v =
quindi
2
m
1
2 ×1.6727 × 10−27 kg ×107 V
m 2eV 1 2mV
=
=
= 7.88 × 10−12 T
5.8 × 1010 m
1.609 × 10−19 C
eR m
R
e
18. Si consideri il circuito RC in figura, per il quale R=1 MW, C1=2 μF, C2=3 μF e V=30 Volts.
B=
Fisica 2
Corso di Laurea in Informatica
Determinare:
a) La costante di tempo del circuito
b) La carica massima su ciascun condensatore dopo che l’interruttore S è stato chiuso per un
tempo sufficientemente
c) La corrente che circola in R dopo 10 sec dalla chiusura di S.
a) I condensatori in parallelo si comportano come un unico condensatore
C = C1 + C2 = 5 μ F
quindi τ = RC = 1×106 Ω × 5 ×10−6 F = 5sec
b) Dopo un tempo lungo entrambi i condensatori si " caricano " a 30 V
Q1 = C1V = 2 × 10−6 F × 30 V = 60 μ C Q2 = C2V = 3 ×10−6 F × 30 V = 90 μC
c) I = I iniz e −t τ =
V −t τ
30 V −10 s 5 s
e =
e
= 4.06 μ A
R
1× 106 Ω
19. Un induttore da 10 mH è percorso da una corrente I=Imaxsen(ωt), con =5 A e ω/2p=60 Hz.
Calcolare l’espressione di:
a) dipendenza dal tempo della f.e.m. autoindotta
b) dipendenza dal tempo dell’energia immagazzinata nell’induttore.
(mettere in relazione le dipendenze con l’andamento della corrente)
dI sin (ωt )
dI
= Lω I max cos (ωt ) =
a) ε autoindotta = L = L max
dt
dt
= 0.01 H × 120π sec−1× 5 A × cos (120π t ) ( sfasata di π 2 rispetto ad I )
1 2 1 2
LI = LI max sin 2 (ωt ) =
2
2
= 0.01 H × 25 A2 × sin 2 (120π t )
b) U B =
( frequenza doppia rispetto ad I )
20. Determinare il valore della capacità equivalente ai capi a e b.
−1
⎛1 1⎞
Cs = ⎜ + ⎟ μ F = 2.92 μ F
⎝5 7⎠
C p = ( 2.92 + 4 + 6 ) μ F = 12.92 μ F
21. È dato il sistema di condensatori mostrato nella figura. Si determinino le cariche su ciascun
Fisica 2
Corso di Laurea in Informatica
condensatore sapendo che ΔV=VA-VB=50 V. [Valori delle capacità dei condensatori: C1=1 μF;
C2=4 μF; C3= 8 μF; C4= 4 μF]
22. Si hanno due pile di f.e.m. ε = 1.5 V e resistenza interna r=0.1 Ω ciascuna, collegate tra loro in
serie e connesse ai capi di una resistenza R. Si determini il valore di R per cui la potenza
dissipata sul carico (cioè R) è massima. Calcolare anche Pmax. (Suggerimento: disegnare il
circuito e calcolare la corrente che attraversa il carico per determinare la potenza dissipata in
esso. Ricordarsi come si calcola il max di una funzione)
Fisica 2
Corso di Laurea in Informatica
2E
2r + R
2
⎛ 2E ⎞
2
La potenza dissipata sul carico vale P = i R = R ⎜
⎟
⎝ 2r + R ⎠
Risolvendo l’equazione della maglia si ricava i =
2
dP 4 E ( 2r − R )
=
= 0 da cui R = 2r = 0.2 Ω
Per trovare Pmax imponiamo
3
dR
( R + 2r )
2
Pmax
2
⎛ 2 × 1.5V ⎞
⎛ 2E ⎞
=i R=⎜
⎟ × 0.2 Ω = 11.25W
⎟ R=⎜
⎝ 2r + R ⎠
⎝ 0.2 Ω + 0.2 Ω ⎠
2
23. Prendendo in considerazione il circuito mostrato in figura si calcolino i valori delle correnti che
circolano in ciascuna delle resistenze, essendo V = 6V, R1 = 1Ω e R2 = R3 = R4 = 3Ω.
Il parallelo R234 =
1
= 1 Ω quindi la corrente erogata dal generatore vale
1
1
1
+ +
R2 R3 R4
V
= 3 A che è la corrente che circola in R1. Questa corrente si ripartisce nelle tre
R1 + R234
i
resistenze (uguali) R2, R3 e R4 e quindi i2 = i3 = i4 = = 0.33 A .
3
i=
24. Un filo rettilineo infinito è posto nello stesso piano di una spira conduttrice quadrata di lato a e
resistenza R. Inoltre, il filo è parallelo al lato del quadrato più vicino e posto ad una distanza a
da esso (vedi figura). Determinare il valore della potenza media dissipata nella spira quando il
filo è percorso da una corrente I=I0sen(ωt). (Suggerimento: rammentare la f.e.m. indotta da
variazioni di flusso del campo magnetico; il valor medio è dato dall’integrale sul periodo e
T
1
2
∫0 cos ωt dt = 2 ).
Fisica 2
Corso di Laurea in Informatica
a
I
a
a
Il campo magnetico generato dalla corrente nel filo vale B =
μ0 I
essendo r la distanza dal filo.
2π r
Il flusso del campo magnetico intercettato dalla spire vale
2a ⎛ μ I ⎞
μ Ia
2a
⎛ μ Ia ⎞
Φ B = ∫ B ( r ) dA = ∫ ⎜ 0 ⎟ a dr = ⎜ 0 ⎟ [ ln r ]a = 0 ln 2
a
2π
⎝ 2π r ⎠
⎝ 2π ⎠
d Φ B μ0 a ln 2 dI μ0 a ln 2
=
=
la f .e.m. indotta nella spira vale ε =
I 0ω cos ωt
dt
2π dt
2π
2
1 ⎛ μ a ln 2 ⎞
2
la potenza istantanea dissipata vale P =
= ⎜ 0
( I 0ω cos ωt )
⎟
R R ⎝ 2π ⎠
T
T
1
la potenza media Pm = ∫ P dt e ricordando che ∫ cos 2 ωt dt =
si ha
0
0
2
ε2
2
Pm =
1 ⎛ μ0 a ln 2 ⎞
1 ⎛ μ0 aI 0ω ln 2 ⎞
2 1
⎜
⎟ ( I 0ω ) =
⎜
⎟
2 2R ⎝
2π
R ⎝ 2π ⎠
⎠
2
25. Nel corso di un esperimento di effetto fotoelettrico, da una superficie metallica vengono estratti
elettroni aventi una velocità massima vmax = 4.6x105 m/s utilizzando una luce di lunghezza
d’onda λ = 625 nm.
a) Quento vale l’energia di estrazione della superficie ?
b) Qual è la frequenza di taglio per la stessa superficie ?
(Suggerimento: per semplificare i calcoli numerici si rammenta che hc=1240 ev·nm)
26. Un elettrone dopo essere stato accelerato da una d.d.p. di 2400 V, entra in una regione in cui c’è
un campo magnetico uniforme di 1.70 T. In funzione dell’orientamento del campo magnetico
quanto valgono (a) il massimo e (b) il minimo valore della forza magnetica a cui questa carica è
sottoposta ?
Fisica 2
Corso di Laurea in Informatica
In assenza di altre forze il protone si muove di moto circolare uniforme per c
quando v è parallelo o anti-parallelo a B
27. Con riferimento alla figura, il gruppo di elementi racchiusi dal riquadro tratteggiato
rappresentano l’indotto di un motore che presenta una resistenza di 7.5 Ω ed un’induttanza di
450 mH. Si assuma che la f.e.m. autoindotta nella bobina sia 10.0 V quando il motore gira alla
velocità normale (interruttore chiuso) con alimentazione a 12 V e con una resistenza R collegata
ai suoi capi. Calcolare il valore massimo di resistenza R necessario perchè la tensione ai capi
dell’indotto sia ≤ 80 V quando il motore viene scollegato (interruttore aperto). (Suggerimento:
considerare il circuito nei due casi interruttore chiuso ed interruttore appena aperto).
In condizioni normali (interruttore chiuso)
Appena si apre l’interruttore la corrente rimane al valore I=0.267 A, quindi
28. L’interruttore del circuito in figura viene chiuso al tempo t=0. Trovare l’andamento della
corrente nell’induttore e nell’interruttore in funzione del tempo. (Suggerimento: utilizzare le
leggi di Kirchoff assumendo le correnti come indicato in figura.)
Fisica 2
Corso di Laurea in Informatica
29. Un condensatore C1=6.0 μF viene caricato completamente da una batteria a 12 V e,
successivamente, disconnesso da essa. Viene quindi connesso ad un condensatore scarico
C2=3.0 μF come mostrato in figura. Quanto vale differenza di potenziale ai capi dei due
condensatori ? (Suggerimento: attenzione al tipo tipo di collegamento dei condensatori,
controllare come sono collegate le rispettive placche)
C1
C2
Inizialmente Q = C1V1 = 6 μ F ×12 V = 72 μ C.
Alla riconnessione, i condensatori sono in parallelo, quindi
V1′= V2′ = V e Q = Q1 + Q2 , sostituendo nella seconda si ha
V1C1 = VC1 + VC2 da cui V = V1
C1
6 μF
= 12 V
= 8V
C1 + C2
6 μF + 3μF
30. I condensatori di sintonizzazione utilizzati comunenemente negli apparecchi radio sono del tipo
a piatti sovrapposti: la capacità viene variata modificando l’area di sovrapposizione (vedi prima
figura). Se l’area di ciascun piatto è pari ad A e la distanza tra i singoli piatti è pari a d (il
dielettrico è aria), determinare la capacità massima dell’intero sistema schematizzato nella
seconda figura.
Il sistema è equivalente a 8 condensatori in parallelo, quindi Cmax = 8 C1 = 8
ε0 A
d
31. La velocità di un elettrone, emesso per effetto fotoelettrico da una lamina metallica illuminata
con una radiazione di lunghezza d’onda pari a 250 nm, risulta pari a 5.94×105 m/s. Determinare
l’energia di estrazione del metallo.
Fisica 2
Corso di Laurea in Informatica
L’energia cinetica del fotoelettrone emesso vale
2
2 m
1
1
K = mv 2 = × 9.11×10−31 kg × ( 5.94 ×105 ) 2 = 1.607 ×10−19 J = 1.00 eV
2
2
s
L’energia dei fotoni del fascio incidente vale
hc 6.626 ×10−34 J ⋅ s × 3 ×108 m s
E = hf =
=
= 7.951×10−19 J = 4.961 eV
250 × 10−9 m
λ
Quindi dalla relazione di Einstein K = hf − φ , si ha φ = hf − K = 4.961eV − 1.00 eV = 3.961 eV
32. Quanto vale la differenza di potenziale tra i punti X e Y del circuito in figura ? (Suggerimento:
sfruttare la simmetria dei due rami esterni del circuito.)
Risolvendo il parallelo RP =
6Ω ⋅12Ω
= 4Ω
18Ω
Poichè i rami esterni sono identici, deve essere I1=I2, quindi
8V-2I1-2V-3I1-4I3=0
e al nodo 2I1=I3 , risolvendo
I1=0.46 A e
I2=0.92 A
quindi VXY=8V - 4×0.92V=4.3 V
33. Sia dato il circuito RL serie con L=4.00 H e R=5.00 W, alimentato da una batteria da 22 V.
All’istante t=0 viene chiuso l’interruttore:
a) quale energia viene immagazzinata nell’induttore quando I=0.5 A ?
b) con quale rapidità viene immagazzinata l’energia (cioè la potenza) nell’induttore quando
I=1.00 A ?
c) quale potenza viene fornita dalla batteria al circuito quando I=5.00 A ?
Fisica 2
Corso di Laurea in Informatica
(b) quando I=1.0 A la legge di Kirchoff alla maglia prevede
la potenza immagazzinata nell’induttore è
(c) la potenza erogata dalla batteria al circuito per I=0.5 A vale
34. Una resistenza filiforme di sezione S = 1 mm2 è costituita dall'unione di un filo di lunghezza
l1 = 10 mm e resistività ρ1 = 5 × 10-5 Ωm con un filo di lunghezza l2 = 5 mm e resistività ρ2 =
3ρ1. Quando la resistenza è attraversata da una corrente uniforme I = 5 A calcolare:
a) i campi elettrici nei due materiali
b) la differenza di potenziale ai capi della resistenza
c) la carica presente sulla superficie di separazione dei due materiali.
a)
b)
c)
35. Una lampadina di potenza elettrica 40 W emette fotoni di lunghezza d’onda λ=582 nm. Tenuto
conto che solo il 5% della potenza elettrica viene trasformato in radiazione, calcolare il numero
di fotoni emessi al secondo.
Fisica 2
Corso di Laurea in Informatica
L’energia cinetica di un fotone vale
m⎞
⎛
6.63 × 10−34 J ⋅ s ) ⎜ 3.0 × 108 ⎟
(
hc
s⎠
⎝
=
= 3.4175 × 10−19 J
E=
−9
λ
582 × 10 m
La potenza luminosa emessa vale P = 5% × 40 W = 2 W = 2
J
s
Il numero di fotoni emessi sarà
J
2
P
fotoni
s
N fot = tot =
= 5.9 × 1018
J
E fot 3.4175 ×10−19
s
fotone
36. Si consideri il circuito mostrato in figura. Si determini:
a) La corrente totale erogata dalla batteria;
b) La potenza elettrica dissipata nel circuito;
c) La d.d.p. ai capi delle varie resistenze.
Si assuma R1=10 W, R2=10 W, R3= 5 W, R4=5 W, R5=20 W e V0 =30 V.
37. Un motore è collegato alla batteria di alimentazione tramite un cavo di rame (resistività
ρ = 1.69×10-8 Ω·m e densità di elettroni n = 8.49×1028 elettroni/m3) di diametro d = 5 mm e
lunghezza ℓ = 1 m. Calcolare il tempo impiegato da un elettrone per andare dalla batteria al
motore quando circola una corrente I = 100 A.
La densità di corrente che circola nel filo vale
I
4I
4 ×100 A
A
J= =
=
= 5.1
2
2
S πd
mm 2
π × ( 5 mm )
La velocità con cui si spostano gli elettroni nel filo è
C
5.1
j
mm
s ⋅ mm 2
=
= 0.38
vd =
elettroni
ne 8.49 ×1028
s
×1.602 ×10−19 C
m3
Il tempo impiegato a percorrere la distanza ℓ sarà
A 1000 mm
t= =
44 s
vd 0.38 mm
s
38. Sia dato il sistema di condensatori in figura (partitore di tensione capacitivo). Essendo V=300 V,
si determinino i valori di capacità dei tre condensatori se si vuole avere V1=3V3, V2=2V3 e
dovendo mantenere la capacità complessiva del sistema pari a C=300 nF.
Fisica 2
Corso di Laurea in Informatica
39. Sulla base del principio di esclusione di Pauli, elencare le possibili configurazioni dei numeri
quantici di un elettrone nei sottostrati 3d e 3p.
elettrone 3d : n=3 ℓ=2, totale 10 stati
elettrone 3p : n=3 ℓ=2, totale 6 stati
40. Con riferimento alla figura un raggio di luce incide normalmente sulla faccia ab di un prisma di
vetro (n=1.52). Trovare il massimo valore dell’angolo φ per il quale il raggio possa essere
totalmente riflesso dalla faccia ac, quando il prisma si trova in acqua (nacqua=1.33).
a
b
φ
c
L’angolo di incidenza sulla superficie a-c vale 90º-φ e la condizione di riflessione totale vale
⎛n ⎞
⎛ 1.33 ⎞
D
quindi nv sen ( 90D − φ ) = na ovvero nv cos (φ ) = na da cui φ = cos −1 ⎜ a ⎟ = cos −1 ⎜
⎟ = 28.9
⎝ 1.52 ⎠
⎝ nv ⎠
41. Il potenziale d’arresto per fotoelettroni emessi da una superficie investita da luce di lunghezza
d’onda di 491 nm è di 0.710 eV. Cambiando la lunghezza d’onda della luce incidente, si misura
un potenziale d’arresto di 1.43 V. Determinare il valore della nuova lunghezza d’onda.
Fisica 2
Corso di Laurea in Informatica
In entrambi gli esperimenti valgono le relazioni
⎧ hc
⎪ λ = Φ + K1
⎪ 1
essendo K1 = 0.71eV , K 2 = 1.43 eV e λ1 = 491 nm
⎨
⎪ hc = Φ + K
2
⎪⎩ λ2
Φ è lo stesso in entrambi i casi e, sostituendolo nella sec ond espressione .
hc hc
=
− K1 + K 2 da cui
λ2
λ1
λ2 =
(1240 eV ⋅ nm ) × ( 491 nm )
hcλ1
= 382 nm
=
hc + λ1 ( K 2 − K1 ) 1240 eV ⋅ nm + ( 491 nm ) (1.43 eV − 0.71 eV )
42. Con riferimento alla figura, un raggio di luce si propaga in aria e incide su un blocco di plastica
con un angolo θ1 =45° emergendone dalla faccia inferiore con un angolo θ2 =76° . Determinare
il valore dell’indice di rifrazione della plastica.
Alla prima superficie
1 ⋅ sen ( 45D ) = n ⋅ sen (α )
Alla seconda superficie
n ⋅ sen ( 90D − α ) = 1 ⋅ sen ( 76D )
ovvero
n ⋅ cos (α ) = 1 ⋅ sen ( 76D )
dividendo I e III espressione
tan (α ) =
sen ( 45D )
sen ( 76D )
= 0.729
α = 36.1
D
n=
sen ( 45D )
sen ( 36.1D )
= 1.2
43. L’indeterminazione nella posizione di un elettrone è stimata in 50×10-12 m, dell’ordine del
raggio dell’atomo d’idrogeno. Quale sarà l’indeterminazione minima nella misura della sua
quantità di moto ?
=
Sulla base del principio di indeterminazione di Heisenberg Δx Δp ≥ .
2
−34
=
1.05 ×10 J ⋅ s
kg ⋅ m
da cui Δp ≥
=
= 1.05 × 10−24
−12
s
2Δx 2 × 50 × 10 m
44. Calcolare l’energia immagazzinata nel condensatore C3 dopo aver chiuso l’interruttore ed atteso
un tempo molto lungo.
Fisica 2
Corso di Laurea in Informatica
La capacità equivalente C23 vale C23 =
C2 ⋅ C3
= 4 μF
C2 + C3
da cui Q23 = C23V = 4 μ F ×12 V = 48 μ C
1 Q232 1 ( 48 μ C )
quindi E3 =
=
= 96 μ J
2 C3 2 12 μ F
2
45. È dato il sistema di condensatori mostrato nella figura. Si determinino le cariche su ciascun
condensatore sapendo che ΔV=VA-VB=50 V. [Valori delle capacità dei condensatori: C1=1 μF;
C2=4 μF; C3= 8 μF; C4= 4 μF]
Fisica 2
Corso di Laurea in Informatica
46. Si consideri il circuito riportato in figura. I resistori R2 ed R3 hanno valori fissi di resistenza
rispettivamente uguali a R2=100Ω eR3=200Ω. Il valore della resistenza del resistore R1 invece
può essere variato con continuità. Sapendo che le loro f.e.m. valgono rispettivamente V1=40 V e
V2=80 V, si calcoli il valore che deve assumere R1 affinché la potenza dissipata in R2 sia
minima. (Suggerimento: guardare con attenzione l’espressione della corrente che si ottiene,
non c’è bisogno di eseguire derivate)
(Punti 6)
i2
i3
Scelto il verso di percorrenza orario deve essere
⎧
⎪
I1 = I 2 + I 3
⎪
⎪
I 2 R2 − V2
R3 + I 2 ( R2 + R3 ) = 0
⎨V1 +
R1
⎪
⎪
I R −V
I3 = 2 2 2
⎪
R1
⎩
R3V2 − R1V1
R1V1 + R2 R3 I 2 − R3V2 + I 2 R1 ( R2 + R3 ) = 0 I 2 =
R2 R3 + R1 ( R2 + R3 )
⎧
⎪
I1 = I 2 + I 3
I1 = I 2 + I 3
⎧
⎪
⎪⎪
⎨ −V1 − I1 R3 − I 2 R2 = 0 ⎨V1 + ( I 2 + I 3 ) R3 + I 2 R2 = 0
⎪−V + I R − I R = 0 ⎪
I R −V
⎩ 2 2 2 3 1
⎪
I3 = 2 2 2
R1
⎩⎪
La potenza dissipata in R2 vale
( R3V2 − R1V1 ) × R2
× R2 =
2
( R2 R3 + R1 ( R2 + R3 ) )
2
W2 = I
2
2
dall’espressione precedente si vede che W2 è minima solo quando si annulla il numeratore, cioè
V
80V
R1 = 2 R3 =
× 200 Ω = 400 Ω
V1
40V
47. Dato il circuito RC in figura, per il quale C=1 μF, determinare:
a) la differenza di potenziale ai capi del condensatore, supponendo che il circuito sia collegato
Fisica 2
Corso di Laurea in Informatica
alla batteria da un tempo molto lungo;
b) una volta disconnessa la batteria, in quanto tempo la d.d.p. ai capi del condensatore si riduce
al 10% del suo valore iniziale.
(Punti 7)
(a) Detti L ed R rispettivamente gli estremi sinistro e destro del condensatore
(b) Disconnettendo la batteria il circuito diventa
, pertanto
48. Scrivere (a) la configurazione elettronica del potassio K (Z=19) nello stato fondamentale e (b) i
valori dei numeri quantici per ciascun elettrone.
(a) 1s2 2s2 2p6 3s2 3p6 4s1
(b) n=1 l=0 ml=0 ms=±½
totale 2
n=2 l=0 ml=0 ms=±½
totale 2
n=2 l=1 ml=-1,0,1 ms=±½
totale 6
n=3 l=0 ml=0 ms=±½
totale 2
n=3 l=1 ml=-1,0,1 ms=±½
totale 6
n=3 l=0 ml=0 ms=+1/2 (o -1/2)
totale 1
Totale generale
19 elettroni
Fisica 2
Corso di Laurea in Informatica
49. Trovare (a) la lunghezza d’onda di un elettrone di energia cinetica 4 eV e (b) la lunghezza
d’onda di un fotone di energia 4 eV.
1 2 p2
da cui p = 2mK quindi ( De Broglie )
( a ) K = mv =
2
2m
h
h
6.626 × 10−34 J ⋅ s
λel = =
=
= 0.613 ×10−9 m
−
−
31
19
p
2mK
2 ⋅ 9.11× 10 kg ⋅ ( 4 ×1.602 × 10 J )
(b)
ipotesi Einstein : E = hf
λ fot
quindi
−34
8
c hc ( 6.626 × 10 J ⋅ s ) ⋅ ( 3.0 × 10 m s )
= =
=
= 0.310 ×10−9 m
f
E
4 × 1.602 × 10−19 J
50. Una bobina di area 6 cm2 con 180 avvolgimenti è connessa ad una resistenza di 3 Ω. La bobina,
immersa in un campo magnetico uniforme di 0.4 T, viene messa in rotazione manualmente
intorno al proprio asse (vedi figura) ad una frequenza di 0.6 giri/sec. Determinare:
a) il valore massimo di corrente prodotta;
(Punti 6)
b) la potenza media dissipata nella resistenza.
[Suggerimento: rammentare che θ=ωt, inoltre, per potenza media si intende quella dissipata in una
singola rotazione]
0.6 giri
Φ B = BAcos (θ ) = BAcos (ωt )
s
dΦB
d
ε = −N
= − N ⎡⎣ BAcos (ωt ) ⎤⎦ = NABω sen (ωt )
dt
dt
ε max = NABω = (180 ) ⋅ (1×10−4 m 2 ) ⋅ ( 0.4 T ) ⋅ ( 2π ⋅ 0.6 s −1 ) = 0.163
ω = 2π f = 2π
(a)
I max =
(b)
ε max
R
= 5.43 × 10−2 A
P ( t ) = R ⋅ I 2 = R ⋅ ( I max ) sen 2 (ωt )
2
2 1
−2
2
=
3
Ω
⋅
5.43
×
10
⋅ = 4.42 × 10−3 W
sen
d
A
θ
θ
(
)
(
)
(
)
∫0
2
51. Una bobina di raggio 10.0 cm e composta da 15 spire circonda un lungo solenoide composto da
1000 avvolgimenti per metro e di raggio 2.0 cm (vedi figura). La corrente nel solenoide presenta
un andamento variabile nel tempo secondo la relazione I=I0·sen(νt) con I0=5.0 A e ν=120 Hz).
Trovare:
i. l’andamento in funzione del tempo della f.e.m. indotta nella bobina da 15 spire;
ii. il valore della f.e.m. indotta nella bobina da 15 spire, quando la corrente nel
solenoide è massima.
P = R ⋅ ( I max )
2
2π
Fisica 2
Corso di Laurea in Informatica
bobina da 15 spire
a) Il flusso del campo magnetico generato dal solenoide concatenato con la bobina è
Φ B = ( μ0 nI ) Asolenoide quindi la f .e.m. indotta nella bobina è
ε = −N
dΦB
dI
2
= − N μ0 n π rsolenoide
=
dt
dt
(
(
)
)(
)
(
)
= −15 4π ⋅10−7 T ⋅ m / A 1000 m −1 π ⋅ ( 0.02 m ) 5 A ⋅120 s −1 cos (120 t ) =
2
= −14.2 cos (120 t ) mV
b) la corrente nel solenoide è massima quando l’argomento del seno è pari a multipli dispari di
π/2. Corrispondentemente la f.e.m. indotta, avendo un andamento di tipo coseno, è nulla.












