Trasformazioni termodinamiche:
Esercizi svolti
9 aprile 2013
Esercizio 1
Si consideri un sistema chiuso in cui si abbia inizialmente aria a 5◦ C, ad
una pressione p1 = 1 bar, che venga in un secondo momento compressa fino
ad una pressione p2 = 10 bar. Calcolare il lavoro, il calore e la variazione di
entropia, per unità di massa, scambiati nel caso in cui l’aumento di pressione
sia realizzato secondo le seguenti trasformazioni reversibili a calore specifico
costante:
1. isoterma (1-2),
2. adiabatica (1-3),
3. politropica di esponente n=1,7 (1-4),
3. isocora (1-5).
Disegnare le trasformazioni sul piano p-v e T-s. Si assuma per semplicità che
l’aria sia un gas ideale caratterizzato da k=1,4 e R=287 J/kg K. Ripetere poi
l’esercizio assumendo che il calore specifico vari con la temperatura secondo
le formule di Langen (usare la tabella fornita a lezione).
Soluzione
Le trasformazioni sono rappresentate qualitativamente nel piano p-v in
Fig. 1.1 e nel piano T-s in Fig. 1.2.
1
Figura 1.1: Rappresentazione della trasformazione sul piano p − v.
Figura 1.2: Rappresentazione della trasformazione sul piano T − s.
Poiché, per un gas perfetto, k = cp /cv e R = cp − cv , si ottiene:
(
R
cv = k−1
= 0, 72 kJ/kgK
cp = cv · k = 1, 01 kJ/kgK
(1.1)
Inoltre, è necessario convertire la temperatura da gradi centigradi a Kelvin: T1 = 5 + 273.15 = 278, 15 K.
Per comodità, si introduca il parametro β, detto rapporto di compressione, tale per cui: β = pp21 = 10.
2
1. Trasformazione isoterma:
Questo tipo di trasformazione è a temperatura costante, quindi definita
dall’equazione T = cost.
Nel piano p-v, ricorrendo all’equazione di stato dei gas perfetti, è quindi
rappresentabile con un’iperbole equilatera di equazione pv = RT = cost, da
cui si può subito ottenere v1 = 0, 7983m3 .
Per il primo principio della termodinamica, affinché la trasformazione avvenga senza variazioni di temperatura, il lavoro fornito al sistema per comprimere il gas, dovrà essere pari al calore ceduto dal sistema verso l’esterno
(infatti, per un sistema chiuso, ∆U = cv ∆T = 0 ⇐⇒ L = −Q).
Z v2
Z v2
v2
dv
= −RT1 ln
(1.2)
pdv = −RT1
l12 = −q12 = −
v
v1
v1
v1
dall’equazione di stato dei gas perfetti applicata al caso T = cost,
v2
p1
1
=
=
v1
p2
β
(1.3)
l12 = −q12 = RT1 lnβ = 183, 81 kJ/kg
(1.4)
e quindi:
Essendo una trasformazione a temperatura costante, l’entropia sarà pari a:
q12
∆s12 = −
= −0, 6608 kJ/kgK
(1.5)
T1
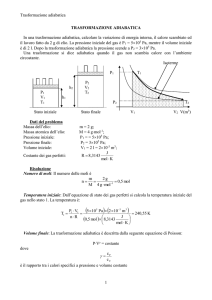
2. Trasformazione adiabatica:
Questo tipo di trasformazione è caratterizzata dall’assenza di scambi di
calore verso l’esterno (q13 = 0) ed è definita dall’equazione pv k = cost. Il
lavoro di variazione di volume associato a questa trasformazione è dato dalla
seguente:
Z v3
Z v3
k−1
− v1k−1
dv
k v3
k
=
−p
v
=
(1.6)
l13 = −
pdv = −p1 v1
1
1
k
1−k
v1
v1 v
k−1
k−1
RT1
RT1
p2 k
= −
=
1−
β k −1
k−1
p1
k−1
= 185, 64 kJ/kg
Mentre, la temperatura raggiunta dal gas in 2 è derivabile dall’equazione dell’adiabatica reversibile a calore specifico costante, in cui si utilizzi
l’equazione di stato dei gas perfetti:
T2 = T1 · β
k−1
k
3
= 537, 02 K
(1.7)
Una trasformazione adiabatica è anche isoentropica per definizione, ovvero ds = 0.
3. Trasformazione politropica:
Questo tipo di trasformazione è caratterizzata dall’equazione pv n = cost,
dove n = (c − cp )/(c − cv ). Analogamente all’adiabatica reversibile:
Z v4
Z v4
n−1
dv
− v1n−1
n
n v4
pdv = −p1 v1
=
(1.8)
l14 = −
= −p1 v1
n
1−n
v1 v
v1
n−1
n−1
RT1
RT1
p2 n
n
=
= −
1−
β
−1
n−1
p1
n−1
= 180, 28 kJ/kg
La temperatura raggiunta dal gas in 3 è, analogamente alla (1.7):
T4 = T1 · β
n−1
n
= 717, 86 K
(1.9)
Inoltre, dalla definizione di calore specifico è possibile calcolare il calore
scambiato durante la trasformazione politropica:
q14 = c(T4 − T1 ) = cv
n−k
(T4 − T1 ) = 135, 68 kJ/kg
n−1
(1.10)
La variazione di entropia è data da:
ds14 =
cdT
T
(1.11)
Integrando:
∆s14 = cv
n−k
T4
· ln = 0, 2926 kJ/kgK
n−1
T1
(1.12)
Parimenti, usando il primo principio della termodinamica:
ds14 =
dq
du + pdv
dT
dv
=
= cv
+R
T
T
T
v
(1.13)
Integrando:
∆s14 = cv ln
T4
v4
+ R · ln = 0, 2939 kJ/kgK
T1
v1
dove v4 = RT4 /p4 = 0, 2060m3 .
4. Trasformazione isocora:
4
(1.14)
Questo tipo di trasformazione è caratterizzata dall’equazione
R v v = cost,
per cui, non essendoci variazioni di volume, il termine l15 = v15 pdv è ovviamente nullo. Il gas può però essere compresso tramite un’adduzione di
calore, che dal primo principio è calcolabile come segue:
q15 = ∆u = cv (T5 − T1 )
(1.15)
È quindi prima necessario calcolare T5 , e si può fare utilizzando l’equazione di stato dei gas perfetti, applicata al caso di trasformazione isocora
(v = cost):
v
T5
T1
= cost =
=
⇒ T5 = T1 · β = 2781, 15 K
R
p2
p1
(1.16)
Da cui: q15 = 1802, 16 kJ/kg.
La variazione di entropia è data da:
ds15 =
cv dT
T
(1.17)
Integrando:
∆s15 = cv · ln
T5
= 1, 3454 kJ/kgK
T1
(1.18)
Esercizio 2
Si consideri un compressore dinamico (compressione a flusso stazionario)
che comprima aria a temperatura ambiente, da una pressione p1 = 1 bar a
una pressione p2 = 6 bar. Si determini il lavoro di compressione necessario,
nel caso in cui si realizzino le seguenti trasformazioni reversibili a calore
specifico costante:
1. adiabatica,
2. isoterma,
3. politropica con esponente n = 3,8,
4. politropica con esponente n’ = 1,23.
Si traccino le trasformazioni sul diagramma T-s. Con riferimento alla politropica di esponente n, si consideri in seconda istanza, il punto di fine compressione come un punto di fine compressione reale e si calcoli il lavoro associato alla trasformazione irreversibile. Si discutano poi le differenze con
5
il lavoro dell’adiabatica e della politropica reversibili (con esponente n). Si
assuma per semplicità che l’aria sia un gas ideale caratterizzato da k=1,4 e
R=287 J/kg K. Ripetere poi l’esercizio assumendo che il calore specifico vari
con la temperatura secondo le formule di Langen (usare la tabella fornita a
lezione).
Soluzione
Le trasformazioni sono rappresentate qualitativamente nel piano T-s in
Fig. 2.1.
Figura 2.1: Rappresentazione della trasformazione sul piano T − s.
Essendo aria, sappiamo che il gas è caratterizzato da R = 287 J/kgK.
Consideriamo la prima trasformazione: essendo un’adiabatica reversibile, essa è rappresentata dall’equazione:
pv k = cost
(2.1)
dove k = 1, 4 nel caso in cui il gas sia aria. Poiché, per un gas perfetto,
k = cp /cv e R = cp − cv è facile determinare i valori dei calori specifici:
(
R
= 0, 72 kJ/kgK
cv = k−1
(2.2)
cp = cv · k = 1, 01 kJ/kgK
6
Il lavoro associato alla compressione adiabatica reversibile sarà dato da,
(sistema aperto):
Z p2
vdp
(2.3)
l12 =
p1
k−1
k
k
=
RT1 β
− 1 = 193, 4 kJ/kg
k−1
poiché T1 = 15 + 273, 15 = 288, 15 K e β = pp21 = 6.
La temperatura del gas nel punto 2 sarà ricavabile dalla relazione (2.1),
da cui, utilizzando l’equazione di stato dei gas perfetti, si ottiene:
T2 = T1 · β
k−1
k
= 480 K
(2.4)
Consideriamo ora la trasformazione isoterma da 1 a 1’. Questa trasformazione può essere rappresentata sul piano T-s da una politropica con
n = 1. In generale, è una trasformazione caratterizzata da dT = 0 e quindi
T = cost. Il lavoro di variazione di volume connesso a tale trasformazione
risulta quindi essere:
Z p 10
l110 =
vdp =
(2.5)
p1
Z p10
dp
=
= RT1
p
p1
= RT1 lnβ = −q110 = 148, 1 kJ/kg
Per quanto riguarda la trasformazione politropica con esponente n =
3,8, essendo n > k, si vede dalla Fig. 2.1 che la trasformazione 12’ è rappresentabile con una curva più ad entropia crescente (più inclinata) rispetto
all’adiabatica reversibile. Viceversa sarà per la politropica con n’ = 1,23 <
k, rappresentata dalla curva 12”.
Ricordiamo che la generica trasformazione politropica è una trasformazione a calore specifico costante, per cui vale:
dq
= cost
dT
caratterizzata da un’esponente n, tale per cui:
c=
n=
c − cp
c − cv
7
(2.6)
(2.7)
e dunque:
c=
c − cp
m−k
= cv
c − cv
m−1
(2.8)
Per cui si ottiene: c = 0, 62 per la trasformazione 12’ (n=3,8) e c0 = −0, 53
per la 12” (n’=1,23).
Il lavoro associato alla trasformazione 12’ sarà:
Z p 20
l120 =
vdp =
(2.9)
p1
n−1
n
=
RT1 β n − 1 = 307, 8 kJ/kg
n−1
Allo stesso modo, il lavoro associato alla trasformazione 12’ sarà:
Z p200
l1200 =
vdp =
(2.10)
p1
n0 −1
n0
0
n
=
RT1 β
− 1 = 176 kJ/kg
n0 − 1
Le temperature del gas nei punti 2’ e 2” saranno ricavabili, per analogia,
dalla relazione (2.1), laddove all’esponente k si sostituiscano, rispettivamente,
gli esponenti n e n’:
n−1
(2.11)
T20 = T1 · β n = 1078 K
T200 = T1 · β
n0 −1
n0
= 402, 7 K
(2.12)
Applicando il primo principio della termodinamica per sistemi aperti1 ,
si può osservare come il lavoro netto l120 sia calcolabile anche come il salto
entalpico più una certa quantità di calore assorbito, per la trasformazione
12’:
l120 = ∆h − q120 = cp (T20 − T1 ) − c(T20 − T1 ) = 308, 1 kJ/kg
(2.13)
che coincide con quanto ottenuto nella (2.9).
Mentre per la trasformazione 12”, il lavoro netto l1200 è pari al salto
entalpico più una certa quantità di calore ceduto:
l1200 = ∆h − q1200 = cp (T200 − T1 ) − c0 (T200 − T1 ) = 176, 5 kJ/kg
che coincide con quanto ottenuto nella (2.10).
1
δq = dh + vdp ⇒ q12 = (h2 − h1 ) +
R p2
p1
vdp = (h2 − h1 ) − l12
8
(2.14)
Osservazioni
Si osservi che la trasformazione meno dispendiosa risulta essere l’isoterma, a cui è associato un minore lavoro richiesto per la compressione. Tale
trasformazione è tuttavia tecnicamente irrealizzabile, perché richiederebbe
grandi superfici di scambio per poter mantenere costante la temperatura,
nonostante i tempi ridotti. In Fig. 2.1, il lavoro di compressione isoterma (si
ricordi che per una isoterma l = −q) è rappresentabile con l’area A1’1C.
Il lavoro associato all’adiabatica reversibile (corrispondente a una isoentropica, e viceversa2 ), per la definizione di calore specifico a pressione costante3 , può essere visto come il calore scambiato lungo una qualsiasi isobara per
portare il fluido da T1 a T2 : area A1’2C. Analogamente, il lavoro associato alla trasformazione politropica reversibile (consideriamo il caso con esponente
n>k), dato dalla (2.9), sarà rappresentato dall’area A1’2’1C.
La stessa figura può essere utile per valutare le differenze tra la politropica
reversibile e la trasformazione adiabatica reale (irreversibile). Entrambe le
trasformazioni sono rappresentabili con la curva 12’. Il lavoro dell’adiabatica
reale sarà però dato dall’area A1’2’D e sarà calcolabile come:
T20
cp
=
(2.15)
l120 ,IRR = cp (T20 − T1 ) = RT1 1 −
R
T1
n−1
cp
n
=
−1 =
RT1 β
cp − cv
n−1
k
n
=
RT1 β
− 1 = 797, 9 kJ/K
k−1
Ottenibile anche considerando c = 0 (adiabatica) in Eq. (2.13).
Si può osservare che: A1’2’D = A1’2C + C12’D + 122’, dove: A1’2C
rappresenta, come già detto, il lavoro associato alla politropica reversibile;
C12’D è il lavoro passivo, cioè l’energia dissipata per effetto dell’attrito e può
essere visto come calore da introdurre nella trasformazione reversibile per
ottenere l’effetto del calore generato dalla dissipazione di energia meccanica
per effetto dell’attrito presente nella trasformazione irreversibile:
lp = l120 − l120 ,IRR = 490, 1 kJ/K
(2.16)
Infine, l’area 122’ (area in giallo in Fig. 2.1) rappresenta il cosiddetto
lavoro di controrecupero, ovvero quel lavoro in più che si rende necessario
per contrastare la dilatazione provocata dall’attrito e che fa sì che l120 ,IRR −
2
3
Per le trasformazioni reversibili: T ds = dq ⇒ dq = 0 ⇐⇒ ds = 0
∆h
cp = ∆T
, dove nell’isobara ∆h = q mentre nell’adiabatica ∆h = l
9
l120 > lp :
lCR = l12 − l120 = 115 kJ/K
(2.17)
Esercizio 3
Si consideri un sistema cilindro-pistone che non scambia massa con l’esterno e realizza un ciclo termodinamico costituito dalla successione di tre
trasformazioni reversibili:
1. Compressione isoterma tra gli stati 1 e 2 (T1 =0◦ C, p1 =1 bar, p2 =60
bar),
2. Adduzione di calore isobara tra gli stati 2 e 3,
3. Espansione adiabatica tra gli stati 3 e 1.
Il fluido che subisce le trasformazioni è un gas ideale di massa unitaria (m=1
kg), monoatomico, con massa molare 40 kg/kmol. Disegnare le trasformazioni sul piano p-v e T-s e determinare il rendimento termodinamico del
ciclo.
Soluzione
Le trasformazioni sono rappresentate qualitativamente nei piani p-v e T-s
in Figg. 3.1 e 3.2.
Figura 3.1: Rappresentazione del ciclo termodinamico sul piano p − v.
10
Figura 3.2: Rappresentazione del ciclo termodinamico sul piano T − s.
Si noti che il sistema, non scambiando massa con l’esterno, è un sistema
chiuso.
Il rendimento di un ciclo termodinamico è dato dal rapporto tra il lavoro
utile Lu e il calore assorbito Q1 (ciò che si è ottenuto a fronte di ciò che si è
speso):
Lu
η=
(3.1)
Q1
Poiché il fluido subisce delle trasformazioni che lo riportano alle condizioni
iniziali, si ha una variazione netta di energia interna nulla, per cui per il primo
principio dovrà essere:
Lu = Q1 − |Q2 | ⇒ η = 1 −
|Q2 |
Q1
(3.2)
dove Q2 è il calore ceduto, negativo per convenzione, da cui la necessità del
valore assoluto.
Si noti che per un gas monoatomico con massa molare 40 kg/kmol:
R = 8314/40 = 207, 8 J/kg · K
(3.3)
Per la trasformazione di compressione isoterma, si ha che T = cost
(dT = 0) per cui T2 = T1 = 273, 15 K. Il lavoro di variazione di volume è
pari a:
Z
V2
L12 = −Q12 = −
pdV
V1
11
(3.4)
Dall’equazione di stato dei gas perfetti, applicata ad una isoterma:
p1 V1 = p2 V2 ⇒
V2
p1
=
V1
p2
(3.5)
Quindi, la (3.4) diventa:
Z
V2
L12 = −Q12 = −mRT1
V1
= −mRT1 ln
dV
V
(3.6)
p1
V2
= −mRT1 ln
V1
p2
= 232, 45 kJ
Per la trasformazione isobara di adduzione di calore si ha p = cost
(dp = 0) per cui p3 = p2 .
Per il lavoro e il calore scambiati valgono:
Z V3
L23 = −
pdV = p2 cdot(V2 − V3 )
(3.7)
V2
Q23 = mcp · ∆T = mcp (T3 − T2 )
dove, essendo il gas monoatomico,
(
cv = 25 R = 519, 6 J/kgK
cp = 32 R = 727, 5 J/kgK
(3.8)
(3.9)
Risulta necessario calcolare V2 , V3 e T3 .
T3 può essere ottenuta considerando la terza trasformazione: essendo
un’espansione adiabatica reversibile, questa è caratterizzata da:
p3 V3k = cost = p1 V1k
(3.10)
dove k = cp /cv = 1, 4, usando l’Eq. (3.9).
Usando l’equazione di stato dei gas perfetti, nella (3.10):
p3 = mR
1−k
1−k
T3
T1
, p1 = mR ⇒ T1 p1 k = T3 p3 k
V3
V1
(3.11)
1−k
e quindi T3 = T1 ( pp12 ) k = 880 K = 606, 85◦ C.
Utilizzando di nuovo l’equazione di stato dei gas perfetti:
V3 = mR
T3
= 3, 05 · 10−2 m3
p3
12
(3.12)
V2 = mR
T2
= 9, 46 · 10−3 m3
p2
(3.13)
A questo punto, sostituendo in Eqq. (3.7) e (3.8), si ha:
Q23 = 441, 5 kJ
L23 = −126 kJ
Per l’espansione adiabatica reversibile, si ha che il calore scambiato
è nullo, Q31 = 0, mentre il lavoro può essere calcolato come:
Z V1
Z V1
dV
p3 V3k k
pdV = −
L31 = −
(3.14)
V
V3
V3
V11−k − V31−k
1−k
p1 V1 − p3 V3
=
k−1
= −p3 V3k
dall’equazione di stato dei gas perfetti:
V1 = mR
T1
= 0, 568 m3
p1
(3.15)
Sostituendo in Eq. (3.14), si ottiene quindi L31 = −315, 6 kJ.
Il lavoro utile del ciclo risulta allora essere:
Lu = L12 + L23 + L31 = −209, 15 kJ
(3.16)
negativo perché fatto dal sistema sull’ambiente esterno (energia uscente dal
sistema).
Il calore totale scambiato risulta invece:
Qtot = Q12 + Q23 = 209, 05 kJ
(3.17)
E si vede come, a meno di errori di approssimazione, Lu = −Qtot .
Finalmente, dall’Eq. (3.2):
η =1−
|Q12 |
= 0, 473
Q23
13
(3.18)
Esercizio 4
Si consideri di avere 1 kg di azoto a pressione atmosferica, in un ambiente di 1 m3 che non può scambiare massa con l’esterno. Il gas viene poi
sottoposto a un ciclo termodinamico così composto:
1. compressione con rapporto di compressione β = 3, 5 (trasformazione
politropica con n=1,3)
2. trasformazione isocora fino alla pressione iniziale
3. trasformazione isobara fino alle condizioni iniziali
Rappresentare il ciclo sul piano p-v e determinare il lavoro netto del ciclo e
il calore totale scambiato. Ripetere poi l’esercizio assumendo che la prima
trasformazione dia un’adiabatica reversibile e che il calore specifico vari con la
temperatura secondo le formule di Langen (usare la tabella fornita a lezione).
Soluzione
Le trasformazioni sono rappresentate qualitativamente nel piano p-v in
Fig. 4.1.
Figura 4.1: Rappresentazione del ciclo termodinamico sul piano p − v.
Si inizi con il considerare che l’azoto è un gas biatomico con peso molecolare M = 28, 01 kg/kmol da cui si può ricavare R = 8314/28, 01 =
14
296, 8 J/kgK e k = 7/5 = 1, 4. Poiché, per un gas perfetto, k = cp /cv e
R = cp − cv , si ottiene:
(
R
cv = k−1
= 0, 742 kJ/kgK
(4.1)
cp = cv · k = 1, 04 kJ/kgK
Inoltre, è possibile calcolare la temperatura iniziale dall’equazione di stato
dei gas perfetti (pressione atmosferica: p1 = 1 bar):
T1 =
p1 V1
= 337 K
mR
(4.2)
Poiché β = 3, 5, p2 = 3, 5 bar.
1. Trasformazione politropica:
La temperatura raggiunta dal gas dopo la compressione sarà calcolabile
dall’equazione della politropica:
T2 = T1 β
n−1
n
= 450 K
(4.3)
mentre per il volume:
n1
1
= 0, 382 m3
V2 = V1
β
Il lavoro della compressione politropica sarà pari a:
Z V2
Z V2
dV
n
L12 = −
pdV = −p1 V1
n
V1
V1 V
n−1
RT1
=
β n −1
n−1
= 111, 76 kJ
(4.4)
(4.5)
Inoltre, dalla definizione di calore specifico, si può calcolare il calore
scambiato:
Q12 = mc(T2 − T1 ) = mcv
n−k
(T2 − T1 ) = −27, 95 kJ
n−1
(4.6)
2. Trasformazione isocora:
Questo tipo di trasformazione è caratterizzata dall’equazione V = cost
(V3 = V2 = 0, 382 m3 ), per cui, non essendoci variazioni di volume, il termine
RV
L23 = V23 pdV è ovviamente nullo.
15
Il gas può però essere espanso tramite una sottrazione di calore, che dal
primo principio è calcolabile come segue:
Q23 = mcv (T3 − T2 )
(4.7)
È quindi prima necessario calcolare T3 , che dall’equazione di stato dei gas
perfetti (si consideri che p3 = p1 = 1 bar), è data da:
T3 =
p3 V3
= 128 K
mR
(4.8)
da cui: Q23 = −238, 9 kJ.
3. Trasformazione isobara:
Questo tipo di trasformazione è caratterizzata dall’equazione p = cost.
Il lavoro di espansione libera sarà pari a:
Z V1
L31 = −
pdV = p(V3 − V1 ) = −61, 8 kJ
(4.9)
V3
Mentre per il calore avremo:
Q31 = mcp · ∆T = mcp (T1 − T3 ) = 217, 36 kJ
(4.10)
Il lavoro netto del ciclo sarà quindi dato dalla somma algebrica dei lavori
associati alle diverse trasformazioni (si ricordi che la trasformazione isocora
è a lavoro di variazione di volume nullo):
Lu = L12 + L31 = 49, 76 kJ
(4.11)
Il calore totale scambiato sarà analogamente dato dalla somma algebrica
dei calori scambiati durante le diverse trasformazioni:
Qtot = Q12 + Q23 + Q31 = −49, 49 kJ
(4.12)
E si vede come, a meno di errori di approssimazione, Lu = Qtot .
Risolviamo lo stesso esercizio considerando che la compressione avvenga
adiabaticamente e che cp e cv siano variabili con la temperatura secondo le
equazioni di Langen: cp = a + bT e cv = a0 + bT .
Per l’azoto, a = 0, 986 kJ/kgK, a0 = 0, 69 kJ/kgK, b = 0, 000150 kJ/kgK 2 .
Dalla formula di Mayer: R = cp −cv = a−a0 = 0, 296 kJ/kgK. Si noti che
è lo stesso valore ottenuto in precedenza, infatti la costante universale dei gas
dipende solo dalle proprietà chimiche del gas e non da quelle termodinamiche.
16
La temperatura iniziale rimane definita dall’equazione di stato dei gas
perfetti (pressione atmosferica: p1 = 1 bar):
T1 =
p1 V1
= 337 K
mR
(4.13)
Poiché β = 3, 5, p2 = 3, 5 bar.
1. Trasformazione adiabatica:
Per calcolare la temperatura raggiunta dal gas dopo la compressione attraverso l’equazione dell’adiabatica reversibile, occorre utilizzare la seguente:
T2 = T1 β
k−1
k
(4.14)
che però non è risolvibile analiticamente poiché, tramite Langen, k dipende
da T2 . In particolare, senza commettere un grande errore, il k può essere
determinato come funzione della temperatura media (T1 + T2 )/2.
k̄ =
a + b(T1 + T2 )/2
cp
=
cv
a + b0 (T1 + T2 )/2
(4.15)
Poiché, come detto, T2 è l’incognita, il problema va risolto iterativamente. Si
identifica un valore di primo tentativo, per T2 che può essere scelto applicando
la relazione dell’adiabatica dove si utilizzi k(T = T1 ).
k̄ (1) =
(1)
T2
a + bT1
cp
=
= 1, 3981
cv
a + b0 T1
= T1 β
k̄(1) −1
k̄(1)
(4.16)
= 481, 4400 K
(4.17)
(1)
k̄
(2)
=
(2)
T2
a + b(T2 + T1 )/2
(1)
a + b0 (T2 + T1 )/2
= T1 β
k̄(2) −1
k̄(2)
= 1, 3922
(4.18)
= 479, 6148 K
(4.19)
(1)
k̄
(3)
=
(3)
T2
a + b(T2 + T1 )/2
(1)
a + b0 (T2 + T1 )/2
= T1 β
k̄(3) −1
k̄(3)
= 1, 3921
(4.20)
= 479, 5908 K
(4.21)
(3)
(3)
Già ci si può fermare, poiché l’errore commesso tra T2 e T2 è meno
dell’1%. Per completezza, lo verifichiamo con un’ulteriore iterazione:
(4)
k̄ (4) =
a + b(T2 + T1 )/2
(4)
a + b0 (T2 + T1 )/2
17
= 1, 3921
(4.22)
(4)
T2
= T1 β
k̄(4) −1
k̄(4)
= 479, 5911 K
(4.23)
da cui si vede che la temperatura non cambia significativamente.
Dall’equazione dei gas perfetti è poi possibile calcolare il volume alla fine
della compressione:
RT2
V2 =
= 0, 406 m3
(4.24)
p2
Il lavoro della compressione adiabatica sarà pari a:
Z V2
Z V2
dV
k̄
pdV = −p1 V1
L12 = −
k̄
V1
V1 V
k̄−1
RT1
β k̄ − 1
=
k̄ − 1
= 107, 64 kJ
(4.25)
2. Trasformazione isocora:
Questo tipo di trasformazione è caratterizzata dall’equazione V = cost
(V3 = V2 = 0, 406 m3 ), per cui, non essendoci variazioni di volume, il termine
RV
L23 = V23 pdV è ovviamente nullo.
Il calore dal primo principio è funzione di cv che calcoleremo come valore
medio tra T2 e T3 :
Q23 = mcv (T3 − T2 ) = m(a0 + b(T3 + T2 )/2)(T3 − T2 )
(4.26)
È quindi prima necessario calcolare T3 , che dall’equazione di stato dei gas
perfetti (si consideri che p3 = p1 = 1 bar), è data da:
T3 =
p3 V3
= 137, 03 K
mR
(4.27)
da cui: Q23 = −253, 2 kJ.
3. Trasformazione isobara:
Questo tipo di trasformazione è caratterizzata dall’equazione p = cost.
Il lavoro di espansione libera sarà pari a:
Z V1
L31 = −
pdV = p(V3 − V1 ) = −59, 40 kJ
(4.28)
V3
18
Mentre per il calore avremo:
Q31 = mcp · ∆T = m(a + b(T3 + T1 )/2)(T1 − T3 ) = 204, 71 kJ
(4.29)
Il lavoro netto del ciclo sarà quindi dato dalla somma algebrica dei lavori
associati alle diverse trasformazioni (si ricordi che la trasformazione isocora
è a lavoro di variazione di volume nullo):
Lu = L12 + L31 = 48, 24 kJ
(4.30)
Il calore totale scambiato sarà analogamente dato dalla somma algebrica
dei calori scambiati durante le diverse trasformazioni:
Qtot = Q12 + Q23 + Q31 = −48, 49 kJ
(4.31)
E si vede come, a meno di errori di approssimazione, Lu = Qtot .
Esercizio 5
Si consideri di far evolvere in una turbina dinamica una portata di vapore
acqueo di 80 kg/s, inizialmente alla temperatura di 550◦ C. Sapendo che
il salto di pressione è ∆p = 179 bar, valutare la differenza percentuale di
potenza meccanica estraibile nel caso in cui sia pf = 1 bar e pf = 0, 01 bar.
Si consideri che la trasformazione di espansione sia un’adiabatica reversibile.
Soluzione
La potenza meccanica estraibile da una turbina è pari a:
Pmecc = ṁ · lt
(5.1)
dove, essendo la turbina un sistema aperto e la trasformazione un’adiabatica
(q = 0), dal primo principio:
lt = hi − hf
(5.2)
Caso 1: pf = 1bar
L’entalpia nel punto 3 può essere determinata dalle tabelle del vapore
surriscaldato, in funzione di Ti = 550◦ C e pi = ∆p + pf = 180 bar:
hi = 3416, 1 kJ/kg
19
Per determinare l’entalpia del punto finale, essendo la trasformazione
isoentropica, si può sfruttare l’informazione sull’entropia si = sf , dove, dalle
tabelle del vapore surriscaldato, si = 6, 4069 kJ/kgK.
A questo punto, è possibile calcolare il titolo di fine espansione, da cui
poi sarà possibile ottenere il valore di entalpia nel punto finale. Il titolo può
essere calcolato con la regola della leva, dove il pedice cli si riferisce alla curva
limite inferiore, cioè alle condizioni di liquido saturo , mentre cls si riferisce
alla curva limite superiore, cioè alle condizioni di vapor saturo:
x=
6, 4069 kJ/kgK − 1, 3027 kJ/kgK
sf − scli
=
= 0, 84
scls − scli
7, 3598 kJ/kgK − 1, 3027 kJ/kgK
(5.3)
Per lo stesso principio:
hf − hcli
⇒
(5.4)
hcls − hcli
= x(hcls − hcli ) + hcli =
= 0.84 · (2675, 4 kJ/kg − 417, 51 kJ/kg) + 417, 51 kJ/kg
= 2314.14 kJ/kg
x =
hf
Da cui:
Pmecc,1 = ṁ · lt = ṁ · (hi − hf ) = 88, 16 M W
(5.5)
Caso 2: pf = 0, 01bar
L’entalpia nel punto 3 può essere agevolmente determinata dalle tabelle del vapore surriscaldato, in funzione di Ti = 550◦ C e pi = ∆p + pf =
179, 01 bar. Questa volta si rende necessaria un’interpolazione, da cui si
ottiene:
hi = 3417, 2 kJ/kg
Per determinare l’entalpia del punto finale, essendo la trasformazione
isoentropica, si può sfruttare l’informazione sull’entropia si = sf , dove, dalle
tabelle del vapore surriscaldato, interpolando, si = 6, 4100 kJ/kgK. (Si può
notare come i valori dell’entalpia e dell’entropia siano variati irrisoriamente,
per il vapore surriscaldato).
A questo punto, è possibile calcolare il titolo di fine espansione, da cui
poi sarà possibile ottenere il valore di entalpia nel punto finale. Il titolo può
essere calcolato con la regola della leva:
x=
6, 4100 kJ/kgK − 0, 1060 kJ/kgK
sf − scli
=
= 0, 71
scls − scli
8, 9767 kJ/kgK − 0, 1060 kJ/kgK
20
(5.6)
Per lo stesso principio:
hf − hcli
⇒
hcls − hcli
= x(hcls − hcli ) + hcli =
= 0, 71 · (2514, 4 kJ/kg − 29, 34 kJ/kg) + 29, 34 kJ/kg
= 1795, 32 kJ/kg
x =
hf
(5.7)
(Si può adesso notare come i valori dell’entalpia e dell’entropia siano
variati significativamente per il vapore saturo).
Da cui:
Pmecc,2 = ṁ · lt = ṁ · (hi − hf ) = 129, 75 M W
(5.8)
La variazione percentuale di potenza meccanica estraibile è del 47%,
infatti:
∆Pmecc = (Pmecc,1 − Pmecc,2 )/Pmecc,1 = 0, 47
(5.9)
Questo può essere spiegato considerando che il lavoro trasferito dal fluido
alla turbina (sistema aperto) è dato da:
Z pf
vdp
(5.10)
lt = −
pi
e, a parità di ∆p, l’equazione di Clapeyron4 ci dice che il volume specifico
aumenta di molto al diminuire della pressione di saturazione, poiché la derivata della temperatura rispetto alla pressione, in saturazione, assume valori
cospicui.
4 dTsat
dpsat
= Tsat ∆v
r , con r calore latente
21