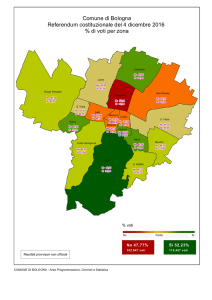
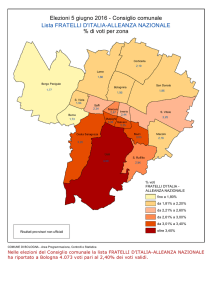
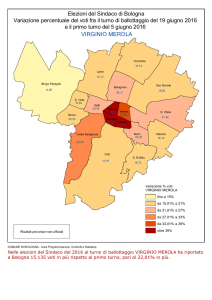
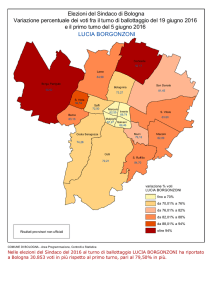
Le formule elettorali
Le formule elettorali
• La domanda: come tradurre i voti in seggi?
1. Maggioritaria
2. Proporzionale
3. Sistemi misti
Formule maggioritarie
•
•
Le due formule principali:
• Maggioranza assoluta (ossia il 50% dei voti +1)
• Maggioranza relativa o plurality system
I quattro tipi:
• Sistema maggioritario ad un turno in collegi uninominali
(first past the post)
• Sistema maggioritario ad un turno in collegi plurinominali:
il caso del voto singolo non trasferibile (Giappone 19471993)
• Sistema maggioritario a doppio turno in collegi
uninominali
• Voto alternativo in collegi uninominali (Australia; elezioni
presidenziali in Irlanda)
Il sistema a doppio turno
•
•
•
Sistema maggioritario a doppio turno in collegi
uninominali: vince chi ha la maggioranza assoluta al 1°
turno, altrimenti 2° turno: majority (se si ha ballottaggio
solo tra due candidati) oppure plurality (se ammessi al
ballottaggio più di due candidati)
Criterio per l’ammissione dei candidati al 2° turno:
• Doppio turno aperto (ha comunque delle
conseguenze!)
• Doppio turno chiuso (2° turno con ballottaggio o
soglia di ammissione : es. Francia > 12,5%)
Il sistema a doppio turno in Italia per eleggere i sindaci (al
di sopra dei 15 mila abitanti) e i presidenti provinciali
Procedimento elettorale con voto alternativo (Australia)
Candidati
Adams
Brown
Grey
Jones
White
Tot.
Prime preferenze
15.000
20.000
7.000
10.000
8.000
60.000
Redistr. schede Grey
1.000
-
4.000
2.000
Nuovo totale (1)
16.000
20.000
14.000
10.000
Redistr. schede White
1.500
3.000
5.500
Nuovo totale (2)
17.500 23.000
19.500
Redistr. schede Adams
6.000
11.500
Situazione finale
29.000
31.000
Formule proporzionali - I
• Formule volte a consentire che tutti gli
orientamenti politici siano rappresentati in
“proporzione” alle loro forze: richiesti per
definizione dei collegi plurinominali
• La maggior parte dei sistemi proporzionali
adottano il voto di lista
• Come effettuare il riparto dei voti?
• Il metodo della quota/quoziente
• Il metodo dei divisori
Formule proporzionali - II
• Il metodo della quota: la quota è il numero dei voti
che bisogna raggiungere per ottenere un seggio
• Più in dettaglio: la formula di Hare (o dei resti più
alti)
• Se in un collegio ci sono V elettori/voti espressi
e N seggi, la quota di Hare è la parte intera del
rapporto tra V e N, vale a dire: q(Hare) = (V/N)
• Un partito che riceve M voti otterrà quindi
[M/q(Hare)] seggi
• I seggi non distribuiti in questo modo sono
assegnati ai partiti che hanno i resti più alti
Ripartizione seggi secondo la formula Hare
(quoziente e più alti resti) (Germania, Italia Camera pre94)
Partiti
N.seggi = 8 Voti espressi: 423.00
Quoziente: 423.000/8 =52.875
Voti Quoziente Seggi
Resti
pieni
Seggi
A
171.000
3,23
3
12.365
3
B
132.000
2,49
2
26.250
2
C
84.000
1,58
1
31.125
2
D
36.000
0,68
0
36.000
1
Formule proporzionali - III
•
Il metodo dei divisori: si parte dall’idea che un partito è
peggio rappresentato di un altro se è più alto il rapporto
tra i voti ricevuti e i seggi ottenuti (nell’es. precedente:
per il partito A 57.000 voti per ogni seggio; partito D
36.000 voti per ogni seggio) ⇒ cercare di mantenere il
più possibile uguale tra loro i rapporti tra i voti e i
seggi dei vari partiti
Formule proporzionali - IV
•
•
Metodo d'Hondt: si dividono i totali di voti delle liste
per 1,2,3,4,5... fino al numero di seggi da assegnare nel
collegio, e si assegnano i seggi in base ai risultati in
ordine decrescente fino ad esaurimento dei seggi da
assegnare
Con la formula Sainte-Lagüe cambiano i divisori che
sono 1,4; 3; 5 e 7, ma non il metodo
Ripartizione seggi secondo la formula
d’Hondt: passo per passo
Partiti
tot. voti
primo seggio
risultato
secondo seggio
rilsultato
terzo seggio
risultato
quarto seggio
risultato
quinto seggio
risultato
sesto seggio
risultato
settimo seggio
risultato
ottavo seggio
risultato
Tot. Seggi
A
171.000
(171000/1)=171000
seggio ad A
(171.000/2)=85500
(171.000/2)=85500
seggio ad A
(171000/3)=57000
(171000/3)=57000
(171000/3)=57000
seggio ad A
(171000/4)=42750
(171000/4)=42750
seggio ad A
4
B
132.000
(132000/1)=132000
C
84.000
(84000/1)=840000
D
36.000
(36000/1)=36000
(132000/1)=132000
seggio a B
(132000/2)=66000
(84000/1)=840000
(36000/1)=36000
(84000/1)=840000
(36000/1)=36000
(132000/2)=66000
(84000/1)=840000
seggio a C
(84000/2)=42000
(36000/1)=36000
(36000/1)=36000
(84000/2)=42000
(36000/1)=36000
(132000/2)=66000
seggio a B
(132000/3)=44000
(132000/3)=44000
seggio a B
(132000/4)=33000
(84000/2)=42000
(36000/1)=36000
(84000/2)=42000
(36000/1)=36000
3
1
0
Ripartizione seggi secondo la formula
d’Hondt (Austria, Belgio, Finlandia, Italia pre94 Senato, Spagna)
N.seggi = 8
Partiti
Divisori
Voti
1
2
3
4
Seggi
A
171.000
171.000
(1)
85.500
(3)
57.000
(6)
42.750
(8)
4
B
132.000
132.000
(2)
66.000
(5)
44.000
(7)
33.000
3
C
84.000
84.000
(4)
42.000
28.000
21.000
1
D
36.000
36.000
18.000
12.000
9.000
0
Ripartizione seggi secondo la formula SainteLagüe modificata (Danimarca, Norvegia, Svezia)
N.seggi = 8
Partiti
Divisori
Voti
1,4
3
5
7
Seggi
A
171.000
122.142
(1)
57.000
(4)
34.200
(6)
24.428
3
B
132.000
94.285
(2)
44.000
(5)
26.400
(8)
18.857
3
C
84.000
60.000
(3)
28.000
(7)
16.800
12.000
2
D
36.000
25.714
12.000
7.200
5.143
0
Formule proporzionali - IV
• Il risultato: l’adozione di diverse formule
proporzionali, a partire da una stessa distribuzione
dei voti, può determinare allocazioni di seggi
abbastanza differenti: ad es., la formula d’Hondt
determina un leggero vantaggio a favore dei grandi
partiti, a discapito di quelli più piccoli
• Formula proporzionale e voto non di lista: il caso
del voto singolo trasferibile (Irlanda, Malta,
Australia – Senato federale)
Formule miste
•
•
La premessa: si combinano elementi derivanti da sistemi
elettorali ispirati a principi diversi
Esempi:
• Germania: combina collegi uninominali – sistema
maggioritario (50%) - assieme a collegi plurinominali –
sistema proporzionale (50%). Si attribuisce agli elettori
voti distinti per le due componenti
• Italia (dalle elezioni del 1994 fino a quelle del 2001):
75% dei seggi assegnati in collegi uninominali con il
sistema maggioritario ad un turno; 25% con sistema
proporzionale. Alla Camera l’elettore dispone di due
voti separati, al Senato il voto è unico
Soglie di rappresentanza
•
Soglie esplicite:
1.
2.
•
una percentuale minima di voti a livello nazionale
(Italia) o circoscrizionale (Spagna)
l’accesso al riparto dei resti nella circoscrizione più
ampia sulla base di criteri restrittivi (Germania)
Soglie implicite:
1.
2.
3.
ampiezza dell’organo da eleggere (più ampio, minore
soglia)
grandezza del collegio (alla crescita del numero di
eletti in un collegio, diminuisce la soglia)
a che livello avviene la ripartizione dei seggi
Formule miste: il caso italiano (I)
– come era: dal 1994 al 2001
•
Camera (aspetti principali):
-
-
-
suddivisione del territorio nazionale in 26 circoscrizioni di
dimensione regionale o infraregionale;
attribuzione, in ogni circoscrizione, del 75% dei seggi con la
formula maggioritaria nell'ambito di altrettanti collegi uninominali;
ripartizione in ambito nazionale dei restanti seggi con la formula
proporzionale dei quozienti interi e di più alti resti. E' prevista una
soglia di sbarramento del 4%;
attribuzione a ciascun elettore di due voti su schede distinte: uno
per l'elezione del candidato nel collegio uninominale, uno per la
scelta di una delle liste circoscrizionali concorrenti al riparto dei
seggi in ragione proporzionale;
scorporo parziale dai voti conseguiti dalle liste dei voti necessari
per eleggere, nei collegi uninominali, i candidati collegati a
ciascuna lista.
Formule miste: il caso italiano (II)
- come era: dal 1994 al 2001
•
Senato (aspetti principali):
•
•
•
•
attribuzione in ogni regione di tre quarti dei seggi con sistema
maggioritario a turno unico nell'ambito di altrettanti collegi
uninominali; fanno eccezione la regione Valle d'Aosta, che è
costituita in un unico collegio uninominale e la regione Molise, il
cui territorio è ripartito in due collegi uninominali;
ripartizione dei restanti seggi spettanti alla Regione con sistema
proporzionale (secondo il metodo d'Hondt) nell'ambito della
circoscrizione regionale tra gruppi di candidati concorrenti nei
collegi uninominali;
attribuzione a ciascun elettore di un solo voto, da esprimere a
favore di uno dei candidati presentati nel collegio uninominale;
sottrazione totale dalla cifra elettorale di ciascun gruppo dei voti
conseguiti dai candidati eletti nei collegi uninominali (c.d.
“scorporo totale”).
Il caso italiano: come è dal 2006 (I)
•
•
•
•
•
•
Camera (aspetti principali):
Sistema proporzionale: ripartizione seggi secondo la formula
Hare (quoziente e più alti resti) in un unico collegio nazionale
Voto di lista bloccato
I partiti collegati in coalizioni presentano un unico programma
elettorale in cui viene indicato il nome della persona come
capo della coalizione
Soglie di sbarramento: 4% per un partito che corre da solo;
2% per un partito legato a una colazione che ha ottenuto
complessivamente almeno il 10%
Premio di maggioranza: alla coalizione vincente sono
assegnati, nel caso non li ottenga dalle urne, 340 seggi (il 54%
dei 630 seggi tot.). Poiché la maggioranza è di 316 seggi, il
futuro governo ha un margine di almeno 24 deputati
Il caso italiano: come è dal 2006 (II)
•
•
•
•
•
Senato (aspetti principali):
Sistema proporzionale: ripartizione seggi secondo la formula
Hare (quoziente e più alti resti) su base regionale
Voto di lista bloccato
Soglie di sbarramento (calcolate regione per regione): 8% per
un partito che corre da solo; 3% per un partito legato a una
colazione che ha ottenuto complessivamente almeno il 20%
Premio di maggioranza: alla coalizione vincente nella singola
regione sono assegnati, nel caso non li ottenga dalle urne, il
55% dei seggi assegnati alla Regione (con arrotondamento
all’unità superiore). Risultato: potranno esserci maggioranza
diverse regione per regione
Testi di riferimento per la lezione
• Maurizio Cotta - Donatella Della Porta - Leonardo
Morlino, Fondamenti di scienza politica, Il Mulino,
Bologna, 2001, cap.8
• Gianfranco Pasquino, Nuovo corso di scienza
politica, Il Mulino, Bologna, 1997, cap.5