SCOMPOSIZIONE IN FATTORI PRIMI:

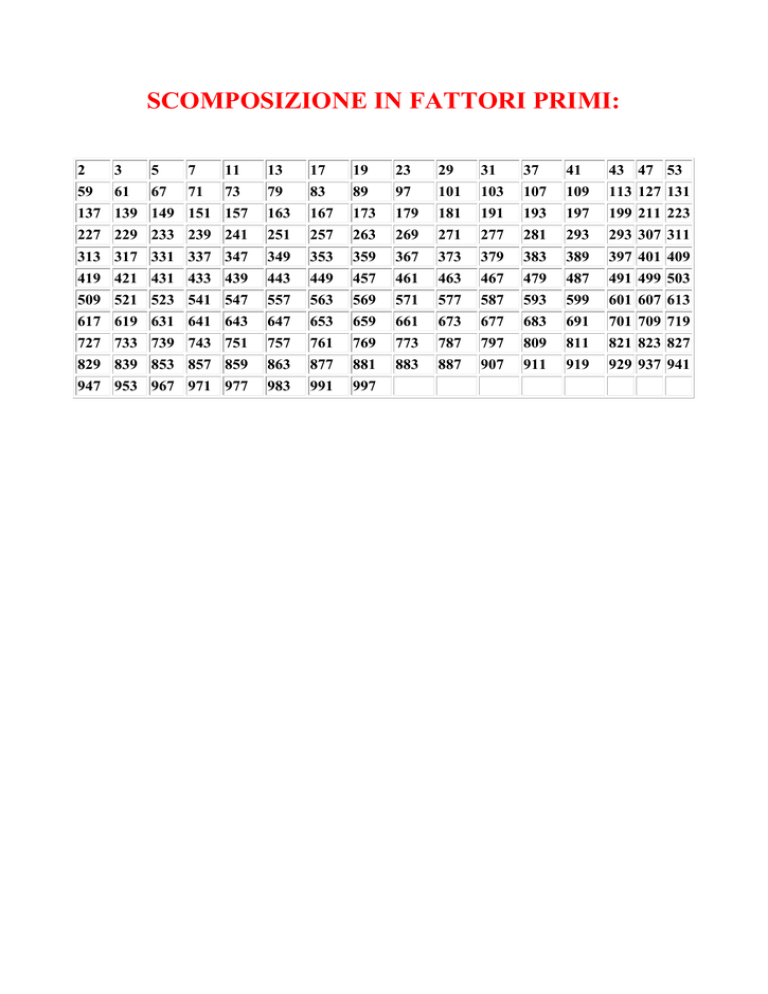
SCOMPOSIZIONE IN FATTORI PRIMI:
2
3
5
7
11
13
17
19
23
29
31
37
41
43 47 53
59
61
67
71
73
79
83
89
97
101
103
107
109
113 127 131
137 139 149 151 157
163
167
173
179
181
191
193
197
199 211 223
227 229 233 239 241
251
257
263
269
271
277
281
293
293 307 311
313 317 331 337 347
349
353
359
367
373
379
383
389
397 401 409
419 421 431 433 439
443
449
457
461
463
467
479
487
491 499 503
509 521 523 541 547
557
563
569
571
577
587
593
599
601 607 613
617 619 631 641 643
647
653
659
661
673
677
683
691
701 709 719
727 733 739 743 751
757
761
769
773
787
797
809
811
821 823 827
829 839 853 857 859
863
877
881
883
887
907
911
919
929 937 941
947 953 967 971 977
983
991
997
Prendiamo due numeri : 8 e 13.
Sappiamo che un numero è DIVISIBILE per un altro se eseguendo la DIVISIONE del primo per il secondo,
il RESTO è ZERO.
Ora il numero 8 è divisibile per:
1, 2, 4, 8.
Esaminiamo il numero 13. Esso è divisibile solamente per:
1, 13.
Quindi, 8 ammette come divisori 1, se stesso e altri divisori (2, 4).
Mentre 13 ammette come divisori solamente 1 e se stesso. I numeri come il 13 si chiamano NUMERI PRIMI
ASSOLUTI o più semplicemente NUMERI PRIMI.
Possiamo affermare che un NUMERO PRIMO è un numero DIVISIBILE solamente per 1 e per SE STESSO.
Si chiamano COMPOSTI, invece, i numeri che hanno, oltre all'uno e a se stessi, ALTRI DIVISORI.
Quindi:
NUMERO
DIVISORI
8
1, 2, 4, 8
NUMERO COMPOSTO
13
1, 13
NUMERO PRIMO
Facciamo degli altri esempi:
NUMERO
DIVISORI
11
1, 11
NUMERO PRIMO
105
1, 3, 5, 7, 21, 35, 105
NUMERO COMPOSTO
28
1, 2, 4, 7, 14, 28
NUMERO COMPOSTO
7
1, 7
NUMERO PRIMO
Il numero 1 non viene considerato nè un numero primo (in quanto ammette un solo divisore, se stesso), nè un numero
composto.
I NUMERI PARI, ad eccezione del numero 2, sono sempre dei NUMERI COMPOSTI perché ammettono come
divisori, sempre, oltre a se stessi e all'unità anche il 2.
Esempio:
NUMERO DIVISORI
4
1, 2, 4
6
1, 2, 3, 6
8
1, 2, 4, 8
10
1, 2, 5, 10
12
1, 2, 3, 4, 6, 12
Quindi i NUMERI PRIMI sono sicuramente NUMERI DISPARI.
Non è vero, invece, il contrario: cioè iNUMERI DISPARI non è detto che siano NUMERI PRIMI, quindi possono
essere sia NUMERI PRIMI che NUMERI COMPOSTI.
Esempio:
NUMERO
DIVISORI
3
1, 3
NUMERO PRIMO
5
1, 5
NUMERO PRIMO
7
1, 7
NUMERO PRIMO
9
1, 3, 9
NUMERO COMPOSTO
11
1, 11
NUMERO PRIMO
13
1, 13
NUMERO PRIMO
15
1, 3, 5, 15
NUMERO COMPOSTO
Quindi, ricapitolando:
1
non è nè NUMERO PRIMO nè NUMERO COMPOSTO
NUMERI PARI (eccetto il 2)
sono sempre NUMERI COMPOSTI
NUMERI DISPARI
possono essere NUMERI PRIMI o NUMERI COMPOSTI
I NUMERI PRIMI sono in numero ILLIMITATO infatti, se prendiamo un numero primo ne possiamo trovare
sempre uno maggiore.
Come sappiamo un NUMERO si dice COMPOSTO quando ha qualche altro divisore oltre all'UNITA' e a SE
STESSO.
Sappiamo anche che i NUMERI PARI sono senz'altro dei NUMERI COMPOSTI, mentre i numeri dispari possono
essere sia composti che primi.
Scegliamo, quindi, un numero pari, ad esempio:
30.
Esso è senz'altro un numero composto e ammette, come divisore, il 2.
Dividiamo allora per 2 e avremo:
30 : 2 = 15.
Di conseguenza possiamo scrivere:
15 x 2 = 30.
Anche 15 è un numero composto. Esso ha come più piccolo divisore il numero 3.
Quindi possiamo scrivere:
15 : 3 = 5.
E di conseguenza possiamo dire che:
3 x 5 = 15.
Quindi attraverso una serie di sostituzioni possiamo dire che: 30 = 2 x 15 = 2 x 3 x 5.
Ricapitolando:
30 = 2 x 3 x 5.
Come possiamo notare abbiamo scritto il numero 30 come il prodotto di più numeri e questi numeri (2, 3, 5) sono
tutti NUMERI PRIMI. Questa operazione prende il nome di SCOMPOSIZIONE di un NUMERO in FATTORI
PRIMI.
Quindi noi abbiamo scomposto 30 in fattori primi.
Prendiamo un altro NUMERO COMPOSTO, ad esempio: 105.
Il numero 105 non è divisibile per 2, trattandosi di un numero dispari.
E' divisibile per tre dato che la somma delle sue cifre è 6, cioè un numero divisibile per 3.
Quindi possiamo scrivere:
105 : 3 = 35.
Ovvero:
105 = 3 x 35.
Il numero 35 è ancora un numero composto che, poiché termina con la cifra 5, è divisibile per 5.
Quindi:
35 : 5 = 7.
Ovvero:
35 = 5 x 7.
Quindi possiamo dire che:
105 = 3 x 5 x 7.
Possiamo allora affermare che ogni NUMERO COMPOSTO è uguale al PRODOTTO di più NUMERI PRIMI.
Vediamo come si effettua, in pratica, la SCOMPOSIZIONE di un NUMERO in FATTORI PRIMI.
Prendiamo il numero 60 e proviamo a scomporlo in fattori primi.
Per fare questo dobbiamo tracciare una LINEA VERTICALE.
A sinistra di questa linea scriviamo il numero da scomporre, nel nostro caso60.
Ora cerchiamo il PIU' PICCOLO NUMERO PRIMO per cui esso è divisibile. Essendo il numero da scomporre 60,
cioè un numero pari, esso è senz'altro divisibile per 2.
Scriviamo questo fattore primo alla destra della linea verticale. Così:
Ora dividiamo 60 per 2 e scriviamo il risultato della divisione (cioè il quoto) sotto il numero 60. Così:
Cerchiamo ora il PIU' PICCOLO NUMERO PRIMO per cui è divisibile 30: anche in questo caso ci troviamo di
fronte ad un numero pari che sarà, quindi, divisibile per 2.
Scriviamo il 2 a destra del numero 30.
Ora dividiamo 30 per 2 e scriviamo il risultato della divisione sotto il numero 30. Così:
15 è un numero dispari, quindi non è certamente divisibile per 2. Esso invece è divisibile per 3, dato che la somma
delle sue cifre (1+5) dà come risultato 6 che è un numero divisibile per 3.
Scriviamo il 3 a destra del numero 15.
Ora dividiamo 15 per 3 e scriviamo il risultato della divisione sotto il numero 15.
Il numero 5 è un numero primo, divisibile solo per se stesso e per l'unità. Dividiamo allora il numero 5 per se stesso.
Il risultato della divisione è 1.
La nostra scomposizione del numero 60 in fattori primi è terminata.
Il NUMERO DA SCOMPORRE (nel nostro caso 60) può essere scritto come il PRODOTTO di tutti i FATTORI
PRIMI scritti a sinistra della linea verticale. Così:
60 = 2 x 2 x 3 x 5.
Ma sappiamo che
2 x 2 = 22.
Per cui sostituendo, avremo:
60 = 22 x 3 x 5.
Più in generale possiamo dire che per SCOMPORRE un numero in FATTORI PRIMI, lo si DIVIDE per il PIU'
PICCOLO NUMERO PRIMO SUO DIVISORE, poi si DIVIDE il QUOTO ottenuto per il PIU' PICCOLO
NUMERO PRIMO SUO DIVISORE, e così via fino ad ottenere come quoto 1.
Il numero dato è uguale al PRODOTTO di TUTTI I NUMERI PRIMI usati come DIVISORI.
Vediamo qualche altro esempio. Scomponiamo il numero
325.
Avremo:
Quindi possiamo scrivere:
325 = 5 x 5 x 13.
Ovvero:
325 = 52 x 13.
Ora scomponiamo il numero
168.
Avremo:
Quindi possiamo scrivere:
168 = 2 x 2 x 2 x 3 x 7.
Ovvero:
168 = 23 x 3 x 7.
Quando scriviamo un numero come prodotto di più numeri primi si parla di FATTORIZZAZIONE in NUMERI
PRIMI.
In alcuni casi è possibile abbreviare la scomposizione in fattori primi.
Vedremo, di seguito, come è possibile abbreviare, in alcuni casi, la SCOMPOSIZIONE di un numero in FATTORI
PRIMI.
Le regole che vedremo di seguito si fondano sui criteri di divisibilità di un numero.
1° REGOLA. Sappiamo che un numero è DIVISIBILE per10, 100, 1.000, ecc.. se esso TERMINA
rispettivamente con 1, 2, 3, .... ZERI.
Esempio:
1.350
Termina con uno zero
DIVISIBILE PER 10
1.800
Termina con due zeri
DIVISIBILE PER 100
27.000
Termina con tre zeri
DIVISIBILE PER 1.000
30.000
Termina con quattro zeri
DIVISIBILE PER 10.000
Poiché sappiamo che:
10 = 2 x 5;
100 = 22 x 52;
1.000 = 23 x 53;
ecc..
quando ci troviamo di fronte ad un numero divisibile per 10, 100, 1.000, ecc.., il PRIMO DIVISORE del numero sarà
rispettivamente: 2 x 5; 22 x 52; 23 x 53.
Esempio:
Per cui scriveremo:
1.350 = 2 x 5 x 33 x 5.
ovvero:
1.350 = 2 x 52 x 33.
Oppure
Per cui scriveremo:
1.800 = 23 x 52 x 32.
2° REGOLA. Sappiamo che un numero è DIVISIBILE per 4 se le sue ULTIME DUE CIFRE A DESTRA
formano un NUMERO DIVISIBILE per 4 o sono ENTRAMBI ZERO.
Esempio:
216
Ultime due cifre a destra 16
1.200
Ultime due cifre 00
Poiché sappiamo che:
16 divisibile per 4
216 DIVISIBILE PER 4
1.200 DIVISIBILE PER
4
4 = 22
quando ci troviamo di fronte ad un numero divisibile per 4, possiamo considerare come suo divisore 22.
Esempio:
Per cui scriveremo:
216 = 23 x 33.
Oppure:
Per cui scriveremo:
1.200 = 24 x 52 x 3.
3° REGOLA. Sappiamo che un numero è DIVISIBILE per 9se la SOMMA delle SUE CIFRE è
DIVISIBILE per 9.
Esempio:
Numero
Somma delle cifre
64.800
6 + 4 + 8 + 0 + 0 = 18
18 divisibile per 9
64.800 DIVISIBILE PER 9
Poiché sappiamo che: 9 = 32
quando ci troviamo di fronte ad un numero divisibile per 9, possiamo considerare come suo divisore 32.
Esempio:
Per cui scriveremo:
64.800 = 25 x 34 x 52.
CRITERI DI DIVISIBILITÀ
Un numero è DIVISIBILE per un altro se eseguendo la DIVISIONEdel primo per il
secondo, il RESTO è ZERO.
Cioè:
In questo caso possiamo dire che a è DIVISIBILE per b.
Esempio:
25 : 5 = 5 con resto 0
18 : 3 = 6 con resto 0
70 : 4 = 17 con resto 2
25 è DIVISIBILE per 5
18 è DIVISIBILE per 3
70 NON è DIVISIBILE per 4
Per sapere se un numero è divisibile per un altro non è sempre necessario eseguire la
divisione. Infatti, esistono delle REGOLE che ci permettono di stabilire facilmente se
un NUMERO E' DIVISIBILE per UN ALTRO. Queste regole prendono il nome
di CRITERI DI DIVISIBILITA'.
Vediamo, di seguito, quali sono questi criteri.
1. CRITERIO DI DIVISIBILITA' PER 2. Un numero è DIVISIBILE per 2 se la
sua ULTIMA CIFRA A DESTRA è 2 o una CIFRA PARI.
Esempio:
42
Ultima cifra a destra è 2
DIVISIBILE PER 2
172
Ultima cifra a destra è 2
DIVISIBILE PER 2
1.732
Ultima cifra a destra è 2
DIVISIBILE PER 2
874
Ultima cifra a destra è pari
DIVISIBILE PER 2
910
Ultima cifra a destra è pari.Lo zero è una cifra pari
DIVISIBILE PER 2
93
Ultima cifra a destra è dispari
NON DIVISIBILE PER 2
2. CRITERIO DI DIVISIBILITA' PER 3. Un numero è DIVISIBILE per 3 se
la SOMMA delle SUE CIFRE è DIVISIBILE per 3.
Esempio:
Numero Somma delle cifre
27
2+7=9
9 divisibile per 3
27 DIVISIBILE PER 3
147
1 + 4 + 7 = 12
12 divisibile per 3
147 DIVISIBILE PER 3
1.824
1 + 8 + 2 + 4 = 15
15 divisibile per 3
1.824 DIVISIBILE PER 3
337
3 + 3 + 7 = 13
13 non divisibile per 3
337 NON DIVISIBILE
PER 3
3. CRITERIO DI DIVISIBILITA' PER 4. Un numero è DIVISIBILE per 4 se le
sue ULTIME DUE CIFRE A DESTRA formano un NUMERO DIVISIBILE
per 4 o sono ENTRAMBI ZERO.
Esempio:
212
Ultime due cifre a destra 12
12 divisibile per 4
212 DIVISIBILE PER 4
1.316
Ultime due cifre a destra 16
16 divisibile per 4
1.316 DIVISIBILE PER 4
328
Ultime due cifre a destra 28
28 divisibile per 4
328 DIVISIBILE PER 4
100
Ultime due cifre a destra 00
937
Ultime due cifre a destra 37
DIVISIBILE PER 4
37 non divisibile per 4
937 NON DIVISIBILE PER 4
4. CRITERIO DI DIVISIBILITA' PER 5. Un numero è DIVISIBILE per 5 se
l'ULTIMA CIFRA A DESTRA è 5 o ZERO.
Esempio:
35
Ultima cifra a destra è 5
DIVISIBILE PER 5
185
Ultima cifra a destra è 5
DIVISIBILE PER 5
1.925
Ultima cifra a destra è 5
DIVISIBILE PER 5
210
Ultima cifra a destra è zero
DIVISIBILE PER 5
88
Ultima cifra a destra non è 5 nè 0
NON DIVISIBILE PER 5
5. CRITERIO DI DIVISIBILITA' PER 6. Un numero è DIVISIBILE per 6 se è
DIVISIBILE CONTEMPORANEAMENTE per 2 e per 3.
Esempio:
72
Ultima cifra a destra è pari. DIVISIBILE PER 2
DIVISIBILE PER 6
7 + 2 = 9. DIVISIBILE PER 3
792
Ultima cifra a destra è pari. DIVISIBILE PER 2
DIVISIBILE PER 6
7 + 9 + 2 = 18. DIVISIBILE PER 3
210
Ultima cifra a destra è pari. DIVISIBILE PER 2
DIVISIBILE PER 6
2 + 1 + 0 = 3. DIVISIBILE PER 3
88
Ultima cifra a destra è pari. DIVISIBILE PER 2
NON DIVISIBILE PER 6
8 + 8 = 16. NON DIVISIBILE PER 3
6. CRITERIO DI DIVISIBILITA' PER 9. Un numero è DIVISIBILE per 9 se la
SOMMA delle SUE CIFRE è DIVISIBILE per 9.
Esempio:
Numero Somma delle cifre
279
2 + 7 + 9 = 18
18 divisibile per 9
279 DIVISIBILE PER 9
972
9 + 7 + 2 = 18
18 divisibile per 9
972 DIVISIBILE PER 9
908
9 + 0 + 8 = 17
17 non divisibile per 9
908 NON DIVISIBILE PER
9
7. CRITERIO DI DIVISIBILITA' PER 10, 100, 1.000, ecc.... Un numero
è DIVISIBILE per 10, 100, 1.000, ecc.. se esso TERMINA rispettivamente con
1, 2, 3, .... ZERI.
Esempio:
1.250
Termina con uno zero
DIVISIBILE PER 10
13.520
Termina con uno zero
DIVISIBILE PER 10
12.200
Termina con due zeri
DIVISIBILE PER 100
135.700
Termina con due zeri
DIVISIBILE PER 100
12.000
Termina con tre zeri
DIVISIBILE PER 1.000
170.000
Termina con quattro zeri
DIVISIBILE PER 10.000
8. CRITERIO DI DIVISIBILITA' PER 11. Un numero è DIVISIBILE per 11 se
la DIFFERENZA tra la SOMMA delle CIFRE di posto DISPARI e
la SOMMA delle SUE CIFRE di posto PARI è uguale a ZERO,
o 11 o MULTIPLO di 11.
Esempio:
Numero Cifre di posto
dispari
Cifre di posto pari Somma cifre di posto Somma cifre di
dispari (a)
posto pari (b)
(a)
(b)
385
3, 5
8
3+5 = 8
8
8- DIVISIBILE
8= PER 11
0
77.132
7,1,2
7, 3
7+1+ 2 = 10
7+3 = 10
10- DIVISIBILE
10= PER 11
0
737
7, 7
3
7+7 = 14
3
14- DIVISIBILE
3= PER 11
11
2,1,8
8+9+7+9 = 33
2+1+8 = 11
33- DIVISIBILE
11= PER 11
22
8.291.789 8,9,7,9