piano di lavoro

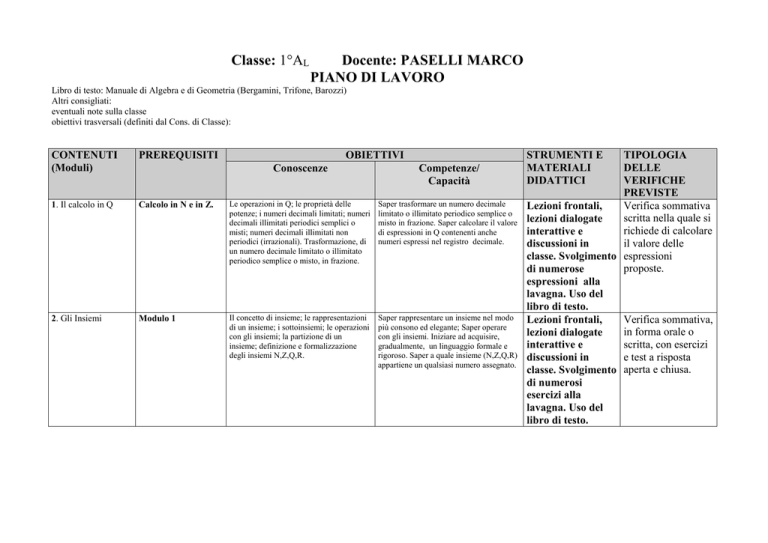
Classe: 1°AL
Docente: PASELLI MARCO
PIANO DI LAVORO
Libro di testo: Manuale di Algebra e di Geometria (Bergamini, Trifone, Barozzi)
Altri consigliati:
eventuali note sulla classe
obiettivi trasversali (definiti dal Cons. di Classe):
CONTENUTI
(Moduli)
PREREQUISITI
1. Il calcolo in Q
2. Gli Insiemi
OBIETTIVI
Conoscenze
Competenze/
Capacità
Calcolo in N e in Z.
Le operazioni in Q; le proprietà delle
potenze; i numeri decimali limitati; numeri
decimali illimitati periodici semplici o
misti; numeri decimali illimitati non
periodici (irrazionali). Trasformazione, di
un numero decimale limitato o illimitato
periodico semplice o misto, in frazione.
Saper trasformare un numero decimale
limitato o illimitato periodico semplice o
misto in frazione. Saper calcolare il valore
di espressioni in Q contenenti anche
numeri espressi nel registro decimale.
Modulo 1
Il concetto di insieme; le rappresentazioni
di un insieme; i sottoinsiemi; le operazioni
con gli insiemi; la partizione di un
insieme; definizione e formalizzazione
degli insiemi N,Z,Q,R.
Saper rappresentare un insieme nel modo
più consono ed elegante; Saper operare
con gli insiemi. Iniziare ad acquisire,
gradualmente, un linguaggio formale e
rigoroso. Saper a quale insieme (N,Z,Q,R)
appartiene un qualsiasi numero assegnato.
STRUMENTI E
MATERIALI
DIDATTICI
TIPOLOGIA
DELLE
VERIFICHE
PREVISTE
Verifica sommativa
Lezioni frontali,
scritta nella quale si
lezioni dialogate
richiede di calcolare
interattive e
il valore delle
discussioni in
classe. Svolgimento espressioni
proposte.
di numerose
espressioni alla
lavagna. Uso del
libro di testo.
Verifica sommativa,
Lezioni frontali,
in forma orale o
lezioni dialogate
scritta, con esercizi
interattive e
e test a risposta
discussioni in
classe. Svolgimento aperta e chiusa.
di numerosi
esercizi alla
lavagna. Uso del
libro di testo.
3. La Logica
Modulo 2
Il concetto di proposizione logica, e di
variabile logica; i connettivi logici e le
espressioni logiche; le tavole di verità; le
tautologie e le contraddizioni;
l’equivalenza di espressioni logiche; le
proprietà dei connettivi logici; la logica e
gli insiemi; i connettivi logici e gli insiemi;
i quantificatori.
Saper valutare il valore di verità di una
proposizione; saper stabilire l’equivalenza
di due proposizioni logiche; acquisire un
linguaggio rigoroso grazie ai
quantificatori, insiemistica e connettivi
logici; saper individuare e argomentare le
profonde connessioni e sinergie esistenti
tra logica ed insiemistica. Saper applicare
alla vita reale i concetti logici studiati, cioè
saper la matematica del cittadino.
4. I Monomi e i
Polinomi
Modulo 1
I monomi, le operazioni con i monomi,
massimo comune divisore e minimo
comune multiplo fra monomi; i polinomi;
le operazioni con i polinomi; i prodotti
notevoli; il triangolo di Tartaglia; il
principio d’identità dei polinomi; la
divisione tra polinomi; la regola di Ruffini;
il teorema del resto; il teorema di Ruffini;
Saper semplificare qualsiasi espressione
algebrica letterale. Saper determinare il
quoziente e il resto tra due polinomi. Saper
determinare il quoziente e il resto tra un
polinomio e un binomio monico o non
monico mediante la regola di Ruffini.
Saper calcolare la potenza n-esima di un
binomio sfruttando il triangolo di
Tartaglia.
5. Geometria: La
Geometria del piano
Modulo 1
La Geometria Euclidea.Gli enti primitivi,
la differenza tra postulati, definizioni,
lemmi, teoremi, corollari e concetto di
dimostrazione di un enunciato. I postulati
di appartenenza, il postulato dell’ordine.
Le semirette, i segmenti, le poligonali, i
semipiani, gli angoli; il movimento rigido,
la differenza tra uguaglianza e congruenza.
I cinque postulati di Euclide; le operazioni
con i segmenti; le operazioni con gli
angoli.
Saper eseguire le operazioni con segmenti
ed angoli; saper confrontare segmenti ed
angoli; saper costruire figure dalla sua
descrizione e viceversa; saper fare
semplici dimostrazioni di enunciati.
Lezioni frontali,
lezioni dialogate
interattive e
discussioni in
classe. Svolgimento
di numerosi
esercizi alla
lavagna. Uso del
libro di testo.
Lezioni frontali,
lezioni dialogate
interattive e
discussioni in
classe. Svolgimento
di numerosi
esercizi alla
lavagna. Uso del
libro di testo.
Lezioni frontali,
lezioni dialogate
interattive, lavoro
di gruppo e
discussioni in
classe. Svolgimento
di numerosi
esercizi e
dimostrazioni alla
lavagna. Uso del
libro di testo.
Verifica sommativa,
in forma orale o
scritta, con esercizi
e test a risposta
aperta e chiusa.
Verifica sommativa,
in forma orale o
scritta, con esercizi
da svolgere.
Verifica sommativa,
in forma orale o
scritta, nella quale si
richiede la
dimostrazione di
particolari
enunciati.
6. La scomposizione
in fattori e le frazioni
algebriche
Modulo 4
Il raccoglimento a fattore comune totale e
parziale; la scomposizione riconducibile a
prodotti notevoli; la scomposizione del
trinomio di secondo grado monico e non
monico; la scomposizione mediante il
teorema e la regola di Ruffini; il M.C.D. e
il m.c.m. fra polinomi. Le frazioni
algebriche; le condizioni di esistenza delle
frazioni algebriche; il calcolo con le
frazioni algebriche;
Saper scomporre in fattori polinomi
assegnati; saper determinare il M.C.D. e il
m.c.m. fra polinomi e saper eseguire le
operazioni con le frazioni algebriche.
7. Geometria: I
triangoli
Modulo 5
La definizione di triangolo, e
Saper effettuare dimostrazioni, anche non
considerazioni generali, bisettrici, mediane banali, di enunciati nei quali intervengono
e altezze di un triangolo; la classificazione anche triangoli.
dei triangoli; Il primo e il Secondo Criterio
di Congruenza dei Triangoli; Le proprietà
del triangolo isoscele ed equilatero; Il terzo
Criterio di Congruenza dei Triangoli; le
disuguaglianze nei triangoli;
8. Le equazioni
lineari
Modulo 6 ed elementi
di geometria piana e
solida delle scuole
medie inferiori
Le identità, le equazioni, le soluzioni di
un’equazione, i diversi tipi di equazioni;
forma normale di un’equazione e il suo
grado; i principi di equivalenza; le
applicazioni del primo e secondo principio
di equivalenza; le equazioni numeriche
intere; la risoluzione di un’equazione
numerica intera; equazioni determinate,
indeterminate e impossibili; le equazioni
fratte; la risoluzione di un’equazione
numerica fratta; le equazioni letterali; la
risoluzione di un’equazione letterale
intera; la risoluzione di un’equazione
letterale fratta; equazioni e problemi.
Saper risolvere: equazioni numeriche
intere e fratte, equazioni letterali intere e
fratte. Saper risolvere problemi di vario
genere, in particolare geometrici, mediante
l’uso delle equazioni.
Verifica sommativa,
in forma orale o
scritta, nella quale si
richiede sia di
scomporre
polinomi, sia di
calcolare il m.c.m
tra polinomi, sia
infine di
semplificare
espressioni
contenenti frazioni
algebriche.
Verifica sommativa,
Lezioni frontali,
in forma orale o
lezioni dialogate
interattive, lavoro scritta, nella quale si
richiede la
di gruppo e
dimostrazione di
discussioni in
classe. Svolgimento particolari
enunciati.
di numerose
dimostrazioni alla
lavagna. Uso del
libro di testo.
Verifica sommativa,
Lezioni frontali,
in forma orale o
lezioni dialogate
interattive, lavoro scritta, nella quale si
richiede non solo di
di gruppo e
risolvere equazioni
discussioni in
classe. Svolgimento lineari, ma anche
problemi mediante
di numerose
l’uso di equazioni.
equazioni e
problemi alla
lavagna. Uso del
libro di testo.
Lezioni frontali,
lezioni dialogate
interattive, lavoro
di gruppo e
discussioni in
classe. Svolgimento
di numerosi
esercizi alla
lavagna. Uso del
libro di testo.
9. Geometria: Le
rette parallele e le
rette perpendicolari
Modulo 7
Le rette perpendicolari: il teorema
dell’esistenza e dell’unicità della
perpendicolare; le proiezioni ortogonali; la
distanza di un punto da una retta; l’asse di
un segmento. Le rette parallele: le rette
tagliate da una trasversale; il teorema delle
rette parallele; la parallela per un punto ad
una retta data; l’inverso del teorema delle
rette parallele. Le proprietà degli angoli
dei poligoni: il teorema dell’angolo
esterno; la somma degli angoli interni di
un triangolo; la somma degli angoli interni
di un poligono convesso; i criteri di
congruenza dei triangoli rettangoli;
Saper dimostrare enunciati contenenti tutti
gli argomenti affrontati nei moduli di
geometria (fino al 9)
10. Le Disequazioni
lineari
Modulo 8
Le disuguaglianze numeriche e relative
Saper risolvere disequazioni lineari
proprietà; le disequazioni di primo grado
numeriche intere, letterali intere e
intere; le disequazioni equivalenti; primo e numeriche fratte.
secondo principio di equivalenza; la
risoluzione di disequazioni di primo grado
intere numeriche e letterali; la
rappresentazione delle soluzioni; le
disequazioni numeriche fratte e relativa
risoluzione.
Lezioni frontali,
lezioni dialogate
interattive, lavoro
di gruppo e
discussioni in
classe. Svolgimento
di numerose
dimostrazioni alla
lavagna.Uso del
libro di testo.
Verifica sommativa,
in forma orale o
scritta, nella quale si
richiede la
dimostrazione di
particolari
enunciati.
Lezioni frontali,
lezioni dialogate
interattive, lavoro
di gruppo e
discussioni in
classe. Risoluzione
di numerose
disequazioni alla
lavagna. Uso del
libro di testo.
Verifica sommativa,
in forma orale o
scritta, nella quale si
richiede la
risoluzione di tutti i
tipi di disequazioni
lineari trattate.