VARIABILI CASUALI CONTINUE
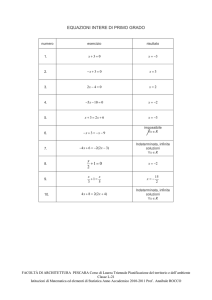
Una variabile casuale si dice continua quando il numero dei casi sotto i quali si può
presentare sono “infinitamente grandi”.
Quando la popolazione di riferimento è continua il concetto di unità che compongono
l’universo scompare; questo numero deve essere considerato infinito e di conseguenza
infinitesima ( prossima a zero) la frequenza della singola unità della popolazione.
Ha senso invece parlare di frequenza di unità comprese in una porzione continua e tale
frequenza verrà definita in termini di area .
Anche la probabilità pertanto viene definita in termini di area.
Esempio: si supponga di aver rilevato e suddiviso la statura espressa in cm in classi di
uguale ampiezza e di aver assegnato a ciascuna un livello di probabilità ( in termini di
frequenza dei casi osservati ).
statura
probabilità
140-150
151-160
161-170
171-180
181-190
191-200
201-210
totale
0,06
0,08
0,19
0,32
0,21
0,08
0,06
1
Ampiezza
classe
10
10
10
10
10
10
10
Densità =
probabilità/ampiezza classe
0,006
0,008
0,019
0,032
0,021
0,008
0,006
Area dei singoli
rettangoli
10·0,006=0,06
10·0,008=0,08
10·0,019=0,19
10·0,032=0,32
10·0,021=0,21
10·0,008=0,08
10·0,006=0,06
1
Questa distribuzione di probabilità si può rappresentare graficamente mediante un
istogramma : i rettangoli avranno pertanto per basi segmenti di lunghezza pari
all’ampiezza delle classi e altezze uguali alle densità.
In questo modo l’altezza del singolo rettangolo esprime la densità di probabilità e l’area del
rettangolo le probabilità associata alla classe.
La somma delle aree dei rettangoli è uguale a 1 .
0,035
0,03
0,025
densità
0,02
0,015
0,01
0,005
0
141-150
151-160
161-170
171-180
181-190
191-200
201-210
classi d i statura
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 1 di 23
Se si prendono classi di ampiezza sempre più piccole si hanno altri istogrammi che hanno
un grafico molto più regolare:
0,12000
0,10000
0,08000
0,06000
0,04000
0,02000
12
212
5
12
612
9
13
013
3
13
413
7
13
814
1
14
214
5
14
614
9
15
01
53
15
415
7
15
816
1
16
216
5
16
616
9
17
017
3
17
417
7
17
818
1
18
218
5
18
618
9
19
019
3
19
419
7
19
820
1
20
220
5
20
620
9
0,00000
-0,02000
Riducendo sempre più le classi , la spezzata a tratti orizzontale che delimita
superiormente l’istogramma tende ad identificarsi con una curva continua.
Indicato con f(x) la funzione di densità corrispondente al generico valore di x sull’ascissa (
si ricorda che la funzione di densità corrisponde al valore assunto dall’altezza del
rettangolo) , questo valore nella curva è infinitesimo, cioè tende ad essere uguale a zero.
La probabilità, nelle distribuzioni continue, viene definita in termini di area compresa tra
due estremi a e b e si indica con l’espressione
P(a < X ≤ b) = F (b) − F (a )
e indica la probabilità che la variabile casuale X assume un valore compreso tra a e b .
La probabilità in un punto è nulla.
0,12000
0,10000
0,08000
AREA SOTTESA
AI VALORI a e b
0,06000
0,04000
0,02000
0,00000
12
212
5
12
612
9
13
013
3
13
413
7
13
814
1
14
214
5
14
614
9
15
01
53
15
415
7
15
816
1
16
216
5
16
616
9
17
017
3
17
417
7
17
818
1
18
218
5
18
618
9
19
019
3
19
419
7
19
820
1
20
220
5
20
620
9
a
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 2 di 23
LA DISTRIBUZIONE NORMALE O DI GAUSS
Considerato un collettivo numeroso, le modalità xi assunte da una carattere quantitativo
X rappresentano una variabile con valori generalmente tutti diversi, ma con la costanza
che essi tendono ad addensarsi intorno al proprio valore medio. Gli scarti delle modalità
_
dalla media xi − x , assimilabili ad errori accidentali ( errori dovuti a numerose piccole
cause non sempre facilmente controllabili e determinabili ) presentano una certa regolarità
di comportamento:
a) gli scarti positivi sono frequenti quanto gli scarti negativi;
b) gli scarti piccoli hanno frequenza elevata che diminuisce via via che gli scarti
diventano più grandi.
La rappresentazione grafica di tali valori darà luogo ad una curva campanulare ,
simmetrica rispetto alla media e con andamento decrescente su entrambi i lati man mano
che gli scarti diventano più estesi.
La curva normale o di Gauss ( il matematico tedesco che ha scoperto la curva ) ha la
seguente distribuzione di probabilità:
Y=
1
σ ⋅ 2π
⋅e
-
µ è la media aritmetica del collettivo;
-
σ è lo scarto quadratico medio;
-
π = 3,14159… ;
-
e = 2,71828… è il numero neperiano.
−
( xi − µ ) 2
2σ 2
dove
Dallo studio della funzione si rilevano le seguenti caratteristiche della curva:
a) la forma è campanulare, è unimodale ed è simmetrica rispetto alla media;
b) moda, mediana e media coincidono;
c) presenta due punti di flesso ( cambio di curvatura della funzione ) in corrispondenza
dei valori u ± σ ;
d) tende a zero ( Y → 0 ) quanto più ci si allontana dalla media;
e) nell’intervallo u ± σ
è compreso il 68,27% delle frequenze dei casi rilevati,
nell’intervallo u ± 2σ è compreso il 95,45% delle frequenze dei casi rilevati,
nell’intervallo
u ± 3σ è compreso il 99,73% delle frequenze dei casi rilevati; le due
aree di coda dopo l’ultimo intervallo raccolgono in totale solo lo 0,27% dei casi
rilevati.
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 3 di 23
L’area della curva per valori delle modalità xi che spaziano da − ∞ a + ∞ è uguale a 1.
La curva dipende , è definita completamente, solo dai due parametri media e varianza;
esistono, pertanto, infinite curve normali descritte dalle possibili coppie (u; σ 2 ) .
In particolare:
-
cambiando la media della distribuzione, la curva si sposta sull’asse delle ascisse, verso
destra se la media aumenta, verso sinistra se la media diminuisce;
-
cambiando la varianza della distribuzione , se la variabilità intorno alla media aumenta
la forma della curva è più appiattita , se la variabilità diminuisce la forma è più
appuntita.
La variabile casuale normale si indica con l’espressione N (u; σ 2 ) .
Anziché descrivere e calcolare le probabilità di infinite curve normali con diverse medie e
variabilità si ricorre alla variabile normale standardizzata.
DISTRIBUZIONE NORMALE STANDARDIZZATA
xi − u
Indicato con zi =
σ
lo scarto standardizzato , si dimostra che la normale N (u; σ 2 )
diventa una normale con media uguale a zero e varianza uguale a uno e si indica con
l’espressione
N (0;1)
,
normale
standardizzata
con
funzione
di
probabilità
2
z
−
1
Y (Z ) =
⋅ e 2 ; essa dipende solo dai valori standardizzati zi .
2π
Graficamente la media originaria u viene a coincidere con l’origine degli assi e i punti di
flesso con i valori ± 1.
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 4 di 23
Conseguentemente gli intervalli u ± kσ diventano 0 ± k1 e l’area sottesa sarà del 68,27%
tra (− 1;+1) , del 95,45% tra (− 2;+2 ) e del 99,73% tra (− 3;+3) .
Fatta questa trasformazione si possono usare le tavole della normale standardizzata
( tavola A ) . I valori della tabella indicano la proporzione dei casi che cadono nell’intervallo
(0; z ) e si indicano con l’espressione F ( z ) = P (0 < Z < z ) , area di probabilità compresa tra
zero e il valore standardizzato z .
probabilità che la variabile
casuale assuma i valori tra 0 e z
Noto il valore xi lo si standardizza con la formula z =
xi − u
σ
e si ottiene il valore di z ; dalle
tavole si scorre la prima colonna fino a trovare il valore di z più vicino a quello
standardizzato; sulla stessa riga , seconda colonna , si hanno i valori F ( z ) = P (0 < Z < z )
corrispondenti all’area di probabilità tra 0 e z .
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 5 di 23
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 6 di 23
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 7 di 23
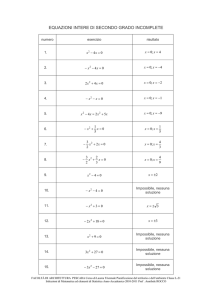
ESERCIZI SULLA DISTRIBUZIONE NORMALE
1) Una variabile casuale ha distribuzione normale standardizzata. Calcolare le seguenti
probabilità:
a) P(0<Z<1,18);
b) P(0<Z<2,05);
c) P(-0,85<Z<0);
d) P(0,6<Z<2,53);
e) P(-2,45<Z<-0,51);
f) P(-2,3<Z<1,16);
g) P(-1<Z<2,5);
h) P(0,5<Z<2,5);
i) P(-3<Z<+3).
2) Trovare l’area sotto la curva normale standardizzata per ciascuno dei seguenti casi:
a) estremi z=0 e z=1,2;
b) estremi z=-0,68 e z=0;
c) estremi z=-0,46 e z=2,21;
d) estremi z=0,81 e z=1,94;
e) a sinistra di z=-0,6;
f) a destra di z=-1,28;
g) a destra di z=2,05 e a sinistra di z=-1,44.
3) Una variabile casuale ha distribuzione normale standardizzata. Calcolare le seguenti
probabilità:
a) P(Z ≥ 2,3);
b) P(Z ≥ 0,56);
c) P(Z ≥ -1,80);
d) P(Z ≤ -1,85);
e) P(Z ≤ 0,78);
f) P(Z ≤ 1,41).
4) Una variabile casuale ha distribuzione normale standardizzata. Determinare il valore
della variabile z, nota la probabilità:
a) P(Z ≤ z)=0,20;
b) P(Z ≤ z)=0,80;
c) P(- z <Z< + z)=0,75;
d) P(- z<Z<+ z)=0,99;
e) P(-0,80<Z< z)=0,6728;
f) P(z<Z<2,25)=0,3226;
5) Determinare il valore di z per i casi sotto elencati:
a) l’area compresa tra 0 e z vale 0,3770;
b) l’area a sinistra di z vale 0,8621;
c) l’area compresa tra –1,5 e z vale 0,0217;
d) l’area compresa tra z e –1,5 vale 0,0217.
6) Ad un esame finale di statistica , la media dei voti è stata di 72 e lo scarto quadratico
medio pari a 15. Determinare i valori standardizzati dei seguenti voti:
a) 60;
b) 93;
c) 72 .
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 8 di 23
7) Il voto medio e lo scarto quadratico medio dei voti di una simulazione di statistica sono
stati rispettivamente m=6,5 e s.q.m=1,5 determinare il punteggio in unità
standardizzate dei seguenti voti:
a) 8;
b) 7,5;
c) 3;
d) 6,5;
e) 9,3 ;
f) 5 .
8) Tenendo presente l’esercizio
standardizzati:
a) –1 ;
b) 1,6 ;
n.6
trovare i voti corrispondenti ai seguenti valori
9) Tenendo presente l’esercizio n.7 trovare i valori corrispondenti ai seguenti punteggi
standardizzati:
a) 1;
b) 0; c) 2 ; d) –2 .
10) Sia X una variabile a distribuzione normale con media 10 e varianza 9 . Calcolare la
probabilità:
a) P(7<X<12);
b) P(9<X<13);
c) P(11<X<15);
d) P(4<X<10);
e) P(X ≤ 8);
f) P(X ≤ 13);
g) P(X ≥ 18);
h) P(X ≥ 8,5).
11) Sia X una variabile a distribuzione normale con media 64 e varianza 16 . Calcolare la
probabilità che i valori della variabili risultino :
a) compresi fra 50 e 64;
b) compresi fra 50 e 60;
c) compresi fra 70 e 80;
d) non minori di 50;
e) non maggiori di 62;
f) maggiori di 64.
12) I pesi di 1.000 soldati di leva sono distribuiti normalmente con valore medio 70 kg e
s.q.m. 8 kg. Determinare la probabilità dei seguenti eventi:
a) i pesi siano compresi fra 60 e 70 kg;
b) i pesi siano compresi tra 65 e 90 kg;
c) i pesi siano almeno 80 kg;
d) i pesi siano non più di 60;
e) calcolare quanti soldati hanno peso di almeno 75 kg e quanti hanno peso inferiore
ai 65 kg.
13) Una ditta produce sbarrette della lunghezza media di 1,50 cm con s.q.m. di 0,05 cm.
Sapendo che le lunghezze sono distribuite normalmente , calcolare la probabilità di
avere sbarre lunghe:
a) più di 1,62 cm;
b) meno di 1,45 cm;
c) fra 1,45 cm e 1,60 cm.
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 9 di 23
14) Una macchina produce sacchetti di caramelle del peso medio di 200 grammi con
s.q.m. di 10 grammi. Calcolare :
a) la percentuale di sacchetti che pesano più di 220 grammi;
b) la percentuale di sacchetti che pesano più di 190 grammi.
c) Se a un controllo vengono scartati i sacchetti con un peso inferiore a 185 grammi,
su 1.000 sacchetti prodotti quanti si prevede saranno scartati?
15) La vita media delle lavatrici prodotte da una ditta è di 10 anni, con uno scarto
quadratico medio di 4 anni. Calcolare, in un lotto di 500 lavatrici, quante:
a) saranno in vita dopo 16 anni;
b) avranno durata compresa fra 8 e 12 anni;
c) avranno durata inferiore agli 8 anni;
d) avranno durata uguale o superiore a 8 anni.
16) Sia X una variabile distribuita normalmente . Calcolare lo scarto quadratico medio
sapendo che P ( X ≥ 5,2) = 0,18 e u = 4 .
17) Ad un concorso finito il voto medio è stato 72 con s.q.m. 9. Il miglior 10% degli studenti
sarà vincitore. Qual è il voto minimo che uno studente deve ottenere per essere
vincitore del concorso?
18) Per l’assunzione in una ditta gli aspiranti devono superare un test attitudinale. Da
precedenti esperienze si sa che il voto medio riportato è 62 con s.q.m. 10 . Sapendo
che 1.500 persone si sottoporranno al test , determinare quante saranno assunte se il
voto minimo richiesto è 70. Se invece la ditta è disposta ad assumere 240 persone,
qual è il voto minimo per essere assunti?
19) Sia X una variabile distribuita normalmente. Noti due valori x1 = 8,5 e x 2 = 4 , con i
rispettivi scarti standardizzati z1 = 0,5 e z 2 = −1 determinare media e scarto quadratico
medio della variabile casuale.
20) Sia X una variabile distribuita normalmente . Calcolare media e scarto quadratico
medio sapendo che P ( X ≥ 10) = 0,30 e P ( X ≥ 15) = 0,06 .
21) In una partita di arance il peso delle singole arance è distribuito normalmente e in
seguito ad un campionamento si è trovato un valore medio pari a 2 hg con scarto
quadratico medio 0,15 hg . Valutare la probabilità che in quella partita si trovino arance
che pesano più di 2,55 hg.
22) Si è rilevato statisticamente che i neonati di una città hanno peso medio di 3.250 g con
s.q.m. di 300 g .
Ipotizzando che il peso sia normalmente distribuito, determinare:
a) quale percentuale di neonati ha peso superiore a 3.000 g;
b) quale percentuale di neonati ha peso inferiore a 2.500 g;
c) quale peso è superato dal 10% dei neonati.
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 10 di 23
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 11 di 23
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 12 di 23
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 13 di 23
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 14 di 23
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 15 di 23
z=0,67
z=1,867
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 16 di 23
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 17 di 23
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 18 di 23
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 19 di 23
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 20 di 23
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 21 di 23
TABELLA A Aree di probabilità sotto la curva normale standardizzata F(z)= P(0<Z<z)
valori
di z
F( z )
valori
di z
valori
valori
di
F(
di z
z)
valori
valori
di
F(
di z
z)
valori
valori
di
F(
di z
z)
valori
valori
di
F(
di z
z)
valori
valori
di
F(
di z
z)
valori
valori
di
F(
di z
z)
valori
di
F(
z)
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,1
0,11
0,12
0,13
0,14
0,15
0,16
0,17
0,18
0,19
0,2
0,21
0,22
0,23
0,24
0,25
0,26
0,27
0,28
0,29
0,3
0,31
0,32
0,33
0,34
0,35
0,36
0,37
0,38
0,39
0,4
0,41
0,42
0,43
0,44
0,45
0,46
0,47
0,48
0,49
0,50
0,0040
0,0080
0,0120
0,0160
0,0199
0,0239
0,0279
0,0319
0,0359
0,0398
0,0438
0,0478
0,0517
0,0557
0,0596
0,0636
0,0675
0,0714
0,0753
0,0793
0,0832
0,0871
0,0910
0,0948
0,0987
0,1026
0,1064
0,1103
0,1141
0,1179
0,1217
0,1255
0,1293
0,1331
0,1368
0,1406
0,1443
0,1480
0,1517
0,1554
0,1591
0,1628
0,1664
0,1700
0,1736
0,1772
0,1808
0,1844
0,1879
0,1915
0,51
0,52
0,53
0,54
0,55
0,56
0,57
0,58
0,59
0,6
0,61
0,62
0,63
0,64
0,65
0,66
0,67
0,68
0,69
0,7
0,71
0,72
0,73
0,74
0,75
0,76
0,77
0,78
0,79
0,8
0,81
0,82
0,83
0,84
0,85
0,86
0,87
0,88
0,89
0,9
0,91
0,92
0,93
0,94
0,95
0,96
0,97
0,98
0,99
1
0,1950
0,1985
0,2019
0,2054
0,2088
0,2123
0,2157
0,2190
0,2224
0,2257
0,2291
0,2324
0,2357
0,2389
0,2422
0,2454
0,2486
0,2517
0,2549
0,2580
0,2611
0,2642
0,2673
0,2704
0,2734
0,2764
0,2794
0,2823
0,2852
0,2881
0,2910
0,2939
0,2967
0,2995
0,3023
0,3051
0,3078
0,3106
0,3133
0,3159
0,3186
0,3212
0,3238
0,3264
0,3289
0,3315
0,3340
0,3365
0,3389
0,3413
0,3438
0,3461
0,3485
0,3508
0,3531
0,3554
0,3577
0,3599
0,3621
0,3643
0,3665
0,3686
0,3708
0,3729
0,3749
0,3770
0,3790
0,3810
0,3830
0,3849
0,3869
0,3888
0,3907
0,3925
0,3944
0,3962
0,3980
0,3997
0,4015
0,4032
0,4049
0,4066
0,4082
0,4099
0,4115
0,4131
0,4147
0,4162
0,4177
0,4192
0,4207
0,4222
0,4236
0,4251
0,4265
0,4279
0,4292
0,4306
0,4319
0,4332
0,4345
0,4357
0,4370
0,4382
0,4394
0,4406
0,4418
0,4429
0,4441
0,4452
0,4463
0,4474
0,4484
0,4495
0,4505
0,4515
0,4525
0,4535
0,4545
0,4554
0,4564
0,4573
0,4582
0,4591
0,4599
0,4608
0,4616
0,4625
0,4633
0,4641
0,4649
0,4656
0,4664
0,4671
0,4678
0,4686
0,4693
0,4699
0,4706
0,4713
0,4719
0,4726
0,4732
0,4738
0,4744
0,4750
0,4756
0,4761
0,4767
0,4772
0,4778
0,4783
0,4788
0,4793
0,4798
0,4803
0,4808
0,4812
0,4817
0,4821
0,4826
0,4830
0,4834
0,4838
0,4842
0,4846
0,4850
0,4854
0,4857
0,4861
0,4864
0,4868
0,4871
0,4875
0,4878
0,4881
0,4884
0,4887
0,4890
0,4893
0,4896
0,4898
0,4901
0,4904
0,4906
0,4909
0,4911
0,4913
0,4916
0,4918
0,4920
0,4922
0,4925
0,4927
0,4929
0,4931
0,4932
0,4934
0,4936
0,4938
0,4940
0,4941
0,4943
0,4945
0,4946
0,4948
0,4949
0,4951
0,4952
0,4953
0,4955
0,4956
0,4957
0,4959
0,4960
0,4961
0,4962
0,4963
0,4964
0,4965
0,4966
0,4967
0,4968
0,4969
0,4970
0,4971
0,4972
0,4973
0,4974
0,4974
0,4975
0,4976
0,4977
0,4977
0,4978
0,4979
0,4979
0,4980
0,4981
0,4981
0,4982
0,4982
0,4983
0,4984
0,4984
0,4985
0,4985
0,4986
0,4986
0,4987
0,4987
0,4987
0,4988
0,4988
0,4989
0,4989
0,4989
0,4990
0,4990
0,4990
0,4991
0,4991
0,4991
0,4992
0,4992
0,4992
0,4992
0,4993
0,4993
0,4993
0,4993
0,4994
0,4994
0,4994
0,4994
0,4994
0,4995
0,4995
0,4995
0,4995
0,4995
0,4995
0,4996
0,4996
0,4996
0,4996
0,4996
0,4996
0,4997
0,4997
0,4997
0,4997
0,4997
0,4997
0,4997
0,4997
0,4997
0,4997
0,4998
0,4998
0,4998
0,4998
0,4998
0,4998
0,4998
0,4998
0,4998
0,4998
0,4998
0,4998
0,4998
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,4999
0,5000
0,5000
0,5000
0,5000
0,5000
0,5000
0,5000
0,5000
0,5000
0,5000
0,5000
1,01
1,02
1,03
1,04
1,05
1,06
1,07
1,08
1,09
1,1
1,11
1,12
1,13
1,14
1,15
1,16
1,17
1,18
1,19
1,2
1,21
1,22
1,23
1,24
1,25
1,26
1,27
1,28
1,29
1,3
1,31
1,32
1,33
1,34
1,35
1,36
1,37
1,38
1,39
1,4
1,41
1,42
1,43
1,44
1,45
1,46
1,47
1,48
1,49
1,50
1,51
1,52
1,53
1,54
1,55
1,56
1,57
1,58
1,59
1,6
1,61
1,62
1,63
1,64
1,65
1,66
1,67
1,68
1,69
1,7
1,71
1,72
1,73
1,74
1,75
1,76
1,77
1,78
1,79
1,8
1,81
1,82
1,83
1,84
1,85
1,86
1,87
1,88
1,89
1,9
1,91
1,92
1,93
1,94
1,95
1,96
1,97
1,98
1,99
2
2,01
2,02
2,03
2,04
2,05
2,06
2,07
2,08
2,09
2,1
2,11
2,12
2,13
2,14
2,15
2,16
2,17
2,18
2,19
2,2
2,21
2,22
2,23
2,24
2,25
2,26
2,27
2,28
2,29
2,3
2,31
2,32
2,33
2,34
2,35
2,36
2,37
2,38
2,39
2,4
2,41
2,42
2,43
2,44
2,45
2,46
2,47
2,48
2,49
2,50
2,51
2,52
2,53
2,54
2,55
2,56
2,57
2,58
2,59
2,6
2,61
2,62
2,63
2,64
2,65
2,66
2,67
2,68
2,69
2,7
2,71
2,72
2,73
2,74
2,75
2,76
2,77
2,78
2,79
2,8
2,81
2,82
2,83
2,84
2,85
2,86
2,87
2,88
2,89
2,9
2,91
2,92
2,93
2,94
2,95
2,96
2,97
2,98
2,99
3
3,01
3,02
3,03
3,04
3,05
3,06
3,07
3,08
3,09
3,1
3,11
3,12
3,13
3,14
3,15
3,16
3,17
3,18
3,19
3,2
3,21
3,22
3,23
3,24
3,25
3,26
3,27
3,28
3,29
3,3
3,31
3,32
3,33
3,34
3,35
3,36
3,37
3,38
3,39
3,4
3,41
3,42
3,43
3,44
3,45
3,46
3,47
3,48
3,49
3,50
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 22 di 23
3,51
3,52
3,53
3,54
3,55
3,56
3,57
3,58
3,59
3,6
3,61
3,62
3,63
3,64
3,65
3,66
3,67
3,68
3,69
3,7
3,71
3,72
3,73
3,74
3,75
3,76
3,77
3,78
3,79
3,8
3,81
3,82
3,83
3,84
3,85
3,86
3,87
3,88
3,89
3,9
3,91
3,92
3,93
3,94
3,95
3,96
3,97
3,98
3,99
4
BIBLIOGRAFIA
Lezioni ed esercizi hanno trovato spunto ( o ripresi ) dai seguenti testi:
1.
2.
3.
4.
5.
6.
Gambotto Manzone – Consolini , matematica con applicazioni informatiche 2, Tramontana ;
Scaglianti, il modello non deterministico, CEDAM;
Spiegel, collana SCHAUM , statistica, Etas libri;
Trovato – Manfredi, calcolo delle probabilità e statistica inferenziale, Ghisetti e Corvi editori;
Girone – Sallustio, esercizi di statistica, Cacucci editore;
F. Di Giovanni, complementi ed esercizi di statistica, Facoltà Scienze Statistiche, UNIROMA.
FACOLTÀ DI ECONOMIA PESCARA Corso di Laurea Triennale in ECONOMIA E COMMERCIO Classe L-33
STATISTICA Anno Accademico 2010-2011 Prof . Annibale ROCCO
VARIABILI CASUALI CONTINUE Pagina 23 di 23