LA LEZIONE
Punti critici
Raccogliendo il vapore di un liquido in un contenitore molto resistente e mantenendolo
a temperatura costante si può osservare, aumentando la pressione, la formazione di
liquido con la presenza del caratteristico menisco a separare le due fasi. La
condensazione ottenuta per il solo aumento della pressione, non avviene però a tutte le
temperature. Al di sopra di un valore critico la sola compressione non può più
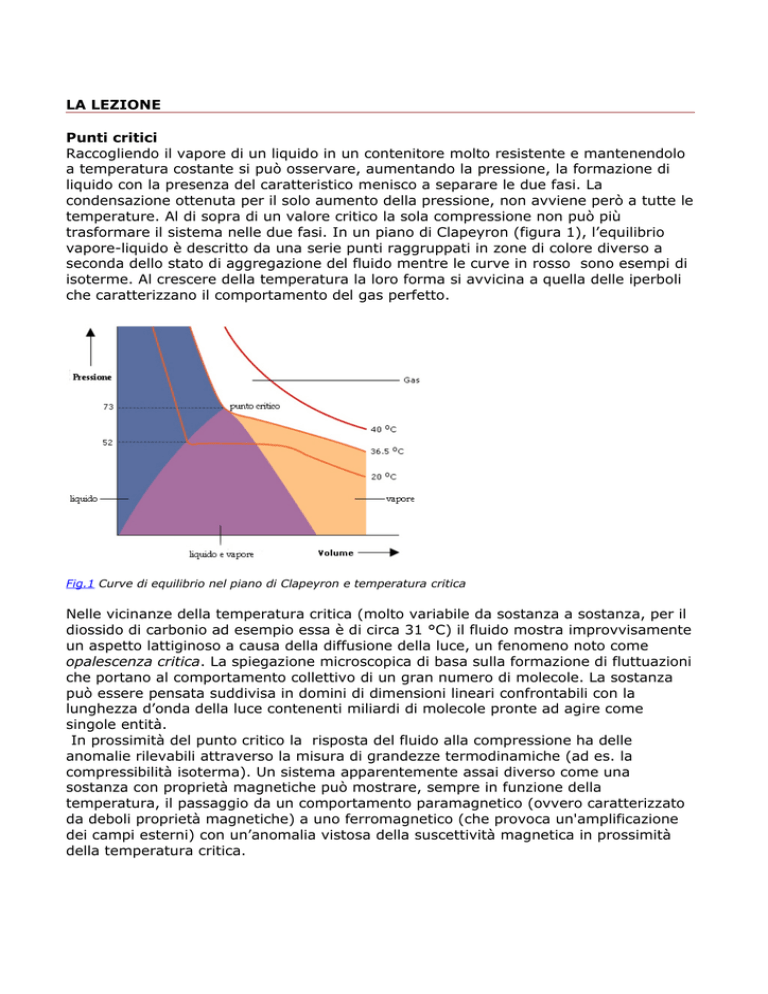
trasformare il sistema nelle due fasi. In un piano di Clapeyron (figura 1), l’equilibrio
vapore-liquido è descritto da una serie punti raggruppati in zone di colore diverso a
seconda dello stato di aggregazione del fluido mentre le curve in rosso sono esempi di
isoterme. Al crescere della temperatura la loro forma si avvicina a quella delle iperboli
che caratterizzano il comportamento del gas perfetto.
Fig.1 Curve di equilibrio nel piano di Clapeyron e temperatura critica
Nelle vicinanze della temperatura critica (molto variabile da sostanza a sostanza, per il
diossido di carbonio ad esempio essa è di circa 31 °C) il fluido mostra improvvisamente
un aspetto lattiginoso a causa della diffusione della luce, un fenomeno noto come
opalescenza critica. La spiegazione microscopica di basa sulla formazione di fluttuazioni
che portano al comportamento collettivo di un gran numero di molecole. La sostanza
può essere pensata suddivisa in domini di dimensioni lineari confrontabili con la
lunghezza d’onda della luce contenenti miliardi di molecole pronte ad agire come
singole entità.
In prossimità del punto critico la risposta del fluido alla compressione ha delle
anomalie rilevabili attraverso la misura di grandezze termodinamiche (ad es. la
compressibilità isoterma). Un sistema apparentemente assai diverso come una
sostanza con proprietà magnetiche può mostrare, sempre in funzione della
temperatura, il passaggio da un comportamento paramagnetico (ovvero caratterizzato
da deboli proprietà magnetiche) a uno ferromagnetico (che provoca un'amplificazione
dei campi esterni) con un’anomalia vistosa della suscettività magnetica in prossimità
della temperatura critica.
Fig 2 Domini magnetici
L’emergere sul piano macroscopico di proprietà caratteristiche del livello microscopico
è estremamente vistoso alle basse temperature. Con l’elio liquido si osservano
fenomeni di superfluidità in cui l’elio scorre attraverso forellini microscopici
apparentemente senza attrito o si muove, in alcuni tratti, nel verso opposto rispetto a
quello determinato dalla sola gravità.
fig 3 Proprietà dell’elio superfluido
fig 4 Transizione lambda nell’elio superfluido
Il calore specifico dell’elio 4 in prossimità del punto critico mostra un’anomalia e lo
studio del suo andamento in funzione dalla temperatura porta a una curva famosa che
per la sua forma è spesso associata alla lettera lambda. Altre transizioni di fase 1 assai
vistose sono quelle tipiche dei superconduttori in cui le sostanze (metalli a temperature
di pochi kelvin oppure “composti ceramici” a temperature di decine o centinaia di
kelvin) mostrano valori della resistività pressoché nulli evidenziando comportamenti di
levitazione in prossimità di magneti permanenti (il cosiddetto effetto Meissner dovuto
all’espulsione del campo magnetico all’interno del superconduttore). Nelle transizioni di
fase (del secondo ordine) descritte il materiale si comporta come un tutto e gli attriti o
le resistenze scompaiono facendo emergere su scale macroscopiche proprietà
tipicamente microscopiche.2
Alcune tappe della criogenia
Alla fine dell’Ottocento, si realizzano notevoli miglioramenti delle tecniche criogeniche
(compressori, tecnologia del vuoto, tubi capillari, termometri a resistenza, thermos,
apparati in cascata) capaci di portare alla liquefazione dell’idrogeno ( realizzata da
1
I passaggi di stato sono classificati come transizioni di fase del primo ordine, mentre queste sono dette
transizioni del secondo ordine. Nei passaggi di stato la funzione di stato (energia interna o entropia)
mostra una discontinuità mentre in quelle del secondo ordine la discontinuità è legata ad altre grandezze
termodinamiche derivabili dall’energia.
2
L’interpretazione teorica dei fenomeni critici delle transizioni di fase del secondo ordine non a caso è
avvenuta a partire dagli anni settanta utilizzando tecniche proprie della fisica delle particelle formando
quella che è detta teoria del gruppo di rinormalizzazione.
James Dewar della Royal Institute di Londra nel 1898) alla liquefazione dell’elio nel
laboratorio di fisica dell’Università di Leida di Heike Kamerlingh Onnes nel 1908 e infine
alla scoperta, nello stesso laboratorio, della superconduttività di alcuni metalli nel
1911.
fig 5 Superconduttività dei metalli
Nel 1912 Walther Hermann Nernst elabora una nuova versione del suo teorema del
calore con l’enunciato è impossibile realizzare una macchina termica capace di
raffreddare una sostanza sino alla temperatura dello zero assoluto. La strada verso lo
zero assoluto, il limite irraggiungibile secondo la versione di Nernst del terzo principio,
per molti anni si ferma nello studio dell’isotopo dell’elio più presente in natura (l’elio 4).
Alla temperatura di 2,1768 l’elio3 mostra il fenomeno della superfluidità (il valore della
viscosità crolla verso il valore zero4) con proprietà macroscopiche assai singolari come
l’effetto fontana realizzato da John F. Allen e Harry Jones nel 1938. I due fisici
utilizzano un bulbo riempito di polvere aperto sul fondo (dove pesca all’interno dell’elio
liquido) e con una piccola apertura nell’altra estremità. Riscaldando la polvere,
illuminandola, si provoca un flusso dell’elio liquido opposto al flusso di calore creando
una sorta di piccola fontana zampillante di elio liquido (figura 6).
fig 6 Effetto fontana nell’elio superfluido
Nel 1947 Samuel Cornette Collins del MIT realizza un liquefattore standard per l’elio,
ma solo nel 1972 i laboratori criogenici scoprono la superfluidità dell’isotopo dell’elio di
massa atomica 3 a temperature inferiori a 0,002 K, facendo un salto di tre ordini di
grandezza rispetto alla transizione lambda dell’elio 4. Dal 2000, grazie ai due isotopi
dell’elio e allo studio delle proprietà termodinamiche, sono adottati riferimenti standard
per le temperature che vanno da 0,0009 K a 5 K, secondo la tabella frutto del lavoro
internazionale di metrologia PLTS 2000 (Provisional Low Temperature Scale).
3
4
In natura la temperatura più bassa è 2,725 K, associata alla radiazione cosmica di fondo.
Le difficoltà di interpretazione dei fenomeni negli trenta era dovuta alla presenza nella transizione di due
tipi di liquido uno superfluido e l’altro con viscosità normale.
Fenomeni fisici di
Intervallo di
riferimento
temperatura (K)
Relazione pressione di
0,0009 a 1
fusione-temperatura per
l’elio 3 (relazione analitica)
Relazione pressione di
0,65 a 3,2
vapore-temperatura per
l’elio-3 (relazione analitica)
Relazione pressione di
1,25 a 2,1768
vapore-temperatura per
l’elio-4 sotto il suo punto
lambda (relazione
analitica)
Relazione pressione di
2,1768 a 5,0
vapore-temperatura per
l’elio-4 sopra il suo punto
lambda (relazione
analitica)
Ma cosa si conosce oggi per temperature inferiori a quelle caratteristiche dei due
isotopi dell’elio?
La teoria delle transizioni di fase del secondo ordine già nel 1982 ha dapprima
permesso di valutare la temperatura critica dell’antiferromagnetismo dei nuclei di rame
a 60 nK. In seguito con tecniche di raffreddamento laser, iniziate negli anni novanta, si
sono realizzati gas ultrafreddi a temperature via via decrescenti fino a raggiungere
valori inferiori a 1 nK (Wolgang Ketterle del MIT nel 2003).
A tali temperature il gas mostra le sue caratteristiche quantistiche (condensazione di
Bose Einstein) con un comportamento coerente che soddisfa l’altro enunciato del terzo
principio della termodinamica riconducibile a Planck: in prossimità dello zero assoluto
l’entropia del sistema tende a zero.
Il gas di Bose Einstein
In termodinamica il gas ideale è per certi versi l’equivalente del punto materiale o del
corpo rigido per la meccanica. È troppo difficile descrivere in modo esatto le variazioni
di pressione, temperatura e volume di un gas reale e cerco di approssimare il
comportamento di qualsiasi gas con un’equazione valida nel limite delle basse densità.
Cosa succede allora quando il gas non è più rarefatto ad esempio nel dominio delle
basse temperature? Il modello microscopico-statistico può essere utile sia per rendere
una nuova equazione più vicina al comportamento reale di gas. Non solo. Assumendo
valida per l’entropia del gas alle basse temperature il valore zero proposto da Planck si
pone il problema di dedurre statisticamente un’equazione per l’entropia dei gas ideali
valida in ogni intervallo di temperatura. Per effettuare questo tipo di calcolo si deve
decidere se le particelle siano distinguibili o indistinguibili. Negli anni ’20 dapprima
Fermi e poi Dirac esplicitano la statistica quantistica delle particelle di gas distinguibili,
mentre Bose e Einstein indipendentemente tracciano la statistica di quelle
indistinguibili. Oggi sappiamo che tutte le particelle sono bosoni o fermioni e le due
statistiche hanno pari dignità. Inoltre, sperimentalmente è possibile studiare gas di
atomi a temperature ultrabasse per verificare l’andamento verso lo zero previsto dal
terzo principio della termodinamica e da entrambe le statistiche quantistiche dei gas
ideali. Nel 1995 Eric A. Cornell, Carl E. Wieman al Joint Institute for Laboratory
Astrophysics di Boulder e Wolfgang Metterle al Massachusetts Institute of Technology
realizzano campioni di gas monoatomico di atomi di sodio ad alta densità e ultrafreddi
impiegando il raffreddamento laser e trappole magnetiche.
fig 7 Raffreddamento laser
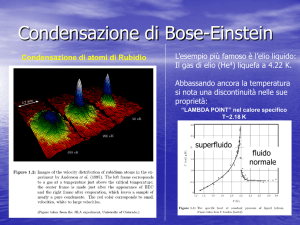
fig 8 lezione Condensazione di Bose Einstein
Il gas a temperature bassissime mostra una transizione di fase, detta condensazione di
Bose Einstein, in cui una frazione considerevole degli atomi del gas si avvicina allo
stato ad entropia zero. La spiegazione del fenomeno è riconducibile al dualismo onda
corpuscolo. Dalle considerazioni di de Broglie degli anni venti la lunghezza d’onda
caratteristica del pacchetto d’onda di una particella avente quantità di moto mv è data
dall’espressione ldB=h/mv. Intorno a un valore della temperatura prossimo alla
temperatura critica le densità degli atomi diventano così elevate che tale lunghezza è
confrontabile con la distanza media tra due particelle e i pacchetti d’onda iniziano a
sovrapporsi. Un numero consistente di atomi si accumula nello stato di energia più
basso (le particelle sono indistinguibili e “condensano” tutte nello stesso stato).
Teoricamente abbassando ulteriormente la temperatura esse raggiungono lo stesso
stato con una unica onda di materia caratteristica di tutto l’insieme statistico,
caratterizzato da S=0 in accordo all’equazione S=k lnW con W=1. Nell’impossibilità
pratica di giungere allo zero assoluto solo una percentuale macroscopica di gas subisce
la condensazione caratteristica delle particelle indistinguibili descritta dalla statistica di
Bose Einstein.