gain-guide laser

Capitolo 2
LASER
PROBLEMA DEL CONFINAMENTO
Abbiamo visto la duplice natura del confinamento: fotonico ed elettronico, entrambi
suddivisi in confinamento verticale ed orizzontale.
La doppia eterostruttura garantisce sia il confinamento elettronico di tipo verticale, in quanto
essa impedisce la diffusione dei portatori nei cladding, che quello ottico, sempre di tipo verticale,
grazie alla differenza degli indici di rifrazione.
La classificazione dei laser, che coinvolge problemi di tecnologie e di costi, riguarda il
confinamento ottico ed elettronico di tipo orizzontale.
I laser vengono suddivisi in:
 GAIN-GUIDE: non ha nessuna cura nel realizzare confinamento ottico laterale, ma compie
sforzi per realizzare quello elettrico tramite differenze di drogaggi.
 QUASI-INDEX-GUIDE relizza un buon confinamento ottico ed elettronico, il primo grazie
alla modulazione dell’indice di rifrazione di guida, e il secondo tramite l’indroduzione del
CAP.
 STRONGLY-INDEX-GUIDED: realizza un ottimo confinamento, sia ottico che elettrico,
grazie alla guida sepolta e la CAP.
corrente
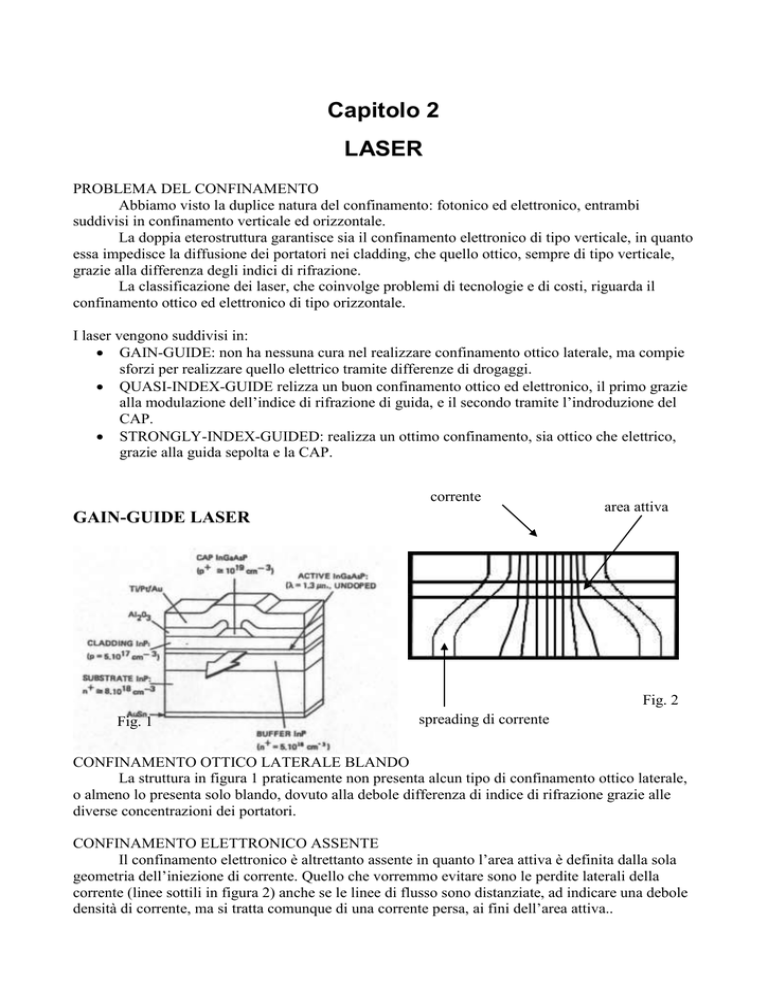
GAIN-GUIDE LASER
area attiva
Fig. 2
Fig. 1
spreading di corrente
CONFINAMENTO OTTICO LATERALE BLANDO
La struttura in figura 1 praticamente non presenta alcun tipo di confinamento ottico laterale,
Fig. 2
o almeno lo presenta solo blando, dovuto alla debole differenza di indice di rifrazione grazie alle
diverse concentrazioni dei portatori.
CONFINAMENTO ELETTRONICO ASSENTE
Il confinamento elettronico è altrettanto assente in quanto l’area attiva è definita dalla sola
geometria dell’iniezione di corrente. Quello che vorremmo evitare sono le perdite laterali della
corrente (linee sottili in figura 2) anche se le linee di flusso sono distanziate, ad indicare una debole
densità di corrente, ma si tratta comunque di una corrente persa, ai fini dell’area attiva..
TECNICHE DI CONFINAMENTO ELETTRICO:
Si tratta di tecniche non particolarmente raffinate: un’impiantazione nel caso della prima
soluzione e una diffusione nel caso della seconda, ma che consentono di confinare quanta più
corrente possibile all’interno dell’area attiva evitando le perdite laterali.
1° SOLUZIONE
Una prima strategia è quella di
definire delle zone altoresistive tramite
impiantazione che non deve
coinvolgere l’area attiva. Si chiama
SCHELL OF IMPLANT cioè
impiantazione superficiale che tende a
rendere intrinseco il semiconduttore
intorno all’area attiva. Queste zone
tendono quindi a concentrare tutta
l’intensità di corrente nell’area attiva,
dato che le zone circostanti presentano
una maggior resistenza.
Fig. 3
2° SOLUZIONE
Questa seconda strategia è
praticamente la duale della precedente.
Presenta un ulteriore strato, che si chiamo
CAP. Si tratta di uno strato di
semiconduttore quaternario (dato che lo è
lo strato attivo) a basso gap drogato di
tipo n. D’ora in poi questo strato sarà
praticamente sempre presente. E’
necessario che sia a basso gap in quanto
in questo modo la giunzione metallo
Fig. 4
semiconduttore, che costituisce un diodo
schottky, ha una bassa tensione di soglia,
a causa della bassa barriera. Per confinare
meglio la corrente inoltre, facciamo una diffusione di tipo p+ che interessa tutto il CAP e parte del
claddding: è necessario farla p perché vogliamo costruire un canale di collegamento tra il cladding e
la metal, e lo droghiamo pesantemente (+) per diminuire il più possibile la resistenza di contatto. La
zona n sarebbe il catodo di un diodo e quindi la giunzione p-n risulterebbe polarizzata inversamente,
cosa che comporta il confinamento della corrente nell’area attiva eliminandone gli spreading.
Una soluzione di questo tipo è migliore della prima, perché oltre ad un peggior
confinamento elettrico nella prima soluzione è presente un gran numero di difetti a causa
dell’impiantazione ionica..
MISURE DI FAR-FIELD
Il Gain-guide resta comunque un oggetto
“da battaglia”, in quanto la sua area attiva ha
dimensioni rettangolari, per una questione di tecnologie:
area attiva
0.4 m
lo spessore dell’area attiva può essere fatto piccolo a
piacere in quanto formato per epitassia; la dimensione laterale è determinata dalla risoluzione
2 m più
litografica della geometria planare. La larghezza della zona che emette è quindi comunque
grande dello spessore. Questo comporta una perdita di coerenza spaziale
E
intensità di
campo
elettrico
2
1
1
2

Anziché avere uno spot circolare ho un’emissione di tipo ellittica, con la conseguente necessità di
rifocalizzare il mio sistema.
Questo tipo di radiazione non è dovuto soltanto a motivi geometrici ma se interpretiamo il
sistema come una guida dielettrica, vediamo che per una polarizzazione verticale (2) la guida può
ammettere un solo modo di propagazione, mentre per una polarizzazione orizzontale (1) il sistema
potrebbe ammetterne più d’uno:
1
2
STRONGLY INDEX GUIDED
Fig. 5
Questa struttura, molto
importante, detta BRS
Struttura a Ridge (guida)
Sepolta, è caratterizzata dal
fatto che il cladding di tipo p e
quello di tipo n di toccano, ed
hanno in mezzo una struttura
costruita di materiale diverso:
l’area attiva costituita da un
materiale quaternario,
completamente affogato nel
materiale binario.
PROCESSO TECNOLOGICO per realizzare il BRS:
E’ necessario crescere per epitassia uno strato quaternario uniforme, realizzare un attacco selettivo
anisotropo, in modo da lasciare le pareti dell’area attiva verticali, depositare quindi per epitassia il
cladding p in modo riplanarizzante tale da smussare gli angoli.
OTTMO CONFINAMENTO OTTICO
La differenza strutturale dello strongly index guided è costiruita dal fatto che l’area attiva è
concepita come una guida effettiva, non blanda, dato che essendo fatta con un materiale diverso
realizza un ottimo confinamento ottico. Il che significa che anche in senso laterale ho una netta
differenza tra gli indici di rifrazione.
BUON CONFINAMENTO ELETTRICO
Potremmo essere portati a pensare che il drogaggio di tipo p+ del CAP comporti una netta
perdita di confinamento elettrico e causa dell’allargamento della corrente. Al contrario, questa
struttura realizza anche un buon confinamento elettrico, anche se una certa dispersione della
corrente è comunque presente.
Ma perché il confinamento elettrico è comunque buono? Perché il quaternario dell’area
attiva conduce meglio del binario che lo circonda. Se pensiamo di rappresentare la struttura con uno
schema elettrico troviamo la seguente situazione:
La struttura può essere rappresentata come il parallelo
di tre diodi, dei quali quello al centro ha una V minore
rispetto agli altri due in quanto è fatto con un materiale a gap
minore. In condizioni di bassa iniezione conduce solo il
diodo centrale, a causa della sua bassa V, mentre gli altri
due hanno una tensione applicata insufficiente ad accenderli.
Le correnti di perdita, quindi, intervengono soltanto in
condizioni di alta iniezione quando cominciano a condurre
gli altri due diodi.
Per bassi livelli di iniezione quindi, si riesce a garantire un buon confinamento elettronico, mentre
ad alte iniezioni, il confinamento è minore.
Fig. 6
Questa struttura, detta
MUSHROOM (a causa della sua
struttura a fungo) è costituita da uno
strato superiore (la cappella del
fungo) di n-cladding, al di sotto si
trova l’area attiva di quaternario e
tutto attorno c’è uno strato di
dielettrico. E’ importante sottolineare
che a differenza delle altre strutture,
l’n-cladding sta sopra!
PROCESSO TECNOLOGICO per realizzare il MUSHROOM
Si tratta di un processo molto più complicato di quello necessario per realizzare il BRS, e
quindi molto più costoso. In pratica infatti viene usato pochissimo, si tratta piuttosto di una struttura
da portare in congresso, per mostrare le nostre capacità tecnologiche.
Si realizza il cladding di tipo n, binario, poi si cresce il
n-clad
quaternario dell’area attiva, quindi il cladding di tipo p. A
questo punto arrivati ad una situazione del genere in figura 7
p-clad
è necessario erodere lo strato dell’area attiva. Questo è
possibile solo immergendo la struttura in un attacco acido
SUB
selettivo che eroda solo il quaternario e non il binario.
Fig. 7
Questo agente chimico deve essere in grado di penetrare
n-clad
anche negli interstizi, consumando il quaternario. Si
raggiunge in questo modo la struttura in figura 8.
p-clad
Il problema è definire per bene la geometria dell’area
attiva, in quanto in un processo di attacco umido non si
riuscirà mai ad avere, ad esempio delle superfici laterali
Fig. 8
SUB
perfettamente verticali, anche perché stiamo parlando di
un’area attiva della larghezza del m.
A questo punto tutta la struttura deve essere posta in un ambiente reattivo che deposita
dappertutto il dielettrico.
Data la difficoltà di processo la resa tecnologica di questo procedimento è molto bassa, può
darsi che si riesca a costruirne correttamente uno su dieci
Attenzione alla polarizzazione dato che l’n sta sopra,; questo è dovuto a motivi tecnologici,
in quanto “forse” è più facile attaccare con l’acido il Fosfuro di Indio drogato n piuttosto che quello
drogato p.
CONFINAMENTO ELETTRICO TOTALE
Questo è il grosso vantaggio della struttura Mushroom, in quanto realizza un confinamento
elettrico ben superiore al BRS, dato che a causa del dielettrico, la corrente non può far altro che
passare tutta dalla zona attiva, il che comporta un confinamento elettronico totale.
Le applicazioni di questa struttura sono principalmente quelle che riguardano la
modulazione analogica.
CARATTERISTICHE PORENZA-CORRENTE
A parità di fattori elettrici, fattori fisici ed ottici.
P
Saturazione
MSH
Po
BRS
Il Mushroom segue bene la
curva ideale lineare dato che in
questa struttura tutta la corrente
passa dalla zona attiva.
Mentre il BRS si discosta
dalla linearità, ma satura agli
stessi livelli. Il che significa che
per alte iniezioni il BRS per
ottenere la stessa potenza ottica
Po deve sobbarcarsi anche la
corrente di perdita I (corrente di
“leackage”).
I
I
I
La saturazione del materiale è dovuta ad alti livelli di iniezione. Aumentando ulteriormente le
corrente, la potenza fornita viene convertita in calore, mentre le potenza ottica non aumenta più.
La spesa di tecnologia dovuta al mushroom, quindi non è altro che la ricerca di eliminare
questa perdita di linearità, per un range di correnti il più ampio possibile.
Per modulazioni digitali è infatti tollerabile questa perdita di linearità, ma così non è per le
modulazioni analogiche nelle quali comporterebbe una distorsione del segnale.
Il MUSHROOM ed il BRS costituiscono due esempi caratteristici, di strutture fortemente
guidate a indice, in cui è esplicito il confinamento ottico laterale. Si tratta infatti di effettive guide
dielettriche in quanto un materiale ad alto indice di rifrazione è confinato, anche lateralmente, e
non solo superiormente ed inferiormente da un materiale ad indice di rifrazione minore.
La struttura a BRS è quella che va per la maggiore, non solo per i laser ma anche per gli
amplificatori ottici.
Il vantaggio di avere un laser all’interno della guida dielettrica si ripercuote essenzialmente
sulla coerenza di tipo spaziale
PARENTESI:
GUIDA DIELETTRICA
La propagazione della luce può
avvenire nella guida solo se l’angolo di

congruenza
 critico
Ma non tutti gli angoli sono permessi, ne
n1
esiste un lotto discreto: è sempre permesso
= 0 e via dicendo…
Ad ogni valore di  corrisponde un modo di
n2
propagazione.
Innescando un certo numero di fotoni all’inizio della fibra essi la attraverseranno con modi di
propagazione diversi (possiamo immaginarli su dei tapis-roulants) e con conseguenti velocità
diverse, dovute soprattutto alla diversità del cammino percorso.
Della velocità del fotone mi interessa solo la proiezione lungo l’asse longitudinale, che
schematizzo come velocità intrinseca del modo di propagazione.
Supponiamo che il fotone sia rappresentato con l’onda:
A0 cos(t-kx)
Dove k è il fattore di propagazione spaziale
k= 2/= 2n/c= k0n
Ogni modo ha il suo vettore d’onda.
n2
Supponiamo che quello al centro viaggi alla velocità della luce (ma come vedremo così non è):
il modo fondamentale avrà vettore d’onda:
k1=n1k0
il modo superiore associato a i :
kin1k0
(1)
Poniamo
ki= ngk0 n1k0
Dobbiamo fare un passaggio mentale che prevede di immaginare che la luce che viaggia in un certo
modo superiore associato all’angolo i si propaghi in un altro mezzo, fittizio, con indice di
rifrazione ng detto indice di rifrazione di guida (ce n’è uno per ogni i, e non esiste veramente, è
solo una posizione ingegneristica).
Sappiamo che un modo di propagazione superiore può istaurarsi in una guida solo se la
frequenza di lavoro è al di sopra della frequenza di taglio del modo, quindi se riusciamo a fare sì
che la frequenza di taglio del primo modo superiore sia mantenuta al di sopra della nostra frequenza
di lavoro, essa impedisce la propagazione del primo modo ed a maggior ragione di tutti gli altri.
Così si riesce a realizzare una guida monomodale.
Ma da cosa dipende la frequenza di taglio dei modi superiori?
Dipende dalle stesse cose da cui dipendeva il fattore di confinamento: dalle dimensioni geometriche
della guida e dalla differenza tra gli indici di rifrazione dei due mezzi. Per realizzare guide
monomodali è necessario fare delle guide strette, così i fotoni devono incanalarsi in un unico modo
di propagazione.
Quanto detto vale anche per i laser, in modo tale che i fotoni che nascono diano luogo,
all’uscita, un solo lobo centrale, e non due.
Supponiamo quindi di aver realizzato un laser che ha all’interno una guida modomodale, in
cui è ammesso il solo modo di propagazione fondamentale. Le relazioni (1) valgono ancora perché
il fattore di propagazione assiale di questo modo non coincide con n1k0 perché non siamo in uno
spazio libero, con coefficiente di rifrazione n1,ma siamo in una guida limitata. La potenza
elettromagnetica coinvolge, come abbiamo detto a suo tempo a proposito del fattore di
confinamento, sia il core che i cladding, quindi il modo di propagazione assiale, in funzione sia
della larghezza della guida che della differenza degli indici di rifrazione, possiede un indice di
rifrazione di guida intermedio, minore di quello che si avrebbe nello spazio libero.
Di fatto, posso variare l’indice di rifrazione di guida ng del modo fondamentale, unico che si
può instaurare, variando lo spessore della guida o la differenza tra n1 ed n2 , senza dover cambiare
effettivamente materiale. In questo modo quindi riesco ad esaltare la differenza tra gli indici di
rifrazione n g 1 ed n g 2 di guida (non quelli effettivi, che mi permettono di far finta che la luce si stia
propagando il un mezzo illimitato, ma di fatto sono minori di quelli effettivi).
A questo punto abbiamo le basi per comprendere la strategia della situazione intermedia.
QUASI-INDEX-GUIDE
Il quasi sta ad indicare che, in termini di confinamento ottico laterale, non c’è un materiale
diverso per realizzarlo, come abbiamo visto nelle due strutture dello STRONGLY INDEX
GUIDED, ma non si lascia nemmeno che il confinamento ottico laterale sia blando come nel GAIN
GUIDED, dovuto solo alla debole differenza di indice di rifrazione a causa della differenza di
concentrazione dei portatori.
x
Fig. 9
La struttura più semplice
da realizzare è il RIB
(fossato”forse) in figura 9, nel
quale modulando lo spessore del
core, facciamo in modo che lo
spessore dell’area attiva sia
maggiore del resto del core. In
questo modo, per quanto sopra
detto, nel verso longitudinale (in
figura la direzione x) abbiamo
ottenuto una modulazione
dell’indice di rifrazione di guida
(vedi fig 10)
PROCESSO TECNOLOGICO per realizzare il RIB
Una volta deposto per epitassia l’ n cladding tramite litografia vi si ricava in esso un fossato.
Tramite poi una crescita epitassiale perfettamente ripianante ottengo un core più spesso al centro e
più sottile ai lati.. Nota: è importante che la crescita sia perfettamente ripianante, altrimenti non
funziona più nulla.
p-cl
Fig.10
area attiva
BUON CONFINAMENTO
OTTICO
n-cl
In questo modo, grazie
alla differenza di indice di
rifrazione si riesce a realizzare un
buon confinamento ottico, sempre
meglio del Gain guided, ma non
perfetto come nello Strongly
index guided.
x
ng
ng1
ng1
ng2
x
Completamente diverse sono le struttura a RIDGE.
Vediamo prima il
RIDGE RWL.
z
x
y
Fig. 11
Sia cladding n e p
che l’area attiva sono
fatti con il
quaternario
InGaAsP,
rispettivamente di
=1.1m (quindi
gap=1.13eV) e
=1.3m (quindi
gap=0.95eV) il che
significa che questa
struttura è adatta a
lavorare in seconda
finestra. Il buffer e il
substrato sono di
binario InP.
CONFINAMENTO OTTICO
Qui il cladding di tipo p, lo strato attivo e il cladding di tipo n sono molto sottili, e quindi
praticamente attaccati alla superficie.
Osserviamo in figura 12 l’andamento degli indici di rifrazione effettivi dei materiali lungo le due
diverse direzioni: x e y:
n
Dielettrico
Fig. 12
n
pclad
area nattiva clad
buffer
x
buffer p
pclad
area nattiva clad
buffer n
y
Ai lati dell’area attiva, quindi lungo la direzione x, il materiale che c’è prima dello 0, ovvero
subito prima del p-cladding è dielettrico, quindi con un indice di rifrazione infimo. Dato che l’area
attiva si ritrova alle spalle un indice di rifrazione tanto basso, l’indice di rifrazione di guida, in
questa zona, sarà basso.
Nella parte centrale, quindi lungo la direzione y, invece, si ha una ricrescita molto spessa,
che serve anche da incanalamento della corrente, di binario InP drogato p; qui l’andamento
dell’indice di rifrazione effettivo diventa simmetrico. Di fatto cambiando la differenza di indice di
rifrazione abbiamo cambiato il modo guidante, ovvero l’indice di rifrazione di guida che qui al
centro risulta essere maggiore.
La strategia di confinamento ottico qui, non è quella di
ng
cambiare la geometria della struttura, ma cambiare soltanto
Fig. 13
l’indice di rifrazione di guida, agendo sulla differenza dei gap
invece che sullo spessore della guida stessa. La situazione in
termini di indice di rifrazione di guida che ritroviamo lungo
l’asse z riportato in figura 11 è quello di figura 13.
CONFINAMENTO ELETTRICO
Da notare che le strutture a RIDGE realizzano anche un ottimo
z
confinamento elettrico in quanto tutta la corrente viene ad essere
convogliata a passare nel CAP. La funzione del CAP, immancabilmente presente, è tutta di tipo
ohmico, e non è solamente quella di diminuire la resistenza di contatto (diodo schottky), ma anche
quella di migliorare il contatto ohmico sul fosfuro di indio. Infatti la deposizione della metal su InP
drogato p comporta dei buoni contatti ohmici in certi punti, ma peggiori in altri; questo
comporterebbe una densità di corrente completamente sbilanciata sulla superficie. La funzione del
CAP p+, tanto fortemente drogato da essere equiparato ad un metallo, contribuisce ad uniformare la
caduta di potenziale, e quindi lo spreading di corrente al di sopra dell’area attiva, in modo tale che
la densità di corrente risulta uniformemente distribuita in essa.
La struttura a RIDGE
OVERGROWN di figura 14 è
praticamente identica alla precedente ma
presenta difficoltà tecnologiche maggiori.
Fig. 14