La misura della temperatura Note introduttive

La misura della temperatura
Note introduttive
Al contrario di altre grandezze fisiche,
l’interesse per la definizione e la misura
della temperatura compare molto tardi nella
storia dell’umanità.
Le ragioni di tale
singolarità sono due:
•La temperatura non ebbe importanza
economica fino al XIX secolo (ovvero fino
all’avvento
all
avvento della rivoluzione industriale e
delle macchine termiche);
• La temperatura è una grandezza di tipo
intensivo
te s o (è necessario
ecessa o ricorrere
co e e a
alla
a
misura di qualche grandezza che dipenda in
modo riproducibile dalla temperatura).
La misura della temperatura
Note introduttive
Wikipedia®
In fisica,, ed in p
particolare in termodinamica,, le
proprietà intensive sono quelle proprietà che non
dipendono
dalla
quantità
di
materia
o
dalle
dimensioni del campione ma soltanto dalla natura e
dalle condizioni nelle quali si trova. Al contrario una
proprietà si dice estensiva se dipende dalle
dimensioni del sistema.
sistema
La temperatura e la pressione sono esempi di
grandezze intensive; viceversa volume, entalpia ed
entropia
t i sono grandezze
d
estensive.
t
i
I f tti se, ad
Infatti
d
esempio, il sistema in esame è costituito dall'acqua
in un contenitore, rimuovere acqua varia il volume
(estensivo) ma non la temperatura (intensiva).
2
La misura della temperatura
Note introduttive
•Al contrario delle altre grandezze, tipo massa,
tempo, lunghezza, non è possibile misurare
temperatura per confronto con campioni di
temperatura.
•E’ quindi necessario definire
una
metodologia che consenta di misurare con
estrema accuratezza la temperatura
p
e che
possa essere considerata di riferimento.
La misura della temperatura
La scala termometrica
•Nasce
quindi
il
concetto
di
scala
termometrica definendo la temperatura come
grandezza strumentale. E’ necessario in
questo caso:
9Scegliere una sostanza e una
termometrica;
proprietà
9Definire la natura della scala (lineare o
meno);
9Scegliere i punti fissi (attribuire dei valori a
degli
stati
termici
ben
definiti
e
riproducibili).
9Definire,
sulla
base
delle
proprietà
termometriche, le funzioni di interpolazione
tra i vari punti fissi.
La misura della temperatura
La scala termometrica
Le prime scale di temperatura
introdotte
furono
la
Scala
Fahrenheit e la Scala Celsius.
Celsius
•Utilizzano come sostanza termometrica
il mercurio e come proprietà la
dil t i
dilatazione;
•Utilizzano due punti fissi. Punto di
solidificazione dell’acqua (32°F, 0°C) e
punto di ebollizione dell’acqua (212°F,
(212°F
100°C);
•Suppongono che la dilatazione del
mercurio
i con la
l temperatura
t
t
sia
i lineare
li
.
Si passa da una scala all’altra
utilizzando la relazione:
T(°C)=5/9(t(°F)-32)
La misura della temperatura
La scala termometrica
Le scale di temperatura definite con
questi criteri hanno un certo criterio di
arbitrarietà
bit i tà nella
ll scelta
lt della
d ll sostanza,
t
della proprietà e della relazione tra tale
proprietà e la temperatura.
Ad es. chi ci assicura che a parità di
variazione di temperatura, DT, in due
punti
ti della
d ll scala
l non sii abbiano
bbi
d
due
dilatazioni diverse?
… e se il materiale varia leggermente,
come varia la relazione tra temperatura
e dilatazione?
Ciò comporta l’inconveniente di poter
costruire un numero illimitato di scale
empiriche
che
danno
misure
in
disaccordo.
La misura della temperatura
La scala termodinamica assoluta
Una scala ideale di temperatura
p
dovrebbe
prescindere
da
ogni
riferimento alla sostanza adottata e alla
natura della proprietà utilizzata per
misurare la temperatura.
E possibile realizzare una tale scala
E’
ricorrendo
alle
leggi
della
termodinamica.
Si ottiene così la scala termodinamica
o assoluta.
La misura della temperatura
La scala termodinamica assoluta
La scala termodinamica (1854) fa
riferimento al Ciclo di Carnot. Per esso si
ha:
Q1/Q0=T1/T0
Q0, T0
Q1, T1
Tale relazione p
permette di ottenere lo stato
termico di un sistema da misure di tipo
calorimetrico.
IInfatti
f tti fissato
fi t un punto
t fisso
fi
(
(punto
t triplo
ti l
dell’acqua, T0=273,16K) rimane un legame
tra T1 e i il calore scambiato.
La misura della temperatura
La scala termodinamica assoluta
La scala termodinamica basata sul
ciclo di Carnot è ideale e quindi
non realizzabile.
Fortunatamente si è visto che utilizzando
un altro principio fisico, la legge dei gas
perfetti ed utilizzando lo stesso punto fisso
(punto triplo dell’acqua, T0=273,16K), è
possibile
produrre
una
scala
termometrica equivalente a quella
termodinamica assoluta.
La misura della temperatura
La termometria a gas
La termometria a gas utilizza la legge dei
gas perfetti pere realizzare un termometro:
PV=nRT
n sono le moli del gas;
R è la costante universale dei gas
E’ possibile realizzare termometri a:
volume
o u e cos
costante:
a e: P/P
/ 0=T/T
/ 0
pressione costante: V/V0=T/T0
Scelto un valore di
temperatura e quindi di
pressione di riferimento
(temperatura del punto
triplo dell
dell’acqua)
acqua) si ha:
T=273.16 P/Po
NB: A causa di non idealità è necessario introdurre dei
termini correttivi e la formula diventa:
PV=nRT(1+nB/V+n2C/V2+…)
10
Termometro a gas
P
P0
•Si immerge il bulbo di gas nel bagno di cui si vuole misurare la
temperatura;
•Si
Si alza
l o sii abbassa
bb
il serbatoio
b t i R in
i modo
d tale
t l che
h l’altezza
l’ lt
d l
del
mercurio nella colonna di sinistra sia sempre la stessa. In questo
modo si mantiene costante il volume occupato dal gas.
•Dalla differenza di altezza h del mercurio nei due bracci si misura
la pressione del gas:
•P0 = P + ρgh
•P = P0 - ρgh (P=pressione del gas)
•Si trova che vale la relazione: T = C·P
•C è una costante di proporzionalità che va determinata con una
procedura di calibrazione (punto di ebollizione).
11
La misura della temperatura
SIPT (ITS-90)
La
scala
termodinamica
assoluta
richiede delle apparecchiature molto
sofisticate che non tutti i laboratori hanno
a disposizione.
E’ stata adottata pertanto una scala
convenzionale che risponde ai seguenti
requisiti:
• E’ accettata da tutti;
•E’ più
pratica;
ti
facilmente
• E’ più precisa
riproducibilità;
traducibile
ed
ha
nella
maggiore
•Ricalca
la
scala
termodinamica
realizzata con il termometro a gas.
12
La misura della temperatura
SIPT
La VII Conferenza Generale dei Pesi e
delle Misure istituì nel 1927 la Scala
Internazionale
i
Pratica
i
dii Temperatura
(SIPT), definendo:
•Unità di misura;
•Intervalli operativi;
•Punti
P ti fissi;
fi i
•Equazioni interpolatrici, cioè relazioni
tra proprietà termiche e temperatura;
•Strumenti interpolanti (ovvero tipo di
termometro).
Nel tempo
p si sono avvicendate le SIPT27, SIPT-48, SIPT-68 (ritoccata nel ’75).
Attualmente è in vigore la ITS-90
13
La misura della temperatura
Le unità di misura della scala (ITS
(ITS-90)
90)
•L’ITS 90 accetta come unità di misura il
Kelvin ((K)) e il g
grado Celsius ((°C).
)
•Per le temperature espresse utilizzando
le due unità si utilizzano rispettivamente
i simboli T90 e t90.
•Fra le due espressioni sussiste ancora
la relazione:
t90 (°C) = T90 (K) –273.15
14
La misura della temperatura
Intervallo di applicabilità: (ITS-90)
(ITS 90)
•L’ITS 90 è definita a partire da
0 65K fino alle temperature più alte
0,65K
attualmente misurabili (utilizzando il
pirometro monocromatico).
•Essa presenta un ampliamento
dell’intervallo
dell
intervallo
di
temperature
misurabili (la SIPT-64 si fermava a
13.8 K).
•Esistono delle differenze tra i valori
di temperatura stimati con la ITS 90
e i corrispondenti valori stimati
utilizzando le scale precedenti.
15
La misura della temperatura
ITS-90:
ITS
90: Strumenti interpolanti
Vengono introdotti quattro intervalli principali (in
funzione degli strumenti utilizzati per la stima della
temperatura).
p
)
Per ogni intervallo vengono introdotti dei
sottointervalli, individuati da opportuni punti fissi.
Ogni sottointervallo è caratterizzato da una sua
legge interpolante.
•[0.65 K ÷ 5,0 K]
•Termometro a pressione di vapore di una
miscela di 3He e 4He;
•[3,0K ÷ 24.5561K]
•Termometro a volume costante ad elio;
•[13,8033K ÷ 961.78°C]
•Termometro a resistenza al platino;
•Sopra i 961.78°C
•Pirometro monocromatico.
16
La misura della temperatura
Utilizzando altri principi fisici è possibile
introdurre altri criteri per la misura della
temperatura. Si ottengono in la modo:
•La termometria magnetica;
La termometria acustica;
•La
•La termometria a rumore;
•La termometria a radiazione;
La misura della temperatura
La termometria magnetica
La termometria magnetica permette di
misurare la temperatura assoluta per valori
di temperatura molto bassi,
bassi dove non può
essere utilizzato il termometro a gas (meno
di 2 K).
Esso si basa sulla proprietà che ha la
suscettività magnetica (μ r = χ + 1) di alcuni
materiali di subire variazioni con la
temperatura, secondo la relazione:
c
χ=
T
IIn realtà
ltà sii ottiene
tti
cosìì una temperatura
t
t
magnetica T* che va successivamente
corretta.
Si riesce in tal modo,
modo ad arrivare a
temperature fino a 0,01K
18
La misura della temperatura
La termometria acustica
La termometria acustica
sfrutta la
dipendenza della velocità del suono in un
gas dalla
d ll temperatura
t
t
d l gas stesso
del
t
(
(per
misurare basse temperature).
Si ha infatti:
V02=γ0RT/M
Anche in questo caso sono necessarie
delle correzioni.
Si arriva con questa tecnica a misurare
temperature fino a 2K.
19
La misura della temperatura
La termometria a rumore
La
termometria
a
rumore
sfrutta
la
dipendenza
p
del rumore p
prodotto ad un
resistore dalla sua temperatura:
Veff2=4kTRΔf
Con k= 1,380622 10-23 J/K-1.
Questa tecnica, ancora in fase di sviluppo,
si
presenta
promettente
alle
alte
temperature.
temperature
20
La misura della temperatura
La termometria a resistenza
La termometria a resistenza
utilizza, per la
costruzione di sensori di temperatura il
fenomeno della dipendenza della resistività
dalla temperatura:
ρ(t)= ρ(t0)(1+αΔt+βΔt2+…) ≈ ρ(t0)(1+αΔt)
•Il Nickel è il più sensibile
ma poco lineare alle alte
temperature;
•Il Rame è lineare ma si
ossida facilmente e quindi si
deve usare alle basse temp;
•IlIl Platino offre il miglior
compromesso tra linearità,
stabilità e sensibilità.
La misura della temperatura
Schematizzazione di un sensore standard al
Platino per applicazioni da laboratorio
Range: [–200°C, 1000°C]
Accuracy: ±0.001°C
Primary Standard Platinum Resistance Thermometer, SPRT
La misura della temperatura
Schematizzazione di altri sensori al Platino
Range: [–200°C, 500°C]
Accuracy: ±0.03°C
α=0.00392 °C–1
Secondary Standard Platinum Resistance Thermometer, SPRT
Range: [–200°C, 500°C]
Accuracy: da ±0.25°C a ±2.5°C
Industrial Platinum Resistance Thermometer
La misura della temperatura
Sensori al Platino a film sottile
Range: [-50°C, 400°C]
Accuracy: da ± 0.5°C a ±2.0°C
α=0 00385°C
α=0.00385
C
La misura della temperatura
La termometria a resistenza
Dipendenza della resistività dalla temperatura:
Per i metalli (RTD) si ha:
ρ(t)=
( ) ρ(t
( 0)(1+αΔ
Δt+
+βΔt2+…)
+ ) ≈ ρ(t
( 0)(1+αΔ
Δt))
Ad esempio per il platino vale α=3.912x10-3 /K e
β=−6.179912x10-7 /K2 e ciò garantisce che fino a
temperature di circa 650°C il termine lineare e
10 volte più grande del termine quadratico.
Per i semiconduttori vale:
ρ (T ) = ρ (To ) e
E⎛ 1 1 ⎞
⎜⎜ − ⎟⎟
k ⎝ T To ⎠
Il coefficiente di temperatura - (Ω/Ω)/K è positivo per i sensori metallici,
negativo per i sensori a semiconduttore.
semiconduttore
La misura della temperatura
La termometria a resistenza: RTD
Per i metalli (RTD) si ha:
ρ(t)=
ρ(
) ρ(
ρ(t0)(
)(1+αΔt+βΔt
β 2+…)) ≈ ρ(
ρ(t0)(
)(1+αΔt))
L’aumento della resistività con la
temperatura
te
pe atu a è do
dovuto
uto a
all’aumento
au e to
dell’agitazione termica!!!!
ρl
R=
S
l
R ≈ ρ( t0 ) ( 1 + αΔt ) = R0 ( 1 + αΔt )
S
R = R0 ( 1 + x )
La misura della temperatura
Confronto tra i termometri a resistenza
Tra i metalli che si possono impiegare per la
costruzione dei termometri ricordiamo:
•Il p
platino ((es. PT100),
), utilizzato come campione,
p
,
è adatto a misure nell’intervallo –270°C, 1100°C;
E per applicazioni più economiche e meno
accurate:
•Il nickel, utilizzato nell’intervallo –100°C, 200°C;
•Il rame, utilizzabile nell’intervallo di temperatura
-150°C, 150°C.
La misura della temperatura
I termistori (NTC,
(NTC PTC)
Si tratta di sensori a semiconduttore.
sensori di tipo PTC (Titanato di Bario)
elevato livello di drogaggio: l’aumento della
temperatura implica un aumento della
resistività a causa dell’agitazione termica!!!!
sensori di tipo NTC (nickel, cobalto,
mangaese)
basso livello di drogaggio: ll’aumento
aumento della
temperatura comporta un aumento della
mobilità dei portatori e quindi una diminuzione
della resistività.
R = R0 e
⎛1 1 ⎞
B ⎜⎜ − ⎟⎟
⎝ T To ⎠
con
B T
B=Temperatura
t
caratteristica
tt i ti
R0=Resistenza a 25°C
28
La misura della temperatura
I termistori NTC
R = R0 e
⎛1 1 ⎞
B ⎜⎜ − ⎟⎟
⎝ T To ⎠
I dispositivi a semiconduttore hanno, in genere, una
maggiore sensibilità e un peso minore rispetto agli
RTD.
RTD
Sono altamente non lineari.
Il campo di misura è compreso tra –100°C e 450°C!
La misura della temperatura
I termistori (NTC, PTC)
Un tipico modo di condizionare un termistore:
R=Rpartitore//Rcarico
•La tensione in uscita è non
lineare con la temperatura;
•Comunque
Comunque
scegliendo
opportunamente il valore di
R è possibile linearizzare il
comportamento della rete
resistiva in un range ristretto
di temperature.
La misura della temperatura
I termistori (NTC, PTC)
Alcuni esempi di termistori:
Una tipica applicazione
di un PTC è quella di
protezione
p
per
p
i
sovrariscaldamenti.
La misura della temperatura
I termometri a resistenza: autoriscald.
autoriscald
Quando si usano gli RTD per la misura di temperatura
occorre sempre prestare attenzione all’effetto indotto dal
riscaldamento del sensore. Altrimenti si stimerà un
valore della temperatura in eccesso.
eccesso
E’ possibile tenere conto di tale effetto utilizzando il
fattore di dissipazione termica δ = PD/DT(mW/K).
Esempio: Si supponga di utilizzare un RTD con R=100 Ω e
δ=6 mW/K. Si vuole determinare la corrente massima che si
può inviare al sensore se si vuole che l’errore indotto
dall’autoriscaldamento sia inferiore a 0.1°C.
L’incremento di temperatura necessario a dissipare una certa
potenza vale:
ΔT =
PD
δ
=
I 2R
δ
Quindi la massima corrente varrà:
I=
ΔT δ
=
R
(0.1 °C )(0.006 W / K ) = 2.4 mA
100 Ω
NB: δ dipende dalle condizioni applicative!
32
La misura della temperatura
Le termometria termoelettrica
Effetto Seebeck assoluto
La termometria termoelettrica si basa sull’effetto
Seebeck (1822): Tra due punti, a e b, di un
conduttore M,
conduttore,
M che si trovano a due temperature
diverse è possibile riscontrare una f.e.m.:
a, Ta
M
EM
dEM = σ( T )dT
b, Tb
Tb
EM ( Ta ,Tb ) = ∫ σ( T )dT
Ta
σ dipende dal materiale
materiale.
La misura della temperatura
Le termometria termoelettrica
Le termocoppie:
Si tratta di sensori di temperatura costituiti da due materiali con
un giunto in comune.
a, Ta
M
N
EM
EN
E
b, Tb
c, Tc
Nasce una f.em. Termoelettrica, E, ai capi del
circuito, il cui valore dipende dai metalli e dalla
differenza delle temperature nei terminali e giunti.
giunti
•Si tratta di sensori attivi in quanto generano un segnale in
assenza di sorgenti ausiliarie di energia.
34
La misura della temperatura
Le termometria termoelettrica
Effetto Seebeck relativo
La differenza tra le f.e.m. di Seebeck di due elementi di
una termocoppia il cui giunto comune è a temperatura
Tm e gli altri terminali entrambi a temperatura Tr è la
f.e.m. relativa di Seebeck, così espressa:
a, Tm
M
N
EM
EN
E
b, Tr
c, Tr
E = EM ( Tm ,Tr ) − E N ( Tm ,Tr ) =
Tm
Tm
Tr
Tr
= ∫ σ M dT − ∫ σ N dT
La misura della temperatura
Le termometria termoelettrica
Effetto Seebeck relativo:
a, Tm
M
E = EM ( Tm ,Tr ) − E N ( Tm ,Tr ) =
N
EM
EN
Tm
Tm
Tr
Tr
= ∫ σ M dT − ∫ σ N dT
E
b, Tr
c, Tr
E = f (σ M , σ N ,Tm ,Tr )
con f funzione non lineare.
•Per misurare temperature assolute è necessario
conoscere la temperatura
p
Tr; in q
questo modo la
f.e.m. E sarà funzione della temperatura Tm del
giunto (giunto caldo).
La misura della temperatura
Le termometria termoelettrica
Il modello:
T=a0+a1x+a2x2+a3x3… con x=tensione misurata.
I
parametri
sono
noti
e
reperibili
in
letteratura e si riferiscono ad un valore tipico
e fissato, T0, della temperatura di riferimento
(tipicamente 0°C).
Se
Tr≠T0
si
deve
procedere
ad
una
correzione (compensazione) numerica o
circuitale.
37
La misura della temperatura
Le termometria termoelettrica
Le termocoppie:
•Le termocoppie sono ampiamente impiegate
in numerosi settori dell
dell’automazione
automazione e del
monitoraggio.
•Per un corretto utilizzo è comunque meglio
conoscere un po’ di teoria.
38
La misura della temperatura
Le termometria termoelettrica
•Effetto Peltier: un giunto tra due materiali diversi
su cui scorre una corrente si riscalda o si raffredda
in base al verso della corrente; per un giunto a
temperatura T si ha:
π AB = T ( S B − S A ) = −π BA
dove πAB rappresenta il calore liberato dalla
giunzione AB per ogni unità di corrente che
transita da B verso A.
N.B.: Per convenzione il contribuo energetico
dovuto a calore liberato nell’ambiente si
considererà negativo.
La misura della temperatura
Le termometria termoelettrica
•Effetto
Effetto Thomson: un conduttore omogeneo con una
temperatura non omogenea, in cui scorre corrente,
si riscalda o si raffredda in base al verso della corrente.
In particolare, se il verso della corrente corrisponde
al flusso termico allora il conduttore libera calore.
dT
q = i r − iσ
dx
2
dove q è il flusso di calore per unità di volume, r è la
resistività del conduttore e σ è il coefficiente di
Thomson.
La misura della temperatura
Le termometria termoelettrica
Realistic Thermocouple Circuits
•The true nature of the Seebeck phenomenon
is the occurrence of a source emf that, for
accurate thermometry, must be measured in
open-circuit mode that suppresses current.
•In practical thermometry, no realistic
thermocouple circuit has only two dissimilar
materials. Some have many dissimilar
materials
t i l
and
d severall off these
th
can be
b
expected to contribute some Seebeck emf.
e most
os co
common
o thermometry
e o e y ccircuits
cu s have
a e
•The
two separate reference junctions, not one.
41
La misura della temperatura
Le termometria termoelettrica
Singola giunzione di riferimento
EA’
EB
EA
E
•Questa
Q
t configurazione
fi
i
è utile
til per misure
i
molto
lt accurate
t in
i
laboratorio in cui il giunto di riferimento può essere tenuto a
temperatura costante ad esempio in bagno di ghiaccio.
Deve essere:
•Ti=Ta=Tf: affinché i gradienti all’interno dello strumento (sezione
tratteggiata) di misura non diano origine a f.e.m. di Seebeck.
Tc=T
Td: affinché il materiale intermedio C non dia origine a f.e.m.
•T
di Seebeck;
•In questo caso si ha:
Tr
Tm
Ti
Ti
Tr
Tm
E = E A' + EB + E A = ∫ σ A dT + ∫ σ B dT + ∫ σ A dT =
Tm
Tr
Tm
Tm
= ∫ σ B dT + ∫ σ A dT = ∫ σ B dT − ∫ σ A dT =
Tr
Tm
Tr
Tr
Tm
∫ (σ
Tr
B
− σ A )dT
42
La misura della temperatura
Le termometria termoelettrica
Sulla base di quanto detto sono possibili diversi
schemi di misura:
•Metodi con giunto freddo alla temperatura di riferimento
IIn questo
t caso sii è voluto
l t utilizzare
tili
un materiale
t i l meno
prezioso per effettuare I collegamenti!!!
Esempio: Si supponga di utilizzare una termocoppia con
giunto freddo a 20
20°C
C e giunto caldo a 100
100°C
C. Sapendo che la
forza elettromotrice sviluppata a 20°C e di 0,79 mV e di 4,28
mV a 100 °C. Nel caso in esame verrà prodotta una emf pari a:
4,28-0,79= 3,49 mV
•Un’altra possibilità è quella di lasciare il giunto di
riferimento (freddo) alla temperatura ambiente
qualora quest’ultima varia molto poco rispetto alla
risoluzione desiderata, oppure
•Si misura questa temperatura ambiente a cui è
soggetto il giunto di riferimento e si effettua una
compensazione.
43
La misura della temperatura
Le termometria termoelettrica
Circuito con due giunzioni di riferimento
Ts
•In questo caso la f.e.m. in ingresso allo strumento dipende dalla
Tm e dalla Temperatura dei giunti di riferimento (i due giunti
devono stare alla stessa temperatura).
temperatura)
•C e D sono conduttori utilizzati per portare il segnale in ingresso
allo strumento (extension leads).
•In base al tipo di conduttori utilizzati (C e D) i giunti di
riferimento possono essere e,c oppure b,f.
•All’interno
All’interno dello strumento esiste un sistema per compensare la
temperatura dei giunti di riferimento.
Ad esempio si può misurare tale temperatura e si può apportare
la correzione per compensare lo scarto tra Tr e T0.
44
La misura della temperatura
Le termometria termoelettrica
Circuito con due giunzioni di riferimento
•I giunti di riferimento
possono essere e,c
oppure b,f.
1) C e D Neutral Extension Leads: sono materiali uguali con lo
stesso coefficiente Seebeck, σc= σD e quindi producono due
f.e.m. che si compensano. In questo caso i giunti di riferimento
sono e, c.
E = ED + E B − E A − EC =
Ts
Tm
Tm
Ts
Ti
Ts
Ts
Ti
= ∫ σ D dT + ∫ σ B dT − ∫ σ A dT − ∫ σ C dT
45
La misura della temperatura
Le termometria termoelettrica
Circuito con due giunzioni di riferimento
•I giunti di riferimento
possono essere e,c
oppure b,f.
2) C e D Matching Extension Leads: σc= σA e σB= σD
E = ED + EB − E A − EC =
Ts
Tm
Tm
Ts
Ti
Ts
Ts
Ti
Tm
Tm
Ti
Ti
= ∫ σ D dT + ∫ σ B dT − ∫ σ A dT − ∫ σ C dT =
= ∫ σ B dT − ∫ σ A dT
In questo caso i giunti di riferimento sono b,
b f.
f
46
La misura della temperatura
Le termometria termoelettrica
Circuito con due giunzioni di riferimento
•I giunti di riferimento
possono essere e,c
oppure b,f.
3) C e D Compensating Extension Leads: si scelgono i
materiali C e D in modo che σCD= σAB. In questo caso i giunti di
riferimento sono b, f.
Il vantaggio di questa soluzione è che i conduttori C e D non
devono essere pregiati ma solo tali da rispettare la precedente
condizione sui coeff. di Seebeck.
E = ED + EB − E A − EC =
Ts
Ts
Tm
Tm
Ti
Ti
Ts
Ts
= ∫ σ D dT − ∫ σC dT + ∫ σ B dT − ∫ σ A dT =
Ts
Tm
Tm
Ti
Ts
Ti
= ∫ σCD dT − ∫ σ AB dT = ∫ σ AB dT
47
La misura della temperatura
Termocoppie: la compens. del giunto freddo
a Tm
a,
Fe
EFe E
Cn
Cn
VFeCn
b, Tr
c, Ta
La relazione tabulata tra la tensione VFeCn fornita da una
termocoppia e la temperatura del giunto caldo è riferita ad una
T di riferimento pari a 0.
Se il giunto freddo si trova ad una temperatura, Ta, differente
da zero è necessario sommare alla VFeCn una tensione p
pari a
quella che fornirebbe la termocoppia quando il giunto caldo si
trova a Ta (ed il giunto freddo a zero).
Ad esempio: se giunto caldo e freddo sono alla stessa
temperatura Ta
Ta, si ha VFeCn=0,
=0 mentre si dovrebbe avere il
valore tabulato per Ta:
VFeCn
Ta
A tale scopo si implementa un meccanismo di compensazione
che consiste nel sommare una Vb alla VFeCn
F C :
V= VFeCn +Vb
dove Vb è la tensione che fornirebbe la termocoppia con il
giunto di riferimento a zero gradi.
48
La misura della temperatura
Termocoppie: la compens. del giunto freddo
Fig. 6.1
Es. termocoppia FeCn
V = VFeCn + Vb
⎡ R1'
R ⎤
Vb = −VR ⎢ '
− ' 4 ⎥
⎣ R1 + R2 R3 + R4 ⎦
R1' = R1 + R0 ( 1 + αT )
Vb = VFeCn T con approssimazione lineare si ha
a
Vb = KTa + c
dVb
=K
dT
Supponiamo che la termocoppia sia di tipo J e che si voglia
compensare in un range 10°C-40°C:
10 C 40 C:
dalla tabella 6.2 (Webster) si può stimare nel range indicato:
K=52μV/°C;
Inoltre due condizioni per fissare I parametri liberi possono
essere:
Vb(0)=0 (perchè a 0°C la VFeCn=0) e quindi c=0;
e Vb ( 25°C ) = − VCnFe 25°C = 1.3mV
Per fissare un altro punto di lavoro tipico della termocoppia.
49
La misura della temperatura
Le termometria termoelettrica
Sebbene si possano costruire infinite
termocoppie, solo alcune combinazioni
danno origine a dispositivi utilizzabili. In
particolare occorre soddisfare i seguenti
requisiti:
•La compatibilità
p
tra i fili;;
• L’ omogeneità e la stabilità;
•La sensibilità;
Le termocoppie più utilizzate sono:
•rame/costantana (T)
•ferro/costantana (J)
•nickel-cromo/nickel-alluminio (K)
•platino/rodio (R,S,B)
•tungsteno/renio
La misura della temperatura
Le termometria termoelettrica
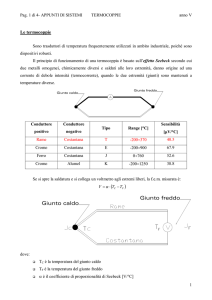
Si riportano le principali caratteristiche
delle termocoppie.
T
J
K
51
La misura della temperatura
Le termometria termoelettrica
Si riportano le principali caratteristiche
delle termocoppie.
52
53
La misura della temperatura
Le termometria termoelettrica
Le norme (IEC 548) specificano le caratteristiche
principali delle termocoppie e i rispettivi tipi di
tolleranza
(termocoppie
di
classe
II
e
t
termocoppie
i di classe
l
I) utilizzando
I),
tili
d opportuni
t i
polinomi interpolanti i cui coefficienti sono
tabulati.
La misura della temperatura
Le termometria termoelettrica
La termometria termoelettrica è regolata
da tre leggi.
•Legge
Legge dei circuiti omogenei:
Non è possibile indurre una corrente
termoelettrica in un conduttore omogeneo
solamente riscaldandolo.
riscaldandolo
•Quindi temperature intermedie su un conduttore non alterano
la f.e.m. dovuta alla differenza di T tra due giunti.
55
La misura della temperatura
Le termometria termoelettrica
Legge dei metalli intermedi:
La somma algebrica delle f.e.m. in un circuito copmposto da
diversi metalli è zero fino a quando tutto il circuito è alla
stessa temperatura.
Corollario: se è nota la relazione termica tra due materiali
ed un terzo è possibile dedurre la relazione termica tra i
primi due.
Fig.6.8
56
La misura della temperatura
Le termometria termoelettrica
•Legge delle temperature successive.
Se due metalli mostrano una f.e.m. E1
quando le loro giunzioni si trovano alle due
temperature T1 e T2, e ad una f.e.m. E2
quando le loro giunzioni si trovano alle due
temperature T2 e T3,allora la f.e.m. che si
ottiene quando le giunzioni si trovano alle
temperature T1 e T3 è: E1+E2.
57
La misura della temperatura
Le termometria termoelettrica
Utilizzando le precedenti relazioni è facile
dimostrare che:
• la serie di
sensibilità
termocoppie
aumenta
la
•il parallelo tra termocoppie restituisce una
stima del valore medio di temperatura.
temperatura
58
La misura della temperatura
La termometria a radiazione
OGNI CORPO A TEMPERATURA SUPERIORE
ALLO ZERO ASSOLUTO EMETTE RADIAZIONI
ELETTROMAGNETICHE
La
termometria
a radiazione trae
origine da due leggi:
•La
La
legge di Stefan-Boltzmann
Stefan Boltzmann che
fornisce il valore della radianza totale
• La legge di Plank che definisce la
radianza spettrale
La misura della temperatura
La termometria a radiazione
Legge di Stefan-Boltzmann
per un corpo nero:
WCN= 5.67
5 67 ⋅ 10-12 T4 [W/cm2]
per corpi radianti reali:
emissività
4
2
W= 5.67
5 67 ⋅ 10-12 εtot,T
t t T T [W/cm ]
Emissività totale
ε tot,T
ε =1
ε <1
W
1
W
=
=
⋅ 4
−12
WCN 5.67 ⋅10 T
corpo nero
corpo reale
La misura della temperatura
La termometria a radiazione
L’emissività di alcuni corpi
La misura della temperatura
La termometria a radiazione
Legge di Planck per un corpo reale:
C1ελ ,T
Wλreale = 5 C2 λT
πλ ( e
−1 )
−12
C1 = 3.7410 Wcm
C2 = 1.44cmK
2
La misura della temperatura
La termometria a radiazione
Legge di Wien per un corpo reale:
λ Max
2898
=
T
La misura della temperatura
La termometria a radiazione
•Il pirometro
monocromatico
Il principio di funzionamento si basa sulla legge di
Planck che afferma che il colore di una superfircie
cambia con la temperatura.
Dall’oculare è possibile osservare una riga (dovuta alla
lampada) sull’immagine proveniente dalla sorgente.
Quando la riga scompare le temperature del filamento e
della sorgente sono uguali ed è quindi possibile riferire il
valore della temperatura incognita al valore della
corrente sul filamento.
La misura della temperatura
La termometria a radiazione
Versione
fotoelettrica
monocromatico.
del
pirometro
Essa
ssa co
consente:
se e:
•Il raggiungimento automatico delle condizioni di
equilibrio;
•Risoluzione più elevata e stima più oggettiva
•Il funzionamento a lunghezze d’onda non visibili
(temperature inferiori).
La misura della temperatura
La termometria a radiazione
PIROMETRO A DUE COLORI
Si
basa sullo schema del pirometro
mocromatico, non vi è più la lampada ma
due filtri che lasciano passare la radiazione
termica in due bande molto strette attorno a
due luinghezze d’onda molto vicine.
Dalla legge di Planck per corpi reali si ha:
Wλreale =
ελ
=
ελ
Wλ
•
•
Wλ1
1
2
2
C1ε λ ,T
λT
λ5 (eC
2
5
⎛ λ2 ⎞
⋅ ⎜⎜ ⎟⎟ e
⎝ λ1 ⎠
−1)
C2 ⎛ 1 1 ⎞
⋅⎜ − ⎟
T ⎜⎝ λ2 λ1 ⎟⎠
5
⎛ λ2 ⎞
≈ ⎜⎜ ⎟⎟ e
⎝ λ1 ⎠
C2 ⎛ 1 1 ⎞
⋅⎜ − ⎟
T ⎜⎝ λ2 λ1 ⎟⎠
Misurate le due radianze e note le lunghezze d’onda,
è possibile risalire al valore di T.
Le due lunghezze d’onda devono essere molto vicine
affinchè l’emissività non cambi;
La misura della temperatura
La termometria a radiazione
PIROMETRO A DUE COLORI
• Indipendenza dall’emissività;
• Immunità a corpi trasparenti (fumi, ect.)
interposti tra lo strumento ed il target perché
non alterano la relazione precedente.
p
• Meno
accurato
monocromatico,
• Utile per applicazioni
ambienti ostili
del
pirometro
industriali
ed
La misura della temperatura
La termometria a radiazione
Radiometro
Questo strumento misura la temperatura sulla
b
base
d
deglili effetti
ff tti della
d ll radiazione
di i
su una banda
b d
molto più grande rispetto alle bande ristrette dei
due strumenti precedenti.
Aumentare la banda permette la misura di
temperature più basse, a cui corrispondono
radiazioni più basse, che negli strumenti
precedenti produrrebbero un segnale
fotoelettrico troppo basso.
La misura della temperatura
La termometria a radiazione
Radiometro
Come sensore sii utilizza
C
tili
una termopila
t
il che
h ffornisce
i
una
tensione proporzionale alla temperatura di radiazione.
Le termopile sono meno sensibili delle celle fotoelettriche ma
sono sensibili in un intervallo molto ampio di lunghezze d’onda
(estensione del campo di misura).
V = k1(T1-T2) = k2(Trad)4
Chopped e Unchopped