Triangoli rettangoli con angoli da 30, 60 e 45 gradi

Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 1
Raccolta di problemi di geometra piana sul teorema di Pitagora applicato ai triangoli con
angoli di 45°, 30° e 60°. Completi di soluzione guidata.
Triangle Problems involving Pythagoras Theorem. (Geometry)
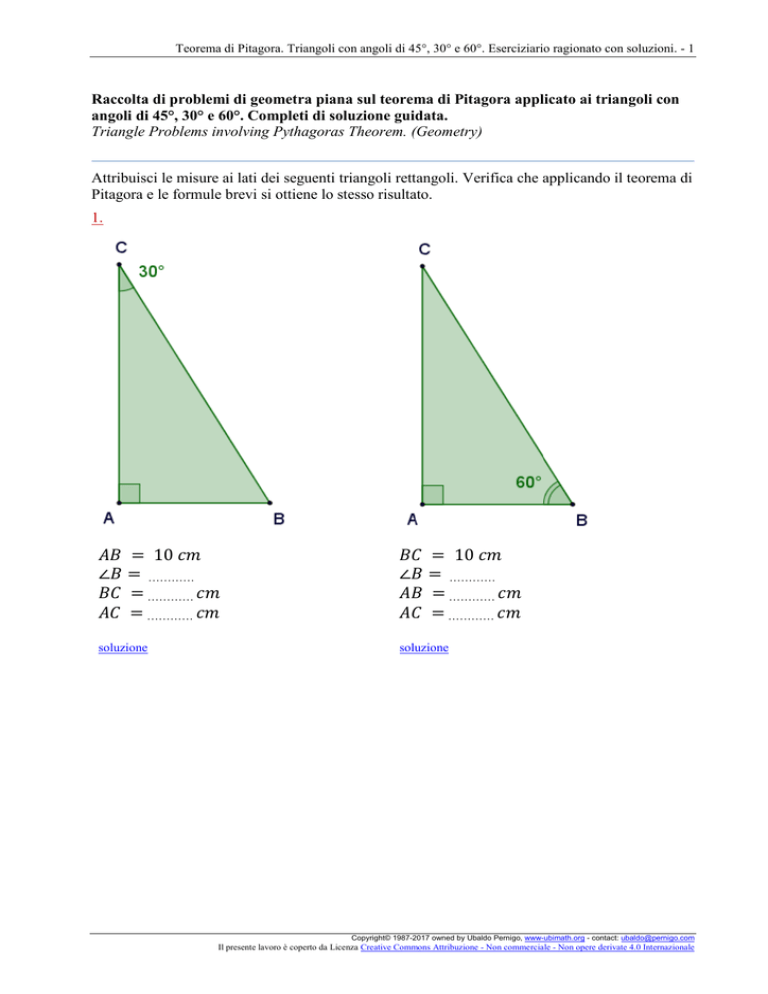
Attribuisci le misure ai lati dei seguenti triangoli rettangoli. Verifica che applicando il teorema di
Pitagora e le formule brevi si ottiene lo stesso risultato.
1.
𝐴𝐵
∠𝐵
𝐵𝐶
𝐴𝐶
= 10 𝑐𝑚
= …………
= ………… 𝑐𝑚
= ………… 𝑐𝑚
soluzione
𝐵𝐶
∠𝐵
𝐴𝐵
𝐴𝐶
= 10 𝑐𝑚
= …………
= ………… 𝑐𝑚
= ………… 𝑐𝑚
soluzione
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 2
2.
𝐴𝐵 = 10 𝑐𝑚
∠𝐶 = …………
𝐵𝐶 = ………… 𝑐𝑚
𝐴𝐶 = ………… 𝑐𝑚
𝐵𝐶
∠𝐵
𝐴𝐵
𝐴𝐶
= 30 𝑐𝑚
= …………
= ………… 𝑐𝑚
= ………… 𝑐𝑚
soluzione
Usa per allinearti i simulatori, nati per Alice, e che trovi on line per esercitarti ai collegamenti seguenti:
>> www.ubimath.org/geogebra/TriangoloRettangolo454590_UbiMath2017.ggb
>> www.ubimath.org/geogebra/TriangoloRettangolo306090_UbiMath2017.ggb
3. Un triangolo rettangolo ABC, rettangolo in A, ha l’angolo acuto in B di 45° e il suo cateto AB
misura 20 cm. Calcola il perimetro e l’area del triangolo.
soluzione
4. Un triangolo rettangolo ABC, rettangolo in A, è isoscele e la sua ipotenusa BC misura 2√2
cm. Calcola il perimetro e l’area del triangolo.
soluzione
5. Un triangolo rettangolo ABC, rettangolo in A, ha l’angolo in C di 30° e l’ipotenusa BC
misura 16 cm. Calcola il perimetro e l’area del triangolo.
soluzione
6. Un triangolo rettangolo ABC, rettangolo in A, ha l’angolo in B di 60° e il cateto minore AB
che misura 16 cm. Calcola il perimetro e l’area del triangolo.
soluzione
7. Un triangolo rettangolo ABC, rettangolo in A, ha l’angolo in B di 60° e il cateto maggiore AC
che misura 4√3 cm. Calcola il perimetro e l’area del triangolo.
soluzione
8. Un triangolo rettangolo in A ha l’angolo in B di 60°. Sapendo che la lunghezza della sua
ipotenusa BC è di 20 cm, calcola il perimetro e l’area del triangolo rettangolo.
soluzione
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 3
9. Un triangolo scaleno ABC ha l’angolo in corrispondenza del vertice A ampio 30° e quello nel
vertice B di 45°. Sapendo che l’altezza CH, relativa al lato AB, è lunga 20 cm, determina l’area e
il perimetro del triangolo.
soluzione
10. Un triangolo rettangolo ABC, rettangolo in A, l’ipotenusa BC, che è il doppio del cateto
minore AB, misura 8 cm. Calcola il perimetro e l’area del triangolo.
soluzione
11. Un triangolo rettangolo ABC, rettangolo in A, l’ipotenusa BC è il doppio del cateto minore
AB e il cateto maggiore AC misura 2√3 cm. Calcola il perimetro e l’area del triangolo.
soluzione
12. Un triangolo rettangolo ABC, rettangolo in A, ha i due angoli acuti uguali e la sua ipotenusa
BC misura 6√2 cm. Calcola il perimetro e l’area del triangolo.
soluzione
13. Un triangolo rettangolo ABC, rettangolo in A, ha l’angolo in B che il doppio dell’angolo in
C e il cateto maggiore AC che misura 6√3 cm. Calcola il perimetro e l’area del triangolo.
soluzione
14. Un triangolo rettangolo ABC, rettangolo in A, ha i due angoli acuti da 45° e la sua ipotenusa
BC misura 6√2 cm. Calcola il perimetro e l’area del triangolo.
soluzione
15. Un triangolo rettangolo ABC, rettangolo in A, è isoscele e il suo cateto AB misura 12 cm.
Calcola il perimetro e l’area del triangolo.
soluzione
16. In un triangolo ABC l’altezza CH, lunga 24 cm, forma con il lato AC un angolo di 60° e con
il lato BC un angolo di 45°. Calcolate il perimetro e l’area del triangolo dato.
soluzione
17. In un triangolo isoscele ABC l’angolo al vertice è di 120° e uno dei lati uguali misura 4 m.
Calcolate il perimetro e l’area del triangolo dato.
soluzione
18. Un trapezio isoscele ha i due angoli acuti alla base di 60°. Sapendo che la base maggiore
misura 16 m e la minore 10 m calcola il perimetro e l’area del trapezio dato.
soluzione
19. Un trapezio isoscele ha i due angoli acuti alla base di 30°. Sapendo che la base minore
misura 20 cm e il lato obliquo 40 cm calcola il perimetro e l’area del trapezio dato.
soluzione
20. Un trapezio isoscele ha i due angoli acuti alla base di 45°. Sapendo che l’altezza del trapezio
misura 12 cm e che la base minore congruente a questa calcola il perimetro e l’area del trapezio
dato.
soluzione
21. Un rombo è formato da due triangoli equilateri sovrapposti. Sapendo che il perimetro del
rombo misura 120 m calcola l’area della figura.
soluzione
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 4
Soluzioni
AB = 10 cm
∠𝐴 = 90°
∠𝐶 = 30°
La somma degli angoli interni di un triangolo è un angolo di
180°.
∠𝐴 + ∠𝐵 + ∠𝐶 = 180°
Il triangolo rettangolo ha l’altro angolo di 30° (180°-60°) ed
è la metà di un triangolo equilatero.
𝐶𝐵 = 2 ∙ 𝐴𝐵 = 20 𝑐𝑚
𝐴𝐵 =
𝑙
√3 = 10√3 𝑐𝑚
2
𝐶𝐵 = 2 ∙ 𝐴𝐵 = 20 𝑐𝑚
Applico il teorema di Pitagora
𝐴𝐵 = √𝐶𝐵 2 − 𝐴𝐵 2
𝐴𝐵 = √202 − 102 = √300 cm
Applico le proprietà dei radicali
𝐴𝐵 = √3 ∙ 100 = √3 ∙ √100 = 10√3𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 5
BC = 10 cm
∠𝐴 = 90°
∠𝐵 = 60°
La somma degli angoli interni di un triangolo è un angolo di
180°.
∠𝐴 + ∠𝐵 + ∠𝐶 = 180°
Il triangolo rettangolo ha l’altro angolo di 60° (180°-30°) ed
è la metà di un triangolo equilatero.
1
1
𝐵𝐶 = 10 = 5 𝑐𝑚
2
2
𝑙
𝐴𝐶 = √3 = 5√3 𝑐𝑚
2
𝐴𝐵 =
1
1
𝐵𝐶 = 10 = 5 𝑐𝑚
2
2
Applico il teorema di Pitagora
𝐴𝐵 =
𝐴𝐶 = √𝐶𝐵 2 − 𝐴𝐵 2
𝐴𝐶 = √102 − 52 = √75 cm
Applico le proprietà dei radicali
𝐴𝐵 = √3 ∙ 25 = √3 ∙ √25 = 5√3 𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 6
AB = 20 cm
∠𝐴 = 90°
∠𝐵 = 45°
La somma degli angoli interni di un triangolo è un angolo di
180°.
∠𝐴 + ∠𝐵 + ∠𝐶 = 180°
Il triangolo rettangolo ha l’altro angolo di 45° (180°-45°) ed
è isoscele e la sua ipotenusa è la diagonale di un quadrato
che ha per lati i cateti.
𝐴𝐶 = 𝐴𝐵 = 20 𝑐𝑚
𝐴𝐶 = 𝐴𝐵 = 20 𝑐𝑚
𝐴𝐵 = 𝑙√2 = 20√2 𝑐𝑚
Applico il teorema di Pitagora
𝐴𝐶 = √𝐴𝐵 2 + 𝐴𝐶 2
𝐴𝐶 = √202 + 202 = √800 cm
Applico le proprietà dei radicali
𝐴𝐵 = √2 ∙ 202 = √2 ∙ √202 = 20√2 𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 7
Un triangolo rettangolo ABC, rettangolo in A, ha l’angolo
acuto in B di 45° e il suo cateto AB misura 20 cm. Calcola il
perimetro e l’area del triangolo.
Dati e relazioni
𝐴̂ = 90°
𝐵̂ = 45°
𝐴𝐵 = 20 𝑐𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝;
2. 𝐴𝑟𝑒𝑎
𝐶̂ = 180° − (𝐴̂ + 𝐵̂ ) = 180° − (90° + 45°) = 45°
Un triangolo rettangolo con due angoli di 45° è isoscele.
𝐴𝐵 = 𝐴𝐶 = 𝑐1 = 𝑐2 = 20 𝑐𝑚
𝐵𝐶 = 𝑖 = √𝐴𝐵 2 + 𝐴𝐶 2 =
𝐵𝐶 = √202 + 202 = √400 + 400 = √400 ∙ 2 = 20√2 𝑐𝑚
𝑏 ∙ ℎ 𝐴𝐵 ∙ 𝐴𝐶 20 ∙ 20
=
=
= 200 𝑐𝑚2
2
2
2
2𝑝 = 𝐴𝐵 + 𝐵𝐶 + 𝐴𝐶
𝐴=
2𝑝 = 20 + 20 + 20√2 = (40 + 20√2 ) 𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 8
Un triangolo rettangolo ABC, rettangolo in A, è isoscele e la sua
ipotenusa BC misura 2√2 cm. Calcola il perimetro e l’area del
triangolo.
Dati e relazioni
𝐴̂ = 90°
𝐵̂ = 𝐶̂
𝐴𝐵 = 𝐴𝐶
𝐵𝐶 = 2√2 𝑐𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝;
2. 𝐴𝑟𝑒𝑎
180° − 90° 90°
=
= 45°
2
2
Un triangolo rettangolo con due angoli di 45° è isoscele.
𝐵̂ = 𝐶̂ =
Essendo per il Teorema di Pitagora il quadrato costruito
sull’ipotenusa somma di due quadrati uguali costruiti sui cateti, è
possibile trovare il lato di uno dei quadrati costruiti sui cateti …
𝐴𝐵 = 𝐴𝐶 = 𝑐1 = 𝑐2 = √
𝐶𝐵 2 √(2√2)2
4∙2
=
=√
= 2 𝑐𝑚
2
2
2
𝑏 ∙ ℎ 𝐴𝐵 ∙ 𝐴𝐶 2 ∙ 2
=
=
= 2 𝑐𝑚2
2
2
2
2𝑝 = 𝐴𝐵 + 𝐵𝐶 + 𝐴𝐶
𝐴=
2𝑝 = 2 + 2 + 2√2 = (4 + 2√2 ) 𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 9
Un triangolo rettangolo ABC, rettangolo in A, ha l’angolo in C di 30° e
l’ipotenusa BC misura 16 cm. Calcola il perimetro e l’area del triangolo.
Dati e relazioni
𝐴̂ = 90°
𝐶̂ = 30°
𝐵𝐶 = 16 𝑐𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝; 2. 𝐴𝑟𝑒𝑎
𝐵̂ = 180° − (𝐴̂ + 𝐶̂ ) = 180° − (90° + 30°) = 60°
Un triangolo rettangolo che ha due angoli di 30° e di 60° è la metà di un
triangolo equilatero. Il lato maggiore, l’ipotenusa, è quindi il doppio del
cateto minore.
Si può applicare, quindi, il Teorema di Pitagora …
𝐴𝐵 = 𝑐1 =
𝐵𝐶 16
=
= 8 𝑐𝑚
2
2
𝐴𝐶 = 𝑐2 = √𝐶𝐵 2 − 𝐴𝐵 2
𝐴𝐶 = √162 − 82 = √256 − 64 = √192 = √64 ∙ 3 = 8√3 𝑐𝑚
𝐴=
𝑏 ∙ ℎ 𝐴𝐵 ∙ 𝐴𝐶 8 ∙ 8√3
=
=
= 32√3 𝑐𝑚2
2
2
2
2𝑝 = 𝐴𝐵 + 𝐵𝐶 + 𝐴𝐶 = 8 + 16 + 8√3 = (24 + 8√3 ) 𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 10
Un triangolo rettangolo ABC, rettangolo in A, ha l’angolo in B di 60° e
il cateto minore AB che misura 16 cm. Calcola il perimetro e l’area del
triangolo.
Dati e relazioni
𝐴̂ = 90°
𝐵̂ = 60°
𝐴𝐵 = 16 𝑐𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝; 2. 𝐴𝑟𝑒𝑎
𝐶̂ = 180° − (𝐴̂ + 𝐵̂ ) = 180° − (90° + 60°) = 30°
Un triangolo rettangolo che ha due angoli di 30° e di 60° è la metà di un
triangolo equilatero. Il lato maggiore, l’ipotenusa, è quindi il doppio del
cateto minore.
Si può applicare, quindi, il Teorema di Pitagora …
𝐵𝐶 = 𝑖 = 2 ∙ 𝐴𝐵 = 2 ∙ 𝑐1 = 2 ∙ 16 = 32 𝑐𝑚
𝐴𝐶 = 𝑐2 = √𝐶𝐵 2 − 𝐴𝐵 2
𝐴𝐶 = √322 − 16 = √1024 − 256 = √768 = √256 ∙ 3 = 16√3 𝑐𝑚
𝐴=
𝑏 ∙ ℎ 𝐴𝐵 ∙ 𝐴𝐶 16 ∙ 168 √3
=
=
= 128√3 𝑐𝑚2
2
2
2
2𝑝 = 𝐴𝐵 + 𝐵𝐶 + 𝐴𝐶 = 16 + 32 + 16√3 = (48 + 16√3 ) 𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 11
Un triangolo rettangolo ABC, rettangolo in A, ha l’angolo in B di 60° e
il cateto maggiore AC che misura 4√3 cm. Calcola il perimetro e l’area
del triangolo.
Dati e relazioni
𝐴̂ = 90°
𝐵̂ = 60°
𝐴𝐶 = 4√3 𝑐𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝; 2. 𝐴𝑟𝑒𝑎
𝐶̂ = 180° − (𝐴̂ + 𝐵̂ ) = 180° − (90° + 60°) = 30°
Un triangolo rettangolo che ha due angoli di 30° e di 60° è la metà di un
triangolo equilatero. Il lato maggiore, l’ipotenusa, è quindi il doppio del
cateto minore.
Essendo per il Teorema di Pitagora il quadrato costruito sull’ipotenusa
4 volte il quadrato costruito sul cateto minore, è possibile trovare il lato
del quadrato costruito sul cateto minore sapendo che questo quadrato
ha area pari a un terzo di quella costruita sull’altro cateto …
𝐴𝐵 =
𝐴𝐶
𝐴𝐶 2
(4√3)2
16 ∙ 3
= 𝑐1 = √
=√
=√
= 4 𝑐𝑚
2
3
3
3
𝐵𝐶 = 𝑖 = 2 ∙ 𝐴𝐵 = 2 ∙ 𝑐1 = 2 ∙ 4 = 8 𝑐𝑚
𝐴=
𝑏 ∙ ℎ 𝐴𝐵 ∙ 𝐴𝐶 4 ∙ 4√3
=
=
= 8√3 𝑐𝑚2
2
2
2
2𝑝 = 𝐴𝐵 + 𝐵𝐶 + 𝐴𝐶 = 4 + 8 + 4√3 = (12 + 4√3 ) 𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 12
Un triangolo rettangolo in A ha l’angolo in B di 60°. Sapendo che la
lunghezza della sua ipotenusa BC è di 20 cm, calcola il perimetro e
l’area del triangolo rettangolo.
Dati e relazioni
𝐴̂ = 90°
𝐵̂ = 60°
𝐵𝐶 = 20 𝑐𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝; 2. 𝐴𝑟𝑒𝑎
𝐶̂ = 180° − (𝐴̂ + 𝐵̂ ) = 180° − (90° + 60°) = 30°
Un triangolo rettangolo che ha due angoli di 30° e di 60° è la metà di un
triangolo equilatero. Il lato maggiore, l’ipotenusa, è quindi il doppio del
cateto minore.
Si può applicare, quindi, il Teorema di Pitagora …
𝐴𝐵 = 𝑐1 =
𝐵𝐶 20
=
= 10 𝑐𝑚
2
2
𝐴𝐶 = 𝑐2 = √𝐶𝐵 2 − 𝐴𝐵 2
𝐴𝐶 = √202 − 102 = √400 − 100 = √300 = √100 ∙ 3 = 10√3 𝑐𝑚
𝐴=
𝑏 ∙ ℎ 𝐴𝐵 ∙ 𝐴𝐶 10 ∙ 10√3
=
=
= 50√3 𝑐𝑚2
2
2
2
𝐴 = 50√3 𝑐𝑚2 ≈ 86,60 𝑐𝑚2
2𝑝 = 𝐴𝐵 + 𝐵𝐶 + 𝐴𝐶
2𝑝 = 10 + 20 + 10√3 = (30 + 10√3 ) 𝑐𝑚
2𝑝 = (30 + 10√3 ) 𝑐𝑚 ≈ 47,32 𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 13
Un triangolo scaleno ABC ha l’angolo in corrispondenza del vertice A
ampio 30° e quello nel vertice B di 45°. Sapendo che l’altezza CH,
relativa ala lato AB, è lunga 20 cm, determina l’area e il perimetro del
triangolo.
Dati e relazioni
𝐴̂ = 30°
𝐵̂ = 45°
𝐶 𝐻 = 20 𝑐𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
Perimetro, area
̂ + 𝐵̂ ) = 180° − (90° + 45°) = 45°
𝐻𝐶̂ 𝐵 = 180° − (𝐻
̂ + 𝐴̂) = 180° − (90° + 30°) = 60°
𝐻𝐶̂ 𝐵 = 180° − (𝐻
Un triangolo rettangolo con due angoli di 45° è isoscele.
Un triangolo rettangolo che ha due angoli di 30° e di 60° è la metà di un
triangolo equilatero. Il lato maggiore, l’ipotenusa, è quindi il doppio del
cateto minore.
Se A^=30° allora ACH^=60° e AC=2CH
𝐴𝐶 = 2𝐶𝐻 = 2 ∙ 20 = 40 𝑐𝑚
𝐴𝐻 = √𝐴𝐶 2 − 𝐶𝐻 2 = √402 − 202 = √1200 = 20√3 𝑐𝑚
𝐴𝐵 = 𝐴𝐻 + 𝐵𝐻 = (20√3 + 20)𝑐𝑚
Se B^=45° allora BCH^=45° e BH = CH = 20 cm
180° − (90° + 45°) = 45°
Un triangolo rettangolo con due angoli di 45° è isoscele.
𝐶𝐵 = √𝐵𝐻 2 + 𝐶𝐻 2
𝐶𝐵 = √202 + 202 = √800 = 20√2 𝑐𝑚
𝐴=
𝐴𝐵 ∙ 𝐶𝐻 (20√3 + 20) ∙ 20
=
= (200√3 + 200)𝑐𝑚2
2
2
𝐴𝐵 ∙ 𝐶𝐻 (20√3 + 20) ∙ 20 54,64 ∙ 20
=
=
= 546,4 𝑐𝑚2
2
2
2
2𝑝 = 𝐴𝐵 + 𝐶𝐵 + 𝐴𝐶
𝐴=
2𝑝 = 20√3 + 20 + 20√2 + 40 = (60 + 20√2 + 20√3)𝑐𝑚
2𝑝 = (60 + 28,28 + 34,64)𝑐𝑚 ≈ 122,92 𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 14
Un triangolo rettangolo ABC, rettangolo in A, l’ipotenusa BC, che è il
doppio del cateto minore AB, misura 8 cm. Calcola il perimetro e l’area
del triangolo.
Dati e relazioni
𝐴̂ = 90°
𝐵𝐶 = 2 ∙ 𝐴𝐶
𝐵𝐶 = 8 𝑐𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝;
2. 𝐴𝑟𝑒𝑎
Un triangolo rettangolo che ha due angoli di 30° e di 60° è la metà di un
triangolo equilatero. Il lato maggiore, l’ipotenusa, è quindi il doppio del
cateto minore.
Si può applicare, quindi, il Teorema di Pitagora …
𝐴𝐵 = 𝑐1 =
𝐵𝐶 8
= = 4 𝑐𝑚
2
2
𝐴𝐶 = 𝑐2 = √𝐶𝐵 2 − 𝐴𝐵 2
𝐴𝐶 = √8 − 42 = √64 − 16 = √48 = √16 ∙ 3 = 4√3 𝑐𝑚
𝐴=
𝑏 ∙ ℎ 𝐴𝐵 ∙ 𝐴𝐶 4 ∙ 4√3
=
=
= 8√3 𝑐𝑚2
2
2
2
2𝑝 = 𝐴𝐵 + 𝐵𝐶 + 𝐴𝐶 = 4 + 8 + 4√3 = (12 + 4√3 ) 𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 15
Un triangolo rettangolo ABC, rettangolo in A, l’ipotenusa BC è il
doppio del cateto minore AB e il cateto maggiore AC misura 2√3 cm.
Calcola il perimetro e l’area del triangolo.
Dati e relazioni
𝐴̂ = 90°
𝐵𝐶 = 2 ∙ 𝐴𝐵
𝐴𝐶 = 2√3 𝑐𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝; 2. 𝐴𝑟𝑒𝑎
Un triangolo rettangolo che ha due angoli di 30° e di 60° è la metà di un
triangolo equilatero. Il lato maggiore, l’ipotenusa, è quindi il doppio del
cateto minore.
Essendo per il Teorema di Pitagora il quadrato costruito sull’ipotenusa
4 volte il quadrato costruito sul cateto minore, è possibile trovare il lato
del quadrato costruito sul cateto minore sapendo che questo quadrato
ha area pari a un terzo di quella costruita sull’altro cateto …
𝐴𝐵 =
𝐴𝐶
𝐴𝐶 2
(2√3)2
4∙3
= 𝑐1 = √
=√
=√
= 2 𝑐𝑚
2
3
3
3
𝐵𝐶 = 𝑖 = 2 ∙ 𝐴𝐵 = 2 ∙ 𝑐1 = 2 ∙ 2 = 4 𝑐𝑚
𝐴=
𝑏 ∙ ℎ 𝐴𝐵 ∙ 𝐴𝐶 2 ∙ 4√3
=
=
= 4√3 𝑐𝑚2
2
2
2
2𝑝 = 𝐴𝐵 + 𝐵𝐶 + 𝐴𝐶 = 2 + 4 + 2√3 = (6 + 2√3 ) 𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 16
Un triangolo rettangolo ABC, rettangolo in A, ha i due angoli acuti
uguali e la sua ipotenusa BC misura 6√2 cm. Calcola il perimetro e
l’area del triangolo.
Dati e relazioni
𝐴̂ = 90°
𝐵̂ = 𝐶̂
𝐵𝐶 = 6√2 𝑐𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝;
2. 𝐴𝑟𝑒𝑎
Il triangolo rettangolo ha due angoli di 45° [(180°-90°)/2=45°] ed è
quindi isoscele e come tale ha due lati uguali
Essendo per il Teorema di Pitagora il quadrato costruito sull’ipotenusa
somma di due quadrati uguali costruiti sui cateti, è possibile trovare il
lato di uno dei quadrati costruiti sui cateti …
𝐴𝐵 = 𝐴𝐶 = 𝑐1 = 𝑐2 = √
𝐴=
𝐶𝐵 2 √(6√2)2
64 ∙ 2
=
=√
= 8 𝑐𝑚
2
2
2
𝑏 ∙ ℎ 𝐴𝐵 ∙ 𝐴𝐶 8 ∙ 8
=
=
= 32 𝑐𝑚2
2
2
2
2𝑝 = 𝐴𝐵 + 𝐵𝐶 + 𝐴𝐶 = 8 + 8 + 6√2 = (16 + 6√2 ) 𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 17
Un triangolo rettangolo ABC, rettangolo in A, ha l’angolo in B che il
doppio dell’angolo in C e il cateto maggiore AC che misura 6√3 cm.
Calcola il perimetro e l’area del triangolo.
Dati e relazioni
𝐴̂ = 90°
𝐵̂ = 2 ∙ 𝐶̂
𝐵𝐶 = 6√3 𝑐𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝; 2. 𝐴𝑟𝑒𝑎
180° − 𝐴̂ (180 − 90) 90
=
=
= 30°
3
3
3
𝐵̂ = 2 ∙ 𝐶̂ = 2 ∙ 30° = 60°
𝐶̂ =
Un triangolo rettangolo che ha due angoli di 30° e di 60° è la metà di un
triangolo equilatero. Il lato maggiore, l’ipotenusa, è quindi il doppio del
cateto minore.
Essendo per il Teorema di Pitagora il quadrato costruito sull’ipotenusa 4
volte il quadrato costruito sul cateto minore, è possibile trovare il lato del
quadrato costruito sul cateto minore sapendo che questo quadrato ha
area pari a un terzo di quella costruita sull’altro cateto …
𝐴𝐶
𝐴𝐶 2
(6√3)2
36 ∙ 3
√
√
𝐴𝐵 =
= 𝑐1 =
=
=√
= 6 𝑐𝑚
2
3
3
3
𝐵𝐶 = 𝑖 = 2 ∙ 𝐴𝐵 = 2 ∙ 𝑐1 = 2 ∙ 6 = 12 𝑐𝑚
𝐴=
𝑏 ∙ ℎ 𝐴𝐵 ∙ 𝐴𝐶 6 ∙ 6√3
=
=
= 18√3 𝑐𝑚2
2
2
2
2𝑝 = 𝐴𝐵 + 𝐵𝐶 + 𝐴𝐶 = 6 + 12 + 6√3 = (18 + 6√3 ) 𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 18
Un triangolo rettangolo ABC, rettangolo in A, ha i due angoli acuti da 45°
e la sua ipotenusa BC misura 6√2 cm. Calcola il perimetro e l’area del
triangolo.
Dati e relazioni
𝐴̂ = 90°
𝐵̂ = 𝐶̂ = 45°
𝐵𝐶 = 6√2 𝑐𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝; 2. 𝐴𝑟𝑒𝑎
Il triangolo rettangolo è isoscele avendo due angoli di 45°.
Essendo per il Teorema di Pitagora il quadrato costruito sull’ipotenusa
somma di due quadrati uguali costruiti sui cateti, è possibile trovare il
lato di uno dei quadrati costruiti sui cateti …
𝐴𝐵 = 𝐴𝐶 = 𝑐1 = 𝑐2 = √
𝐴=
𝐶𝐵 2 √(6√2)2
36 ∙ 2
=
=√
= 6 𝑐𝑚
2
2
2
𝑏 ∙ ℎ 𝐴𝐵 ∙ 𝐴𝐶 6 ∙ 6
=
=
= 18 𝑐𝑚2
2
2
2
2𝑝 = 𝐴𝐵 + 𝐵𝐶 + 𝐴𝐶 = 6 + 6 + 6√2 = (12 + 6√2 ) 𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 19
Un triangolo rettangolo ABC, rettangolo in A, è isoscele e il suo cateto AB
misura 12 cm. Calcola il perimetro e l’area del triangolo.
Dati e relazioni
𝐴̂ = 90°
𝐴𝐵 = 𝐴𝐶
𝐴𝐵 = 12 𝑐𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝; 2. 𝐴𝑟𝑒𝑎
𝐴𝐵 = 𝐴𝐶 = 𝑐1 = 𝑐2 = 12 𝑐𝑚
𝐵𝐶 = 𝑖 = √𝐴𝐵 2 + 𝐴𝐶 2
𝐵𝐶 = √122 + 122 = √144 + 144 = √144 ∙ 2 = 12√2 𝑐𝑚
𝐴=
𝑏 ∙ ℎ 𝐴𝐵 ∙ 𝐴𝐶 12 ∙ 12
=
=
= 72 𝑐𝑚2
2
2
2
2𝑝 = 𝐴𝐵 + 𝐵𝐶 + 𝐴𝐶 = 12 + 12 + 12√2 = (24 + 12√2 ) 𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 20
In un triangolo ABC l’altezza CH, lunga 24 cm, forma con il lato AC un
angolo di 60° e con il lato BC un angolo di 45°. Calcolate il perimetro e
l’area del triangolo dato.
Dati e relazioni
𝐶𝐻 = 24 𝑐𝑚
𝐴𝐶̂ 𝐻 = 60°
𝐵𝐶̂ 𝐻 = 45°
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝; 2. 𝐴𝑟𝑒𝑎
̂ + 𝐵𝐶̂ 𝐻) = 180° − (90° + 60°) = 30°
𝐵̂ = 180° − (𝐻
Un triangolo rettangolo con due angoli di 45° è isoscele.
Per costruzione, quindi, si ha CH = HB = 24 cm
̂ + 𝐵𝐶̂ 𝐻) = 180° − (90° + 60°) = 30°
𝐴̂ = 180° − (𝐻
Un triangolo rettangolo che ha due angoli di 30° e di 60° è la metà di un
triangolo equilatero. Il lato maggiore, l’ipotenusa, è quindi il doppio del
cateto minore.
𝐴𝐶 = 2 ∙ 𝐶𝐻 = 2 ∙ 24 = 48 𝑐𝑚
𝐶𝐵 = √𝐶𝐻 2 + 𝐻𝐵 2 = √242 + 242 = √2 ∙ 242 = 24√2 𝑐𝑚
𝐶𝐵 = 24√2 𝑐𝑚 ≅ 33,94 𝑐𝑚
𝐴𝐻 = √𝐴𝐶 2 − 𝐶𝐻 2 = √482 − 242 = √2304 − 576 = √1728
= 24√3 𝑐𝑚
𝐴𝐻 = 24√3 𝑐𝑚 ≈ 41,56 𝑐𝑚
𝐴𝐵 = 𝐴𝐻 + 𝐻𝐵 = 41,56 + 24 = 65,56 𝑐𝑚
2𝑝 = 𝐴𝐵 + 𝐵𝐶 + 𝐴𝐶 = 65,56 + 33,94 + 48 = 147,50 𝑐𝑚
𝐴=
𝑏 ∙ ℎ 41,56 ∙ 24
=
= 498,72 𝑐𝑚2
2
2
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 21
In un triangolo isoscele ABC l’angolo al vertice è di 120° e uno dei lati
uguali misura 4 m. Calcolate il perimetro e l’area del triangolo dato.
Dati e relazioni
𝐴𝐵𝐶 è 𝑖𝑠𝑜𝑠𝑐𝑒𝑙𝑒
𝐴𝐵 = 𝐴𝐶 = 4 𝑚
𝐴̂ = 120°
𝐵𝐶 = 6√2 𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝; 2. 𝐴𝑟𝑒𝑎
𝐴𝐻 =
𝐴𝐵 4
= = 2𝑚
2
2
𝐻𝐵 = 𝐻𝐶 = √𝐴𝐻 2 − 𝐴𝐻 2 = √42 − 22 = √16 − 4 = √12 = 2√3 𝑚
𝐻𝐵 = 𝐻𝐶 = 2√3 ≅ 3,46 𝑚
𝐵𝐶 = 2 ∙ 𝐵𝐻 = 2 ∙ 2√3 = 4 ∙ √3 ≈ 6,92 𝑚
Per costruzione
AB = AC = 4 m
2𝑝 = 2 ∙ 𝐴𝐵 + 𝐵𝐶 = 2 ∙ 4 + 6,92 = 8 + 6,92 ≈ 14,92 𝑚
𝐴=
𝑏 ∙ ℎ 4√3 ∙ 2
=
= 4√3 𝑚2
2
2
𝐴=
𝑏 ∙ ℎ 4√3 ∙ 2 6,92 ∙ 2
=
≅
≅ 6,92 𝑚2
2
2
2
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 22
Un trapezio isoscele ha i due angoli acuti alla base di 60°. Sapendo che la
base maggiore misura 16 m e la minore 10 m calcola il perimetro e l’area
del trapezio dato.
Dati e relazioni
𝑇𝑟𝑎𝑝𝑒𝑧𝑖𝑜 𝑖𝑠𝑜𝑠𝑐𝑒𝑙𝑒
𝐴̂ = 𝐵̂ = 60°
𝐴𝐵 = 16 𝑚
𝐶𝐷 = 10 𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝; 2. 𝐴𝑟𝑒𝑎
Un triangolo rettangolo
che ha due angoli di 30°
[(180°-(90°+60°)=30°]
e di 60° è la metà di un
triangolo equilatero. Il
lato maggiore,
l’ipotenusa, è quindi il
doppio del cateto
minore.
𝐴𝐵 − 𝐶𝐷 16 − 10 6
=
= = 3𝑚
2
2
2
𝐴𝐷 = 2𝐴𝐻 = 2 ∙ 𝐴𝐻 = 2 ∙ 3 = 6 𝑚
𝐴𝐻 =
𝐷𝐻 = √𝐴𝐷2 − 𝐴𝐻 2 = √62 − 32 = √36 − 9 = √27 = √9 ∙ 3 = 3√3 𝑚
𝐴=
𝐴𝐵 + 𝐶𝐷
16 + 10
∙ 𝐷𝐻 =
∙ 3√3 = 13 ∙ 3√3 = 39√3 𝑚2
2
2
2𝑝 = 𝐴𝐵 + 𝐷𝐶 + 2𝐴𝐷 = 16 + 10 + 2 ∙ 3√3 = (26 + 6√3 ) 𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 23
Un trapezio isoscele ha i due angoli acuti alla base di 30°. Sapendo che
la base minore misura 20 cm e il lato obliquo 40 cm calcola il
perimetro e l’area del trapezio dato.
Dati e relazioni
𝑇𝑟𝑎𝑝𝑒𝑧𝑖𝑜 𝑖𝑠𝑜𝑠𝑐𝑒𝑙𝑒 𝐴𝐵𝐶𝐷
𝐴̂ = 𝐵̂ = 30°
𝐶𝐷 = 𝑙 = 40 𝑐𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝;
2. 𝐴𝑟𝑒𝑎
Il triangolo rettangolo
AHD è la metà di un
triangolo equilatero
perché ha gli angoli acuti
di 30° e 60° e il lato
maggiore AD,
l’ipotenusa, che è il
doppio del cateto minore
DH.
𝐴𝐷 = 40 𝑐𝑚
𝐷𝐻 =
𝐴𝐷 40
=
= 20 𝑐𝑚
2
2
𝐴𝐻 = √𝐴𝐷2 − 𝐷𝐻 2
𝐴𝐻 = √402 − 202 = √1600 − 400 = √1200 = √400 ∙ 3
= 20√3 𝑐𝑚
𝐴𝐵 = 𝐷𝐶 + 2𝐴𝐻 = 20 + 2 ∙ 20√3 = (20 + 40√3) 𝑐𝑚
𝐴=
𝐴=
𝐴𝐵 + 𝐶𝐷
∙ 𝐷𝐻
2
20 + 40√3 + 20
∙ 20 = 10 ∙ (40 + 40√3)
2
= (400 + 400√3 ) 𝑐𝑚2
2𝑝 = 𝐴𝐵 + 𝐶𝐷 + 2𝐴𝐷
2𝑝 = 20 + 40√3 + 20 + 2 ∙ 40 = (120 + 40√3 ) 𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 24
Un trapezio isoscele ha i due angoli acuti alla base di 45°.
Sapendo che l’altezza del trapezio misura 12 cm e che la base
minore congruente a questa calcola il perimetro e l’area del
trapezio dato.
Dati e relazioni
𝑇𝑟𝑎𝑝𝑒𝑧𝑖𝑜 𝑖𝑠𝑜𝑠𝑐𝑒𝑙𝑒 𝐴𝐵𝐶𝐷
𝐴̂ = 𝐵̂ = 45°
𝐷𝐻 = ℎ = 12 𝑐𝑚
𝐷𝐻 = 𝐶𝐷
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝;
2. 𝐴𝑟𝑒𝑎
Il triangolo rettangolo
AHD è isoscele perché ha
gli angoli acuti di 45°.
Un triangolo rettangolo con due angoli di 45° è isoscele.
𝐴𝐻 = 𝐷𝐻 = 𝐶𝐷 = 12 𝑐𝑚
𝐴𝐷 = √𝐴𝐻 2 + 𝐷𝐻 2 = √2𝐴𝐻 2 = √2 ∙ 122 = √122 √2
= 12√2 𝑐𝑚
𝐴𝐵 = 𝐷𝐶 + 2𝐴𝐻 = 3 ∙ 12 = 36 𝑐𝑚
𝐴=
𝐴𝐵 + 𝐶𝐷
36 + 12
∙ 𝐷𝐻 =
∙ 12 = 6 ∙ 48 = 288 𝑐𝑚2
2
2
2𝑝 = 𝐴𝐵 + 𝐶𝐷 + 2𝐴𝐷 = 36 + 12 + 2 ∙ 12√2
= (48 + 24√2 ) 𝑐𝑚
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 25
Un trapezio isoscele ha i due angoli acuti alla base rispettivamente di 45°
e 30°. Sapendo che la base minore è un terzo della maggiore e che
l’altezza misura 6 cm calcola il perimetro e l’area del trapezio dato.
Dati e relazioni
𝑇𝑟𝑎𝑝𝑒𝑧𝑖𝑜 𝐴𝐵𝐶𝐷
𝐴̂ = 30°
𝐵̂ = 60°
ℎ = 6 𝑐𝑚
1
𝐶𝐷 = 𝐴𝐵
3
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝;
2. 𝐴𝑟𝑒𝑎
Il triangolo rettangolo
AHD è la metà di un
triangolo equilatero
perché ha gli angoli
acuti di 30° e 60° e il
lato maggiore AD,
l’ipotenusa, che è il
doppio del cateto
minore DH.
DA CONTROLLARE Liceo Giovanni
𝑏1 = 3 𝑏2
𝐴𝐷 = 2 ∙ 𝐷𝐻 = 2 ∙ 6 = 12 𝑐𝑚
𝑙 √3 12 ∙ √3
=
= 6 √3 𝑐𝑚
2
2
𝐶𝐸 = 𝐷𝐻 = 𝐸𝐵 = 6 𝑐𝑚
𝐴𝐻 =
𝐶𝐵 = 𝑙√2 = 6√2 𝑐𝑚
𝐶𝐷 = 𝑥
3𝑥 = 6 √3 + 𝑥 + 6
= (3 + √3)𝑐𝑚
2𝑥 = 6 √3 + 6 𝑥
𝐴𝐵 = 6√3 + 3 + 3√3 + 6 = (9 + 9√3) 𝑐𝑚
Il triangolo rettangolo
BEC è isoscele perché
ha gli angoli acuti di
45°.
2𝑝 = 𝐴𝐵 + 𝐵𝐶 + 𝐶𝐷 + 𝐴𝐷
2𝑝 = 9 + 9√3 + 6√2 + 3 + 3√3 + 12 = (24 + 12√3 + 6√2 ) 𝑐𝑚
𝐴=
9 + 9√3 + 3 + 3√3
∙ 6 = 3 ∙ (12 + 12 ∙ √3)
2
= (36 + 36 ∙ √3) 𝑐𝑚2
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 26
Un rombo è formato da due triangoli equilateri sovrapposti. Sapendo che il
perimetro del rombo misura 120 cm calcola l’area della figura.
Dati e relazioni
𝑅𝑜𝑚𝑏𝑜 𝐴𝐵𝐶
𝐴𝐵𝐶 è 𝑡. 𝑒𝑞𝑢𝑖𝑙𝑎𝑡𝑒𝑟𝑜
𝐴𝐵𝐷 è 𝑡. 𝑒𝑞𝑢𝑖𝑙𝑎𝑡𝑒𝑟𝑜
𝐴̂ = 𝐵̂ = 𝐶̂ = 60°
2𝑝 = 120 𝑐𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑎
𝐴𝑟𝑒𝑎
Il triangolo rettangolo AHC è la metà di un triangolo equilatero (ABC) per
costruzione. Il lato maggiore AC, l’ipotenusa, è quindi il doppio del cateto
minore AH.
𝐴𝐶 = 𝐶𝐵 = 𝐵𝐷 = 𝐴𝐷 = 𝐴𝐵 =
𝐴𝐻 =
2𝑝 120
=
= 30 𝑐𝑚
4
4
𝐴𝐶 30
=
= 15 𝑐𝑚
2
2
𝐶𝐻 = √𝐴𝐶 2 − 𝐴𝐻 2
𝐶𝐻 = √302 − 152 = √900 − 225 = √675 = √225 ∙ 3 = 15√3 𝑐𝑚
𝐶𝐷 = 2𝐶𝐻 = 2 ∙ 15√3 = 30√3 𝑐𝑚
𝐴=
𝐴𝐵 ∙ 𝐶𝐷 30 ∙ 30√3
=
= 15 ∙ 30√3 = 450√3 𝑐𝑚2
2
2
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 27
Un parallelogramma ha i due angoli acuti alla base di 60°. Sapendo
che i lati obliqui misurano 8 cm e le basi 9 cm calcolane il perimetro e
l’area.
Dati e relazioni
𝑃𝑎𝑟𝑎𝑙𝑙𝑒𝑙𝑜𝑔𝑟𝑎𝑚𝑚𝑎 𝐴𝐵𝐶𝐷
𝐴̂ = 𝐶̂ = 60°
𝐴𝐵 = 𝐶𝐷 = 9 𝑐𝑚
𝐴𝐷 = 𝐵𝐶 = 8 𝑐𝑚
𝑅𝑖𝑐ℎ𝑖𝑒𝑠𝑡𝑒
1. 2𝑝; 2. 𝐴𝑟𝑒𝑎
Il triangolo rettangolo
AHD è la metà di un
triangolo equilatero
perché ha gli angoli acuti
di 30° e 60° e il lato
maggiore AD, l’ipotenusa,
che è il doppio del cateto
minore AH.
𝐴𝐻 =
𝐴𝐷 8
= = 4 𝑐𝑚
2
2
𝐷𝐻 = √𝐴𝐷2 − 𝐴𝐻 2 = √82 − 42 = √64 − 16 = √48 = √16 ∙ 3
= 4√3 𝑐𝑚
𝐴𝐵 ∙ 𝐷𝐻 9 ∙ 4√3
=
= 18√3 𝑐𝑚2
2
2
2𝑝 = 2𝐴𝐵 + 2𝐴𝐷 = 2 ∙ 9 + 2 ∙ 8 = 18 + 16 = 34 𝑐𝑚
𝐴=
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 28
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale
Teorema di Pitagora. Triangoli con angoli di 45°, 30° e 60°. Eserciziario ragionato con soluzioni. - 29
Keywords
Geometria, Geometria piana, teorema di Pitagora, Pitagora, Equivalenza, Misura delle aree,
Area, Superficie, Triangolo, Triangolo isoscele, Triangolo rettangolo, Triangoli, Problemi di
geometria con soluzioni
Geometry, Pythagoras, Pythagoras’s theorem, Area, Area Measurement, Triangle,
Triangles, triangle equilateral, triangle isosceles, triangle scalene, Geometry Problems with
Solutions
Geometría, Área, Superficie, Perímetro y áreas de figures planes, triángulos, triángulo,
equilátero, isósceles, escaleno, Área figures planes
Géométrie, Pythagore, Théorème de Pythagore, Aire, Triangle, Isocèle, équilatéral, scalène,
Superficie, Aires et périmètres
Geometrie, Umfang, Fläche, Triangel, Dreieck, spitzwinkliges Dreieck, rechtwinkliges
Dreieck, stumpfwinkliges Dreieck, Satz des Pythagoras, Pythagoras, Dreiecksgeometrie, Satz,
Mathematik
Teorema de Pitàgores
Stelling van Pythagoras
Pisagor teoremi
Πυθαγόρειο θεώρημα
Den pythagoræiske læresætning
Teorema de Pitágoras
Pythagoras’ læresetning
Pythagoras sats
Pythagoraan lause
Теорема Піфагора
Pythagorova věta
Twierdzenie Pitagorasa
Teorema lui Pitagora
‫فيثاغورس مبرهنة‬
勾股定理
ピタゴラスの定理
Copyright© 1987-2017 owned by Ubaldo Pernigo, www-ubimath.org - contact: [email protected]
Il presente lavoro è coperto da Licenza Creative Commons Attribuzione - Non commerciale - Non opere derivate 4.0 Internazionale