4
Capitolo
Semplificazioni di schemi a blocchi
4.1
Blocchi in cascata
4.2
Blocchi in parallelo
4.3
Blocchi in catena chiusa (reazione negativa)
4.4
Blocchi in catena chiusa (reazione positiva)
4.5
Spostamento di blocchi
4.6
Esercizi
Algebra degli schemi a blocchi
ALGEBRA DEGLI SCHEMI A BLOCCHI
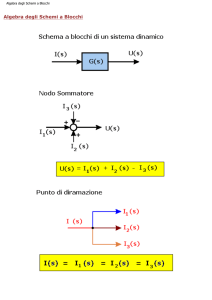
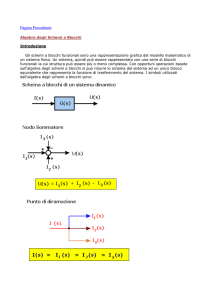
L’algebra degli schemi a blocchi è un insieme di operazioni che permettono di semplificare
schemi complessi
4.1
BLOCCHI IN CASCATA
Due blocchi sono connessi in cascata quando l’uscita del primo è il segnale d’ingresso del
secondo.
La funzione di trasferimento di più blocchi in cascata è data dal prodotto delle funzioni di
trasferimento dei singoli blocchi.
Nel nostro caso G (s ) = G1(s ) ⋅ G 2(s )
Dimostrazione che G (s ) = G1(s ) ⋅ G 2(s )
U1(s )
f.d.t. del primo blocco
E(s)
U(s )
f.d.t. del secondo blocco
G2(s ) =
U1(s)
U(s )
f.d.t. del sistema
G (s ) =
E(s)
G1(s ) =
G (s ) =
U(s ) U1(s ) U(s )
=
⋅
= G1(s ) ⋅ G 2(s )
E(s) E(s ) U1(s )
Prof. Francesco Di Sabatino - Dispense di Sistemi Elettronici Automatici
IV-2
Algebra degli schemi a blocchi
4.2
BLOCCHI IN PARALLELO
Due blocchi sono connessi in parallelo quando ricevono lo stesso segnale d’ingresso e le loro
uscite sono sommate
nodo
sommatore
La funzione di trasferimento di più blocchi in parallelo è data dalla somma delle funzioni di
trasferimento dei singoli blocchi
Nel nostro caso: G (s ) = G1(s ) + G 2(s)
Dimostrazione che
G1(s ) =
G (s ) =
U1(s )
E(s)
G (s ) = G1(s ) + G 2(s)
; G2(s ) =
U2(s )
;
E(s)
G (s ) =
U(s )
E(s)
U(s ) U1(s ) + U 2(s ) U1(s ) U 2(s )
=
=
+
= G1(s ) + G 2(s)
E(s)
E(s )
E(s )
E(s )
Prof. Francesco Di Sabatino - Dispense di Sistemi Elettronici Automatici
IV-3
Algebra degli schemi a blocchi
4.3
BLOCCHI IN CATENA CHIUSA (reazione negativa)
Lo schema di un sistema a catena chiusa in reazione negativa è il seguente:
In questo sistema il nodo sommatore effettua la differenza tra il segnale d’ingresso e quello di
reazione.
W (s ) =
U(s )
E(s)
f.d.t. ad anello chiuso
L(s) = G(S)·H(S)
U(s) = G(s)·ε(s)
H(s ) =
R (s )
U(s )
f.d.t. del blocco di reazione
f.d.t. ad anello aperto
Dimostrazione che W (s ) =
dove:
;
G (s )
1 + G (s )H(s )
[1]
ε(s) = E(s ) − R (s ) = E(s ) − H(s )U(s )
[2]
U(s ) = G (s ) ⋅ [E(s ) − H(s )U(s )]
sostituendo la [2] nella [1] si ottiene
risolvendo rispetto ad U(s) si ottiene:
U(s ) = G (s )E(s ) − G (s )H(s )U(s )
U(s ) =
⇒
U(s ) ⋅ [1 + G (s )H(s )] = G (s)E(s)
G (s )E(s )
1 + G (s )H(s )
dividendo entrambi i membri per E(s) si ricava la W (s ) :
W (s ) =
U(s )
G (s )
=
E(s )
1 + G (s )H(s )
c.v.d.
Prof. Francesco Di Sabatino - Dispense di Sistemi Elettronici Automatici
IV-4
Algebra degli schemi a blocchi
4.4
BLOCCHI IN CATENA CHIUSA (reazione positiva)
Lo schema di un sistema a catena chiusa in reazione positiva è il seguente:
In questo sistema il nodo sommatore effettua la somma tra il segnale d’ingresso e quello di
reazione.
Dimostrazione che W (s ) =
U(s) = G(s)·ε(s)
dove:
G (s )
1 − G (s )H(s )
[1]
ε(s) = E(s ) + R (s ) = E(s ) + H(s )U(s )
[2]
U(s ) = G (s ) ⋅ [E(s ) + H(s )U(s )]
sostituendo la [2] nella [1] si ottiene
risolvendo rispetto ad U(s) si ottiene:
U(s ) = G (s )E(s ) + G (s )H(s )U(s )
U(s ) =
⇒
U(s ) ⋅ [1 − G (s )H(s )] = G (s)E(s)
G (s )E(s )
1 − G (s )H(s )
dividendo entrambi i membri per E(s) si ricava la W (s ) :
W (s ) =
G (s )
U(s )
=
E(s )
1 − G (s )H(s )
c.v.d.
Prof. Francesco Di Sabatino - Dispense di Sistemi Elettronici Automatici
IV-5
Algebra degli schemi a blocchi
1
Prof. Francesco Di Sabatino - Dispense di Sistemi Elettronici Automatici
IV-6
Algebra degli schemi a blocchi
1
1
VI-16 Manuale di Elettronica e Telecomunicazioni - Hoepli
Prof. Francesco Di Sabatino - Dispense di Sistemi Elettronici Automatici
IV-7
Algebra degli schemi a blocchi
4.6
ESERCIZI
Esercizio 1
Determinare la f.d.t. ad anello chiuso
Il circuito retroazionato è equivalente al circuito in figura
G (s) =
5
s+2
e
H(s)=1
sostituendo:
5
W (s ) = s + 2 =
5
1+
s+2
5
5
s+2
=
s+2+5
s+7
s+2
Esercizio 2
Determinare la f.d.t. ad anello chiuso
Il circuito equivalente e:
Prof. Francesco Di Sabatino - Dispense di Sistemi Elettronici Automatici
IV-8
Algebra degli schemi a blocchi
L(s) = G(s)·H(s )=
10
5
50
· =
(s + 2)(s + 3) s s(s + 2)(s + 3)
(f.d.t. ad anello aperto)
sostituendo:
10
10s
10s
(s + 2)(s + 3)
W (s ) =
=
=
3
2
50
s(s + 2)(s + 3) + 50 s + 5s + 6s + 50
1+
s(s + 2)(s + 3)
Esercizio 3
Uno stabilimento utilizza, per la cottura di merendine, un sistema di controllo di temperatura a
catena chiusa. Sapendo che le funzioni di trasferimento del regolatore, del circuito di comando,
del forno e del circuito di reazione(termocoppia e circuito di condizionamento) sono
rispettivamente:
G K (s) = 0,1
G A (s) = 3
G F (s) =
0,2
1 + 500s
G R (s) =
0,125
1 + 50s
Determinare la f.d.t. complessiva del sistema
Soluzione
Il circuito equivalente e:
G(s) = 0,1 ⋅ 3 ⋅
0,2
0,06
=
1 + 500s 1 + 500s
L(s) = G(s) ⋅H(s) =
; H(s) =
0,125
1 + 50s
0,06
0,0075
0,125
=
⋅
1 + 500s 1 + 50s
(1 + 50s) ⋅ (1 + 500s)
Prof. Francesco Di Sabatino - Dispense di Sistemi Elettronici Automatici
IV-9
Algebra degli schemi a blocchi
sostituendo:
0,06
0,06
1 + 500s
1 + 500s
W(s ) =
=
=
0,0075
(1 + 50s) ⋅ (1 + 500s) + 0,0075
1+
(1 + 50s) ⋅ (1 + 500s)
(1 + 50s) ⋅ (1 + 500s)
=
0,06 ⋅ (1 + 50s)
0,06 ⋅ (1 + 50s)
≅
(1 + 50s) ⋅ (1 + 500s) + 0,0075 25000s 2 + 550s + 1
Esercizio 4
Ricavare la f.d.t. del sistema
1° Metodo
Nel nodo d’ingresso
⇒
A=E-B-C
E=A+B+C
[1]
Calcolo di C in funzione di U
C = s⋅U
Calcolo di B in funzione di U
U = 5 ⋅B
⇒ B=
1
U
5
Calcolo di A in funzione di U
B=
s +1
2
A ⇒ A=
B
2
s +1
⇒ A=
s +1 1
s +1
⋅ U ⇒ A=
U
2 5
10
Sostituendo nella [1] si ha:
s +1
1
s + 1 1
U + U + s⋅U
⇒ E=
+ + s ⋅U ⇒
10
5
10 5
11s + 3
10
E=
U
⇒
U=
E
10
11s + 3
E=
Dalla quale si ottiene:
W(s) =
U(s)
10
=
E (s)
11s + 3
2° Metodo
Prof. Francesco Di Sabatino - Dispense di Sistemi Elettronici Automatici
IV-10
Algebra degli schemi a blocchi
2
2
F(s) = s + 1 =
2
s+3
1+
s +1
G(s) = 5⋅F(s) =
10
s+3
G(s) ⋅H(s) =
e
G (s)
W(s) =
=
1 + G (s) ⋅ H(s)
10
10s
⋅s =
s+3
s+3
10
s + 3 = 10
10s
11s + 3
1+
s+3
Esercizio 5
Ricavare la f.d.t. del sistema.
A=
1
[E − B] [1]
s+2
B = 4⋅A + U
[2]
sostituendo la [2] nella [1]
Prof. Francesco Di Sabatino - Dispense di Sistemi Elettronici Automatici
IV-11
Algebra degli schemi a blocchi
1
[E − 4A − U ]
s+2
A=
ricavo A
U=
[3]
in Funzione di U
1
A
s+3
⇒
A = (s + 3) ⋅ U
[4]
sostituendo la [4] nella [3]
(s + 3) ⋅ U =
1
[E − 4(s + 3) ⋅ U − U]
s+2
(s + 3) ⋅ U =
1
4(s + 3)
1
E −
U−
U
s+2
s+2
s+2
(s + 3) ⋅ U(s) +
4(s + 3)
1
1
U+
U =
E
s+2
s+2
s+2
[(s + 3)(s + 2) + 4(s + 3) + 1] ⋅ U =E
(s 2 + 9s + 19)⋅ U = E
dalla quale si ottiene:
W(s) =
1
U(s)
=
E (s)
s 2 + 9s + 19
Esercizio 6
Ricondurre ad uno schema a reazione unitaria
Il circuito equivalente e:
sostituendo:
Prof. Francesco Di Sabatino - Dispense di Sistemi Elettronici Automatici
IV-12
Algebra degli schemi a blocchi
10
10s
10s
(s + 2)(s + 3)
W (s ) =
=
=
50
s(s + 2)(s + 3) + 50 s 3 + 5s 2 + 6s + 50
1+
s(s + 2)(s + 3)
Lo schema a reazione unitario è:
W(s) =
F(s)
1 + F(s)
uguagliando si ricava F(s)
10s
F(s)
=
3
1 + F(s) s + 5s 2 + 6s + 50
F(s) ⋅ (s 3 + 5s 2 + 6s + 50) = 10s ⋅ (1 + F(s))
F(s) ⋅ (s 3 + 5s 2 + 6s + 50) − 10s ⋅ F(s) = 10s
F(s) ⋅ (s 3 + 5s 2 + 6s + 50 − 10s) = 10s
10s
F(s) =
s 3 + 5s 2 − 4s + 50
Esercizio 7.
Determinare la f.d.t. del blocco di reazione
W (s) =
U(s)
10
=
E(s) s 2 + 2s + 10
Prof. Francesco Di Sabatino - Dispense di Sistemi Elettronici Automatici
IV-13
Algebra degli schemi a blocchi
Il circuito equivalente è:
uguagliando si ricava H(s)
10
G (s)
=
1 + G (s)H(s) s 2 + 2s + 10
10
10
s(s + 2)
=
⇒
2
10
s
+
2
s
+
10
1+
H(s)
s(s + 2)
10
2
s + 2s + 10 ⋅ H(s)
=
10
10
=
s(s + 2) + 10 ⋅ H (s) s 2 + 2s + 10
10
2
s + 2s + 10
consegue
H(s)=1
Prof. Francesco Di Sabatino - Dispense di Sistemi Elettronici Automatici
IV-14
Algebra degli schemi a blocchi
Esercizio 8
Determinare l’uscita del sistema ad anello chiuso in presenza del disturbo ∆1(s)
Soluzione
Per determinare l’uscita applichiamo il principio di sovrapposizione degli effetti.
•
Consideriamo agente solo il segnale R(s) indi poniamo ∆1(s) =0
Riducendo i due blocchi in cascata ad un solo blocco si ha:
W1 =
U1
G1 ⋅ G 2
=
R 1 + G1 ⋅ G 2 ⋅ H
8
8
(s + 1)(s + 2)(s + 3)
=
=
W1 (s) =
32
(s + 1)(s + 2)(s + 3) + 32
1+
(s + 1)(s + 2)(s + 3)
8
8
(s 2 + 3s + 2)(s + 3) + 8
=
(s 2 + 3s + 2)(s + 3) + 32
dalla quale si ottiene:
W 1 (s ) =
8
s 3 + 6s 2 + 11s + 38
U1 (s) = R (s) ⋅
(f.d.t. del sistema in assenza del disturbo)
8
s 3 + 6s 2 + 11s + 38
(uscita complessa in assenza del disturbo)
Prof. Francesco Di Sabatino - Dispense di Sistemi Elettronici Automatici
IV-15
Algebra degli schemi a blocchi
•
Consideriamo ora, agente solo il disturbo ∆1(s), indi poniamo R(s) = 0
Nota: il blocco –1 è dovuto al nodo sommatore che ora svolge la funzione invertente
Lo schema è equivalente è:
Riducendo i due blocchi in cascata ad un solo blocco si ha
W2 =
U2
G2
=
∆1 1 + G 2 ⋅ G 1 ⋅ H
8
8
8(s + 3)
(s + 1)(s + 2)
(s + 1)(s + 2)
=
=
W2 =
32
(s + 1)(+2)(s + 3) + 32 (s + 1)(s + 2)(s + 3)
1+
(s + 1)(s + 2)(s + 3)
(s + 1)(s + 2)(s + 3)
dalla quale si ottiene
W 2 (s)=
U 2 (s)
∆1 (s)
U 2 (s) = ∆1 (s) ⋅
=
8(s + 3)
s 3 + +6s 2 + 11s + 38
8(s + 3)
s 3 + 6s 2 + 11s + 38
U(s) = U1 (s) + U 2 (s)
( f.d.t. del disturbo)
(uscita complessa dovuta al solo disturbo)
( risposta complessa del sistema)
Prof. Francesco Di Sabatino - Dispense di Sistemi Elettronici Automatici
IV-16