TEORIA dei CIRCUITI
Ingegneria dell’Informazione
− TRANSITORI−
Stefano Pastore
Dipartimento di Ingegneria e Architettura
Corso di Teoria dei Circuiti (105IN)
a.a. 2013-14
Introduzione
•
•
•
•
Studieremo il transitorio nel dominio del
tempo dei circuiti LDI
Come transitorio intendiamo l’evoluzione
dinamica del circuito da uno stato prefissato,
dovuto alle condizioni iniziali dei
componenti dinamici, allo stato di regime,
dovuto alle sorgenti indipendenti
L’ordine del circuito è dato dal numero di
elementi dinamici indipendenti presenti nel
circuito. Come “indipendenti” si intende che
non ci sono relazioni lineari che legano tra
loro le variabili di stato. In tal caso il
circuito è detto degenere
Ci concentreremo sui circuiti del I ordine,
con condensatore o induttore. Accenneremo
alla soluzione dei circuiti di II ordine e di
ordine superiore
2
Equazione differenziale del I ordine
• Consideriamo la seguente equazione
differenziale del I ordine lineare a
coefficienti costanti con condizione
iniziale X0
x(t ) xs (t )
x& (t ) = −
+
τ
τ
x(0) = X 0
• La soluzione generale di questa
equazione differenziale è costituita da
una famiglia di funzioni x(t). Si può
dimostrare che esiste una sola
soluzione di questa famiglia che ha
come condizione iniziale X0
3
Equazione omogenea associata
• Definiamo come “omogenea associata”
l’equazione differenziale ottenuta ponendo a
zero il termine noto xs(t) (forzante), ovvero
x& (t ) = −
o
o
x (t )
τ
• La soluzione dell’omogenea associata è:
x o (t ) = K e
−
t
τ
• La differenza di due soluzioni è ancora
soluzione della omogenea associata
−
t
x10 (t ) = K1 e τ ,
x20 (t ) = K 2 e
−
t
τ
K '4
647
8 −t
0
0
⇒ x1 (t ) − x2 (t ) = (K1 − K 2 )e τ
4
Differenza di soluzioni
• Supponiamo che x1(t) e x2(t) siano due
soluzioni generali della famiglia, allora la loro
differenza sarà comunque soluzione
dell’omogenea associata
x&1 (t ) = −
x1 (t )
x&2 (t ) = −
x 2 (t )
τ
τ
+
x s (t )
+
x s (t )
τ
τ
(
d
x1 (t ) − x2 (t ))
(x1 (t ) − x2 (t ) ) = −
dt
τ
• Quindi
x1 (t ) − x2 (t ) = x (t ) = K 'e
o
−
t
τ
5
Soluzione generale
• La soluzione generale dell’equazione
differenziale sarà data dalla soluzione
dell’omogenea associata sommata a una
soluzione qualsiasi, detta particolare, della
equazione completa
x(t ) = Ke
−
t
τ
+ x (t )
p
• Infatti si ha
−
t
x1 (t ) − x2 (t ) = K1e τ + x p (t ) −
t
−
p
τ
− K 2 e + x (t ) =
= (K1 − K 2 )e
−
t
τ
= K 'e
−
t
τ
6
Soluzione generale (2)
• La costante K viene determinata
imponendo la condizione iniziale,
ovvero:
x ( 0) = X 0 = K + x p ( 0)
⇒ K = X 0 − x p (0)
• Da cui la soluzione generale per t ≥ 0
con condizione iniziale X0 è
(
)
x(t ) = X 0 − x p (0) e
t≥0
−
t
τ
+ x p (t )
7
Soluzione generale omogenea
• Se l’equazione differenziale non
contiene termine forzante, la soluzione
generale con condizione iniziale X0 è:
x(t ) = X 0 e
−
t
τ
• Questo caso corrisponde, come
vedremo, alla scarica di un
condensatore o di un induttore su una
resistenza
8
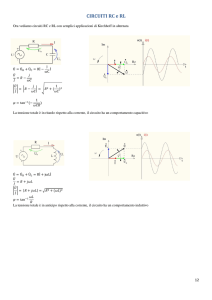
Circuiti RC del I ordine
• Possiamo applicare alla parte resistiva di un
circuito LDI RC del I ordine (ai morsetti del
condensatore) il teorema di Thevenin
• Quindi questo semplice circuito RC riassume
il comportamento di tutti i circuiti LDI RC del
I ordine
• Prima troveremo vC(t), poi vedremo come
determinare le altre variabili del circuito
9
Equazione differenziale
• Scriviamo l’equazione differenziale del
circuito per t ≥ 0 e vC(0) = V0
veq (t ) = Req i (t ) + vC (t )
dvC (t )
i (t ) = C
dt
dvC (t )
→ veq (t ) = Req C
+ vC (t )
dt
• Definendo la “costante di tempo” come
τC = ReqC [s]
• Si ottiene per t ≥ 0
vC (t ) veq (t )
+
v&C (t ) = −
τC
τC
v (0) = V
0
C
10
Equazione omogenea
• Se il circuito è omogeneo e non ci sono
sorgenti indipendenti (veq(t) = 0), allora
l’equazione differenziale diventa
v&C (t ) = −
vC (t )
τC
• La soluzione rappresenta la scarica di
un condensatore su una resistenza con
condizione iniziale V0
vC (t ) = V0 e
−
t
τC
11
Soluzione generale
• Nel caso in cui ci siano delle sorgenti
indipendenti attive, la soluzione
generale con condizione iniziale V0 è
(
)
vC (t ) = V0 − vCp (0) e
−
t
τC
+ vCp (t ) V
t≥0
• Dove la soluzione particolare vpC(t)
dipende dal tipo di sorgente
12
Circuiti RL del I ordine
• Possiamo applicare alla parte resistiva di un
circuito LDI RL del I ordine (ai morsetti
dell’induttore) il teorema di Norton
• Quindi questo semplice circuito RL riassume
il comportamento di tutti i circuiti LDI RL del
I ordine
• Prima troveremo iL(t), poi vedremo come
determinare le altre variabili del circuito
13
Equazione differenziale
• Scriviamo l’equazione differenziale del
circuito per t ≥ 0 e iL(0) = I0
ieq (t ) = Geq v(t ) + iL (t )
diL (t )
v(t ) = L
dt
diL (t )
→ ieq (t ) = Geq L
+ iL (t )
dt
• Definendo la “costante di tempo” come
τL = GeqL [s]
• Si ottiene per t ≥ 0
&
iL (t ) ieq (t )
+
iL (t ) = −
τL
τL
i (0) = I
0
L
14
Equazione omogenea
• Se il circuito è omogeneo e non ci sono
sorgenti indipendenti (ieq(t) = 0), allora
l’equazione differenziale diventa
&iL (t ) = − iL (t )
τL
• La soluzione rappresenta la scarica di
un induttore su una resistenza con
condizione iniziale I0
iL (t ) = I 0 e
−
t
τL
15
Soluzione generale
• Nel caso in cui ci siano delle sorgenti
indipendenti attive, la soluzione
generale con condizione iniziale I0 è
(
)
iL (t ) = I 0 − iLp (0) e
−
t
τL
+ iLp (t ) A
t≥0
• Dove la soluzione particolare ipL(t)
dipende dal tipo di sorgente
16
Concetto di stabilità
• La soluzione dell’omogenea associata è detta
anche soluzione libera del circuito, in quanto
dipende solo dalle condizioni iniziali
• Un circuito con le sorgenti indipendenti poste
a zero è “stabile” se la soluzione libera tende
a zero per t ∞
• Essendo la soluzione libera uguale a
x oa (t ) = X 0 e
−
t
τ
“stabile” τ > 0
• Un circuito si dice invece instabile se: τ < 0,
quindi la soluzione xoa(t) ∞
• In un circuito stabile, l’energia
immagazzinata nel circuito viene dissipata
fino ad annullarsi per t ∞
• I circuiti che esamineremo saranno stabili
17
Stabilità nei circuiti nonlineari
• Consideriamo il seguente circuito
• La caratteristica del bipolo NRI è
18
Stabilità nei circuiti nonlineari (2)
• L’ equazione di stato del circuito è
1
i = g (v)
i = −Cv&(t ) → v&(t ) = − g (v) = f (v)
C
• La tensione e la corrente del
condensatore sono vincolati alla
caratteristica del bipolo, detta dynamic
route. I tre punti di equilibrio v1, v2 e v3
si ottengono ponendo:
v&(t ) = 0 → g (v) = 0
(i = 0)
• Corrispondono con le intersezioni della
caratteristica g(v) con l’asse delle
ascisse
19
Stabilità nei circuiti nonlineari (3)
• Facendo riferimento all’equazione nonnormale del condensatore, si possono
distinguere sulla dynamic route due
diversi andamenti della soluzione
semipiano superiore : i > 0 → v& < 0
semipiano inferiore : i < 0 → v& > 0
• Partendo da una qualsiasi condizione
iniziale v0, la soluzione seguirà il verso
delle frecce, come disegnato in figura
• Risulta quindi che la soluzione andrà
sempre verso uno dei due punti di
equilibrio di ascissa v1 e v3, mentre si
allontanerà dal punto v2
• Diciamo allora che i punti di equilibrio
v1 e v3 sono stabili, mentre il punto v2 è
instabile
20
Stabilità nei circuiti nonlineari (4)
• Per i circuiti nonlineari si può parlare
di stabilità globale e di stabilità locale
• Un circuito è globalmente stabile se la
soluzione non va mai all’infinito,
instabile altrimenti
• La stabilità locale riguarda invece i
punti di equilibrio (circuiti del primo
ordine)
• Il circuito appena visto è globalmente
stabile, mentre due punti di equilibrio
sono stabili e uno instabile
• Nei circuiti lineari la caratteristica è
una retta e esiste solo un punto di
equilibrio, per cui i due concetti di
stabilità locale e globale coincidono
21
Soluzioni particolari
• Esaminiamo ora le soluzioni particolari
per una limitata classe di forzanti,
ovvero per quelle che hanno la derivata
della loro stessa forma funzionale
• Le forzanti in questione sono:
1)
2)
3)
4)
Costante
Sinusoidale
Esponenziale
Polinomiale
22
Condensatore: sorgente costante
• Poniamo: veq(t) = Vs vpC(t) = Vp
Ricordando che
v&C (t ) = −
vC (t )
τC
+
veq (t )
τC
• Si ottiene
0=−
Vp
τC
+
Vs
τC
→ V p = Vs
• La soluzione generale per t ≥ 0 è
vC (t ) = (V0 − V p ) e
−
t
τC
+ V p = V0 e
−
t
τC
t
−
τ
+ V p 1 − e C
• A regime:
vC (t ) ≈ vCp (t ) = V p
→ v&C (t ) = 0 → i (t ) = Cv&C (t ) = 0
• Il condensatore è equivalente a un circuito
aperto
23
Induttore: sorgente costante
• Poniamo: ieq(t) = Is ipL(t) = Ip
Ricordando che
i (t )
&iL (t ) = − iL (t ) + eq
τL
τL
• Si ottiene
0=−
Ip
τL
+
Is
τL
→ I p = Is
• La soluzione generale per t ≥ 0 è
iL (t ) = (I 0 − I p ) e
−
t
τL
+ I p = I0 e
−
t
τL
+
t
−
I p 1 − e τ L
• A regime:
iL (t ) ≈ iLp (t ) = I p
→ i&L (t ) = 0 → v (t ) = Li&L (t ) = 0
• L’induttore è equivalente a un corto circuito
24
Condensatore: sorgente sinusoidale
• Poniamo: veq(t) = Vs cos(ωt + ϕs)
vpC(t) = Vp cos(ωt + ϕp)
• Trattandosi di una soluzione particolare
(o a regime) sinusoidale, possiamo
utilizzare i fasori (valore massimo per
il modulo) per il suo calcolo
p
C
V
=
1
jωC
1
+ Req
jωC
V eq =
1
1 + jω Req C
V eq
dove : V eq = Vs e jϕ s
25
Condensatore: sorgente sinusoidale
(2)
• Per la antitrasformazione, servono il
modulo e la fase di VCp
VC =
p
Vs
1 + ω 2 Req2 C 2
∠VCp = ϕ s − arctg (ω Req C ) + 2kπ
• Infine si ottiene vpC(t)
(
vCp (t ) = VCp cos ωt + ∠VCp
)
• La soluzione generale per t ≥ 0 è
(
(
)
))
vC (t ) = V0 − VCp cos ∠VCp e
(
+ VCp cos ωt + ∠VCp
−
t
τC
+
26
Induttore: sorgente sinusoidale
• Poniamo: ieq(t) = Is cos(ωt + ϕs)
ipL(t) = Ip cos(ωt + ϕp)
• Trattandosi di una soluzione particolare
(o a regime) sinusoidale, possiamo
utilizzare i fasori (valore massimo per
il modulo) per il suo calcolo
1
I
p
L
=
j ωL
1
j ωL
+ Geq
I eq =
1
1 + jω Geq L
I eq
dove : I eq = I s e jϕ s
27
Induttore: sorgente sinusoidale (2)
• Per la antitrasformazione, servono il
modulo e la fase di ILp
I
p
L
=
Is
1 + ω 2Geq2 L2
∠I Lp = ϕ s − arctg (ω Geq L ) + 2kπ
• Infine si ottiene ipL(t)
(
iLp (t ) = I Lp cos ωt + ∠I Lp
)
• La soluzione generale per t ≥ 0 è
(
(
)
))
iL (t ) = I 0 − I Lp cos ∠I Lp e
(
+ I Lp cos ωt + ∠I Lp
−
t
τL
+
28
Sorgente esponenziale
• Poniamo per un condensatore:
veq (t ) = Vs e
−
t
τs
→ vCp (t ) = V p e
−
t
τs
τs ≠ τC
• Per trovare Vp, si può soltanto sostituire
vpC(t) nella equazione differenziale
(deve essere: τC ≠ τs)
−
Vp
τs
−
e
t
τs
=−
Vp
τC
−
e
t
τs
+
Vs
τC
−
e
t
τs
∀t
• Semplificando l’esponenziale (sempre
≠ 0), si ottiene una equazione in Vp
Vs
Vp =
1
1
τ C −
τC τ s
29
Sorgente esponenziale (2)
• La soluzione generale per t ≥ 0 è
vC (t ) = (V0 − V p ) e
−
t
τC
+ Vpe
−
t
τs
• Per gli induttori vale un discorso
analogo per cui
I eq (t ) = I s e
−
t
τs
→ i (t ) = I p e
p
L
−
t
τs
τs ≠ τL
Is
Ip =
1
1
τ L −
τ L τ s
iL (t ) = (I 0 − I p ) e
−
t
τL
+ I pe
−
t
τs
30
Sorgente polinomiale
• Consideriamo una generica sorgente
(per l’esempio di grado 2)
xeq (t ) = a0 + a1t + a2t 2
→ x p (t ) = k0 + k1t + k 2t 2
• Per l’equazione differenziale
x& (t ) = −
x (t )
+
xeq (t )
τ
τ
• Sostituendo la soluzione particolare si
trova
k1 + 2k 2t = −
+
a0
τ
+
a1t
τ
+
k0
τ
−
a2 t 2
τ
k1t
τ
−
k 2t 2
τ
+
∀t
31
Sorgente polinomiale (2)
• Dal momento che abbiamo scritto una
identità, perché sia valida per ogni t
dobbiamo eguagliare i coefficienti dei
singoli monomi, il che equivale a
scrivere un sistema di 3 equazioni in 3
incognite, ovvero i parametri k0, k1 e k2
k0 a0
k1 = − τ + τ
k1 a1
2 k 2 = − +
τ
τ
0 = − k 2 + a2
τ
τ
• La soluzione generale per t ≥ 0 è
x(t ) = ( X 0 − k0 ) e
−
t
τ
+ k0 + k1t + k 2t 2
32
Principio di sovrapposizione delle
soluzioni particolari
• Prendiamo ad esempio un circuito RC
del I ordine con 2 sorgenti indipendenti
• La soluzione particolare vpC(t) è
esprimibile come
vCp (t ) = vCp1 (t ) + vCp 2 (t )
• Dove vp1C(t) è associata a vs1(t) e vp2C(t)
è associata a vs2(t)
33
Principio di sovrapposizione delle
soluzioni particolari (2)
• Si ha che: vs(t) = vs1(t) + vs2(t)
1) accendiamo la prima sorgente vs1(t) e
spegniamo la seconda (vs2(t) = 0). La
soluzione particolare associata vp1C(t)
soddisfa l’equazione differenziale del
circuito
p1
v
vs1 (t )
p1
C (t )
v&C (t ) = −
+
τC
τC
2) accendiamo la seconda sorgente vs2(t) e
spegniamo la prima (vs1(t) = 0). La
soluzione particolare associata vp2C(t)
soddisfa anch’essa l’equazione differenziale
del circuito
v&Cp 2 (t ) = −
vCp 2 (t )
τC
+
vs 2 (t )
τC
34
Principio di sovrapposizione delle
soluzioni particolari (3)
• Sommiamo le equazioni appena scritte. Si
ottiene
v& (t ) + v& (t ) = −
p1
C
+
p2
C
vs1 (t )
τC
+
vCp1 (t )
τC
−
vCp 2 (t )
τC
+
vs 2 (t )
τC
• E applicando la proprietà della linearità della
derivata e la proprietà associativa della
somma
(
)
vCp1 (t ) + vCp 2 (t )
d p1
p2
vC (t ) + vC (t ) = −
+
dt
τC
(
)
(
vs1 (t ) + vs 2 (t ) )
+
τC
• Risulta che la soluzione particolare associata
a entrambe le sorgenti è composta dalla
somma delle soluzioni particolari associate
alle singole sorgenti
35
Circuito risonante reale serie
• È un circuito RLC del II ordine (R, L, C > 0)
• Le variabili di stato sono vC(t) e iL(t), a cui
sono associate le condizioni iniziali vC(0) e
iL(0) (= i(0))
vs (t ) = vR (t ) + vL (t ) + vC (t )
vR (t ) = Ri (t )
i (t ) = Cv&C (t )
vL (t ) = Li&(t )
36
Circuito risonante reale serie (2)
• Ne risulta
vs (t ) = RCv&C (t ) + LCv&&C (t ) + vC (t ) ⇒
R
1
1
v&&C (t ) + L v&C (t ) + LC vC (t ) = LC vs (t )
vC (0) = V0
i (0) I 0
=
v&C (0) =
C
C
• Il polinomio caratteristico associato
alla equazione omogenea è
R
1
=0
p + p+
L
LC
2
2
R
1
R
± −
dove : 1p2 = −
2L
LC
2L
37
Circuito risonante reale serie (3)
• La soluzione generale per t ≥ 0 è:
vC (t ) = k1e p1t + k 2 e p2t + vCp (t )
I0
v&C (0) =
vC (0) = V0 ,
C
• Dove k1 e k1 dipendono dalle
condizioni iniziali
• La soluzione particolare viene calcolata
come nel caso dei circuiti del I ordine
• Il circuito è stabile se ℜ{p1} e ℜ{p2}
sono negative
38
Circuito risonante reale serie (4)
L
• Per R ≥ 2
p1 e p2 sono reali C
soluzione omogenea composta da due
esponenziali reali (k1 e k2 sono reali)
• p1 e p2 sono complessi coniugati se:
2
1
L
R
<0→R<2
= 2 z0
−
C
2 L LC
La resistenza deve dissipare «poca
energia» rispetto a quella
immagazzinata dagli elementi reattivi
(z0: impedenza caratteristica)
39
Circuito risonante reale serie (5)
• Se p1 e p2 sono complessi coniugati,
p1 = σ + jω, p2 = σ – jω,
perché la soluzione vC(t) sia reale k1 = k*2 = | k1 |ejϕ
• Si trova quindi
vC (t ) = 2eσ t ℜ{k1e jω t } + vCp (t ) →
vC (t ) = 2 k1 eσ t cos(ωt + ϕ ) + vCp (t )
v&C (0) = I 0 / C
vC (0) = V0 ,
40
Circuiti di ordine n in t
• Per un circuito non degenere LDI di ordine n
(n = nD: numero di componenti dinamici),
possiamo scrivere o una equazione
differenziale di ordine n oppure un sistema di
n equazioni differenziali del I ordine. Di
norma si utilizza quest’ultimo metodo.
Indicando con xk la generica variabile di stato,
si ottiene la seguente equazione vettoriale di
stato
x& (t ) = Ax(t ) + Bu (t )
x(0) = X 0
• Nel caso di un circuito risonante serie, si ha
1
0
v
(
t
)
v&C (t ) 0
C
C
=
+ 1 vs (t )
i&(t ) 1
R i (t )
−
−
L
L
L
vC (0) = V0 , i (0) = I 0
41
Circuiti di ordine n in t (2)
• Gli autovalori della matrice A sono
p
det( pI − A) =
1
L
1
C = p2 + R p + 1 = 0
R
L
LC
p+
L
R
1 p2 = −
2L
−
2
+
−
1
R
−
2 L LC
• p1 e p2 sono le frequenze naturali del
circuito
• Coincidono con le radici del polinomio
caratteristico
42
Circuiti di ordine n in t (3)
• La soluzione generale è
x(t ) = k1ξ1e
p1t
+ k 2ξ 2 e
p2t
+ x (t )
p
• Dove ξ1 e ξ2 sono gli autovettori di A e
k1 e k2 dipendono dalle condizioni
iniziali
pt
p t
• e 1 e e 2 sono i modi naturali del
circuito
• Se p1 e p2 sono complessi coniugati, lo
saranno pure ξ1 e ξ2 e k1 e k2
• N.B. queste costanti k1 e k2 sono
diverse da quelle utilizzate nella
risoluzione della equazione del II
ordine
43
Circuiti di ordine n in t (4)
• La soluzione generale può essere
scritta in altra forma equivalente alla
precedente
(
)
p
p
A
t
x(t ) = e X 0 − x (0) + x (t )
• L’esponenziale di matrice viene
calcolato sulla base degli autovalori e
autovettori della matrice A
44
Sovrapposizione delle
condizioni iniziali
• Consideriamo un circuito LDI di
ordine n senza sorgenti indipendenti
x& (t ) = Ax(t )
x ( 0) = X 0
• La soluzione è
x(t ) = e At X 0
• Dove
x01
x
02
X0 =
M
x0 n
45
Sovrapposizione delle
condizioni iniziali (2)
• Vale il principio della sovrapposizione
delle condizioni iniziali per cui
x(t ) = e At X 0 =
0
x01
0
0
0
x
= e At + e At 02 + K + e At
M
M
M
0
0
x0 n
46
Stabilità (circuiti lineari)
• Un circuito lineare è stabile se le parti
reali delle frequenze naturali
(autovalori) p1, p2 …, pn sono negative
• Un circuito lineare stabile senza
sorgenti indipendenti, lasciato evolvere
da una certa condizione iniziale,
tenderà a dissipare tutta l’energia
contenuta nei componenti reattivi, per
cui le variabili di stato tenderanno a
zero come il tempo tende all’infinito
47
Stabilità (locale) alla Liapunov
• Una soluzione x(t) [nx1] di un circuito
nonlineare, definita nell’intervallo [t0,∞), è
asintoticamente stabile se, per ogni ε > 0,
esiste un δ > 0 tale che ogni soluzione x1(t)
per cui vale
x1 (t0 ) − x(t0 ) < δ
• soddisfa
lim x1 (t ) − x(t ) < ε
t →∞
• Nei circuiti nonlineari la stabilità locale è
limitata alla singola soluzione, non si può
estendere al circuito
• Nei circuiti lineari si dimostra che la stabilità
di una soluzione si può estendere alla stabilità
di tutte le soluzioni (nonché dei punti di
equilibrio) e quindi alla stabilità del circuito
stesso
48
Altre variabili del circuito
• Ricordiamo le equazioni di uscita della
teoria dei sistemi
x& (t ) = Ax(t ) + Bu (t )
y (t ) = Cx(t ) + Du(t )
x(0) = X
0
• Le variabili del circuito (tensioni,
correnti, potenziali), espresse come
y(t), sono una combinazione lineare
dello stato e degli ingressi.
• Nei circuiti si ricorre al teorema di
sostituzione per ricavare un circuito
resistivo associato al circuito dinamico
originale, la cui soluzione dia le
variabili cercate
49
Teorema di sostituzione
• Se N (circuito completo in alto) ha
un’unica soluzione v = vs(t) (i = is(t) )
per ogni t, allora NL può essere
sostituita da una sorgente di tensione
vs(t) (corrente is(t) ) senza influenzare
le tensioni e le correnti dentro NR,
ammesso che Nv (Ni) abbia un’unica
soluzione per ogni t
50
Circuito resistivo associato
• Applicando il teorema di sostituzione, i
condensatori sono sostituiti con dei generatori
di tensione di valore vC(t) e gli induttori con
dei generatori di corrente di valore iL(t).
• Risolvere questo circuito resistivo equivale a
scrivere le equazioni di uscita
51
Circuiti degeneri
• Prendiamo in considerazione un
circuito in cui le variabili di stato siano
soggette a una o più relazioni lineari,
non siano quindi linearmente
indipendenti tra loro. Esempio
• v1(t) − v2(t) − v3(t) = 0
• In questo circuito: nD = 4, nLin = 1
• In virtù della relazione lineare, l’ordine
del circuito è: n = nD – nLin = 3
• La matrice A ha dimensioni [3x3]
52
Circuiti degeneri (2)
• Risolta l’equazione di stato, le variabili
di uscita vengono calcolate come nel
caso non-degenere con una avvertenza:
• Questo circuito ha infinite soluzioni, in
quanto non è determinata la corrente
nella maglia dei condensatori
• Sostituisco allora uno dei generatori di
tensione con un generatore di corrente
che sostenga la corrente del
condensatore, ovvero ik = Ck v&k
53
Parallelo e serie di C e L
• Un circuito con due condensatori in
serie è molto diverso da un circuito con
due condensatori in parallelo. Lo stesso
dicasi per gli induttori
• Due condensatori in serie (induttori in
parallelo) hanno le tensioni (correnti)
indipendenti, quindi corrispondono a
due variabili di stato
• Due condensatori in parallelo (induttori
in serie) hanno le tensioni (correnti)
dipendenti linearmente, quindi
corrispondono a una variabile di stato
54
Parallelo e serie di C e L (2)
• Parallelo di due condensatori:
Cp = C1 + C2
• Serie di due condensatori:
Cs = (C1 C2)/(C1 + C2)
• Serie di due induttori:
Ls = L1 + L2
• Parallelo di due induttori
Lp = (L1 L2)/(L1 + L2)
55
Partitori di C e L
• Un partitore di tensione realizzato con
due condensatori o due induttori
permette di avere un rapporto di
riduzione indipendente dalla frequenza
• Elemento importante: non dissipano
potenza attiva come le resistenze
• N.B. A causa del fatto che il
condensatore sta al denominatore
dell’impedenza, si ha che
V1
C2
=
Vs
C1 + C2
56
Presenza di un interruttore
• L’interruttore è un componente
resistivo tempo-variante.
• Consideriamo un interruttore ideale, il
cui stato aperto corrisponde a un
circuito aperto e lo stato chiuso a un
corto circuito
• Divideremo lo studio del circuito in
due parti, per t ≤ t0 e t ≥ t0, dove t0 è
l’istante in cui l’interruttore commuta
• Per collegare le due evoluzioni
temporali, utilizzeremo il principio di
continuità delle variabili di stato
57
Principio di continuità delle
variabili di stato
• Consideriamo la tensione su un
condensatore (idem per un induttore)
1
∆t →0 C
vC (t + ∆t ) − vC (t ) = lim
t + ∆t
∫ i(τ )dτ
=0
t
se : i (τ ) < M
58
Transitori con Laplace
• Trasformando l’equazione matriciale di
stato con Laplace
sX( s ) − x(0 − ) = AX( s) + BU ( s )
[sI n − A ]X(s) = x(0 − ) + BU( s)
−1
−1
X( s) = [sI n − A ] x(0 − ) + [sI n − A ] BU ( s )
1442443 144
42444
3
soluzione libera
soluzione forzata
• Il denominatore della X(s) è dato da
det[sIn – A] circuito stabile se tutti i
poli (coincidenti con gli autovalori di
A) sono a parte reale negativa
• Nel dominio del tempo si ottiene
p
x(t ) = e At (X 0 − x p (0) ) +
x{
(t )
1442443
soluzione a
soluzione
regime
transitoria
59