Banda passante di un amplificatore
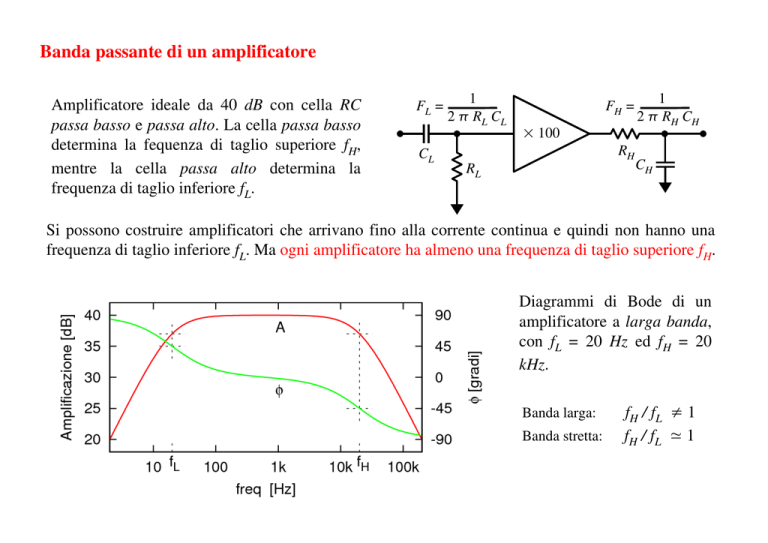
Amplificatore ideale da 40 dB con cella RC passa basso e passa alto. La cella passa basso determina la fequenza di taglio superiore fH, mentre la cella passa alto determina la frequenza di taglio inferiore fL.
FL = 1 2 RL CL
CL
RL
× 100
FH = 1 2 RH CH
RH
CH
Si possono costruire amplificatori che arrivano fino alla corrente continua e quindi non hanno una frequenza di taglio inferiore fL. Ma ogni amplificatore ha almeno una frequenza di taglio superiore fH.
Diagrammi di Bode di un amplificatore a larga banda, con fL = 20 Hz ed fH = 20 kHz.
Banda larga: fH / fL ≠ 1
Banda stretta: fH / fL ≃ 1
Risposta all'onda quadra di un amplificatore a banda larga – fronte di salita
Banda passante: 20 Hz – 20 kHz
Uscita
tr : tempo di salita (rise time)
tr = t90% ­ t10%
= [ log (0.9) – log (0.1) ]
= log (9) = 2.2 ∙
= 2.2 / (2 fH) = 0.35 / fH
Ingresso
tf : tempo di discesa (fall time)
In un amplificatore lineare tempo di salita e tempo di discesa sono identici.
Ingrandimento del fronte di salita
Risposta all'onda quadra di un amplificatore a banda larga – tilt
Al termine del fronte di salita inizia il decadimento esponenziale tipico all'uscita di una cella passa­alto:
v(t) = vi exp (­t / L)
L = RLCL = 1 / (2 fL) = vi / dv/dt
vi : tensione iniziale
dB
Risposte di un circuito passa basso
in
R
out
C
frequenza (kHz)
—— fH = 3 kHz RC = 1/2fH = 53 s —— fH = 10 kHz RC = 1/2fH = 16 s
—— fH = 30 kHz RC = 1/2fH = 5.3 s
tempo (ms)
fig:low_pass
dB
Risposte di un circuito passa alto
in
out
C
R
frequenza (kHz)
—— fH = 300 Hz RC = 1/2fH = 0.53 ms —— fH = 100 Hz RC = 1/2fH = 1.6 ms
—— fH = 30 Hz RC = 1/2fH = 5.3 ms
tempo (ms)
fig:low_pass
dB
Risposte di un circuito passa banda
in
CL
RH
CH
out
RL
frequenza (kHz)
—— fH / f = f / fL = 3
—— fH / f = f / fL = 10
—— fH / f = f / fL = 100
tempo (ms)
fig:low_pass
Risposta di un amplificatore con frequenze di taglio multiple
12.9 kHz
Banda passante di un amplifcatore con due frequenza di taglio fH:
—— fH1 = fH2 = 20 kHz
—— fH1 = 20 kHz fH2 = 200 kHz
19.8 kHz
—— fH = 20 kHz (singola)
20 dB per decade
40 dB per decade
Risposta all'onda quadra di un amplificatore con frequenze di taglio multiple
—— fH1 = fH2 = 20 kHz 1,2 = 7.96 s tr = 27 s
—— fH1 = 20 kHz fH2 = 200 kHz 1,2 = 7.96 , 0.796 s tr = 17.6 s
—— fH = 20 kHz (singola) 1 = 7.96 s tr = 17.5 s
In prima approssimazione, i tempi di salita si sommano quadraticamente. (17.5 ∙ √ 2 = 24.7)
Dipendenza dei parametri del bjt dalla frequenza
Rg
a)
b
c
ĝre vce
VG
ĝie
ĝfe vbe
ĝoe
e
RL
e
Al crescere della frequenza i parametri g diventano funzioni complesse: ĝ()
Capacita' di diffusione della giunzione base­emettitore in polarizzazione diretta
Rg
b)
Capacita' di transizione della giunzione base­collettore contropolarizzata
CT b
gie
VG
e
CD gfe vbe
c
goe
RL
e
Si aggiungono al circuito due capacita' estranee al modello: CT e CD
Capacita' di diffusione CD
Rg
CT b
VG
gie
CD gfe vbe
e
c
goe
RL
e
Capacita' di diffusione della giunzione base­emettitore in polarizzazione diretta
Per un diodo in conduzione: CD rd =
rd = resistenza dinamica del diodo = 1 / gd = VT / IE
Per un transistor: = ( 2 fT )­1 fT = frequenza di transizione ; gd = gfe
CD =
g fe
2 f T
=
IE
2 f T V T
Esempio: transistor CA3046 con IE = 0.74 mA:
fT = 400 MHz gd = 20 mA/V
CD ≃ 9 pF
Capacita' di transizione della giunzione base­collettore contropolarizzata
Capacita' di transizione CT
Rg
CT b
gie
VG
CD gfe vbe
e
c
goe
RL = 10 k e
Capacita' di transizione per un transistor
del chip CA3046
0.45 pF
Effetto Miller
Rg
CT (0.45 pF)
b
gie
VG
e
Ci gfe vbe
c
Co goe
CD
(9 pF) RL
e
Con guadagno di tensione Av = ­140 il condensatore CT tra ingresso ed uscita equivale alla capacita' di Miller Ci = CT ∙ (1 ­ Av) = 63 pF all'ingresso e alla capacita' Co = CT ∙ (1 ­ Av) / Av = 0.45 pF all'uscita.
La costante di tempo di ingresso diventa
i = ( Ci + CD ) / gie = (63 + 9) pF / 0.25 mA/V = 0.29 s
e la frequenza di taglio
fi = 1 / (2 0.29 s) = 0.55 MHz
La resistenza Rg interna del generatore si aggiunge in parallelo a gie e riduce la costante di tempo, aumentando la banda passante (a spese della corrente fornita dal generatore VG).
La costante di tempo all'uscita e': o = Co ∙ (goe // RL ) ≃ 0.45 pF ∙ 10 k = 4.5 ns.
I transistor ad effetto di campo in alta frequenza
C gd
d
g
C gs
g fs v gs
gds
s
Cgs = capacita' gate­source
Cgd = capacita' gate­drain
Csb = capacita' source­substrato
Cdb = capacita' drain­substrato
C db
b
C sb
s
Modello lineare per il transistor mosfet in alta frequenza.
C gd
Ai circuiti in corrente continua vengono aggiunte le capacita' tra source, drain e gate e le capacita' delle giunzioni PN tra source, drain e bulk (nel mosfet).
d
g
C gs
s
ggs
g fs v gs
gds
C ds
Modello lineare per il transistor jfet in alta frequenza.
s
Banda passante di un amplificatore ad emettitore comune
Modulo e fase del guadagno:
—— di tensione
—— di corrente
—— di potenza
Condizioni di lavoro:
RL 10 k
RG 50
IE 0.72 mA
VCE 8.5 V
AI 106
AV 250
gfe 27 mA/V
gie 0.24 mA/V
goe 6.6 A/V
CD 9.1 pF
CT 0.44 pF
Ccs 0.5 pF
Impedenza di ingresso di un amplificatore ad emettitore comune
Modulo e fase dell'impedenza di ingresso di un amplificatore ad emettitore comune
Impedenza di uscita
Zo
vo
vi
Misura della impedenza di uscita
RL
Senza la resistenza di carico RL si misura la tensione
v1 = vo
Con la resistenza di carico RL si misura
v2 = vo RL / (Zo + RL)
Risolvendo:
Zo = (v1 / v2 – 1) RL
Misure in alta frequenza
10 k
Capacita' del cavo: ~ 100 pF/m
Costante di tempo = 10 k 100 pF = 1 s FH = 1 / 2 = 160 kHz
La capacita' del cavo interferisce pesantemente con il funzionamento del circuito in misura
Misure in alta frequenza
La sonda dell'oscilloscopio contiene un partitore compensato che riduce di un fattore 10 l'inetnsita' del segnale e la capacita' collegata al circuito.
13 pF
out
in
9 M
120 pF
1 M
Risposta di un partitore compensato
dB
CH
out
in
RH
CL
RL
frequenza (kHz)
RL/ (RH + RL) = 0.1
—— CH/ (CH + CL) = 0.08
—— CH/ (CH + CL) = 0.10
—— CH/ (CH + CL) = 0.12
tempo (ms)
fig:low_pass
Calibrazione della sonda dell'oscilloscopio
Onda quadra 1 kHz 0.5 V
Regolazione di CL Calibrazione della sonda dell'oscilloscopio