PUNTI NOTEVOLI NEI TRIANGOLI
PUNTI NOTEVOLI NEI TRIANGOLI
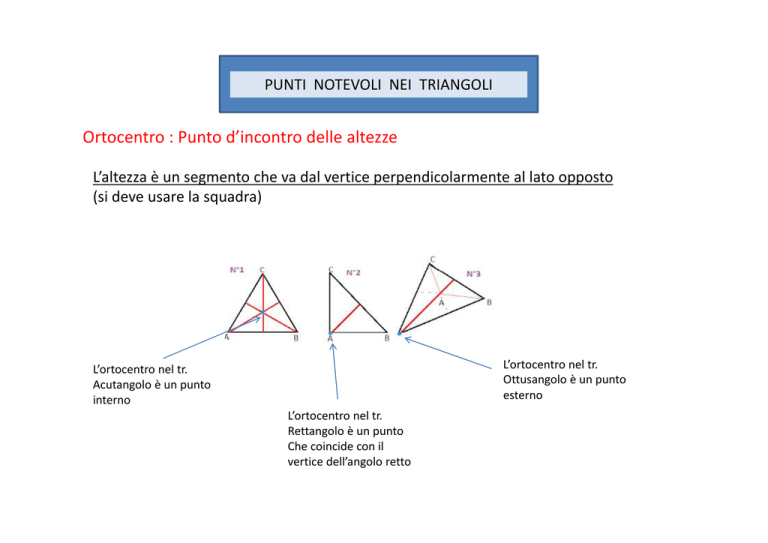
Ortocentro : Punto d’incontro delle altezze
L’altezza è un segmento che va dal vertice perpendicolarmente al lato opposto (si deve usare la squadra)
L’ortocentro nel tr. Ottusangolo è un punto esterno
L’ortocentro nel tr. Acutangolo è un punto interno
L’ortocentro nel tr. Rettangolo è un punto Che coincide con il vertice dell’angolo retto
Baricentro : Punto d’incontro delle mediane
a ce o u o d co o de e ed a e
LLa mediana è un segmento che va dal vertice al punto medio del lato opposto di
è
t h
d l
ti
l
t
di d l l t
t
(si deve usare il righello per prendere il punto medio)
Il baricentro è sempre un punto interno al triangolo.
Il Baricentro divide le mediane in due parti : una il doppio dell’altra
Il Baricentro divide le mediane in due parti : una il doppio dell
altra BG BG =2
2 GM; GM;
AG =2GP CG = 2GN
I
Incentro : Punto d’incontro delle Bisettrici
t
P t d’i
t d ll Bi tt i i
La bisettrice è una semiretta che divide l’angolo in due parti uguali(si deve usare il goniometro oppure compasso e riga)
L’incentro è sempre interno al triangolo, è equidistante dai lati del triangolo quindi è il centro di un cerchio inscritto (fig 2) Ricordo che la distanza si prende con la
è il centro di un cerchio inscritto (fig.2). Ricordo che la distanza si prende con la squadra
Circocentro : Punto d’incontro degli assi
L’asse è una retta perpendicolare al lato nel suo punto medio (si deve usare la p p
p
(
squadra)
Il circocentro nel tr. Ottusangolo è un punto esterno
Il circocentro nel tr. Acutangolo è un punto interno
Il circocentro nel tr. Rettangolo è un punto che coincide con il punto medio dell’ipotenusa
Proprietà dei triangoli
Triangolo Isoscele
Triangolo Equilatero
Nel tr. Isoscele l’altezza relativa alla base è anche asse bisettrice e mediana Gli
anche asse, bisettrice e mediana. Gli angoli alla base sono uguali. L’ortocentro, l’incentro , il baricentro e il circocentro sono allineati sulla retta cui appartiene l’altezza relativa alla base
Il tr. Equilatero ha tutti i lati e tutti gli angoli uguali (60°) ; in esso ortocentro, baricentro, circocentro e incentro coincidono in O
i id
i O
Triangolo Rettangolo
g
g
Nel tr. Rettangolo la mediana relativa all’ipotenusa è uguale a metà
all’ipotenusa è uguale a metà ipotenusa.
Se un triangolo rettangolo è anche Se
un triangolo rettangolo è anche
isoscele avrà gli angoli acuti di 45° e sarà la metà di un quadrato.
Se un triangolo rettangolo ha un angolo di 30
Se
un triangolo rettangolo ha un angolo di 30° e e
l’altro di 60° sarà la metà di un triangolo equilatero quindi avrà il cateto adiacente all’angolo
all
angolo di 60
di 60°uguale
uguale a metà ipotenusa.
a metà ipotenusa.
Criteri di congruenza dei triangoli
g
g
Due poligoni sono congruenti se sovrapposti coincidono perfettamente cioè se hanno ordinatamente tutti i lati corrispondenti uguali e tutti gli angoli
hanno ordinatamente tutti i lati corrispondenti uguali e tutti gli angoli corrispondenti uguali.
Nel caso dei triangoli non serve verificare tutte e sei le uguaglianze ne basta verificare solo tre grazie ai TRE CRITERI DI CONGRUENZA DEI TRIANGOLI
1 Criterio : Due triangoli sono congruenti se hanno due lati corrispondenti e 1°
Criterio : Due triangoli sono congruenti se hanno due lati corrispondenti e
l’angolo compreso congruenti
2° Criterio : Due Triangoli sono congruenti se hanno un lato e gli angoli ad esso g
g
g
g
adiacenti rispettivamente uguali
3° Criterio : Due Triangoli sono congruenti se hanno i lati rispettivamente uguali












