Matematica Finanziaria ed Attuariale

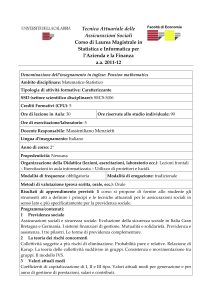
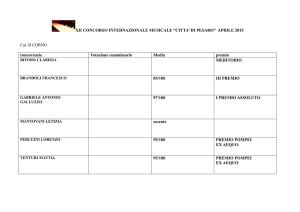
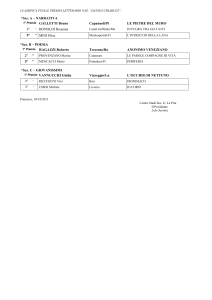
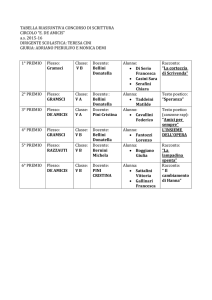
Matematica Attuariale
Prova scritta del 15 febbraio 2005
Si calcoli il premio annuo costante da versare anticipatamente per 20 anni per ottenere una rendita
vitalizia anticipata, differita di 20 anni, con rata annua di € 15 000, per una testa di età x = 40.
Calcolare le riserve matematiche V19,V20, V21, mostrando la coerenza con le relazioni di ricorrenza
di Fouret.
Calcolare l’utile atteso nel 20° e 21° anno del contratto mediante la formula di Homans,
evidenziandone le due componenti finanziarie e demografica.
Allegate le basi tecniche di 1° e 2° ordine.
Durata 1h
Nome
Cognome
Matematica Attuariale
Prova scritta del 15 febbraio 2005
Tracciato per le risposte
Il premio unico puro U del contratto in esame si esprime in forma simbolica ed in funzione delle
basi tecniche del 1° ordine nel modo seguente:
U=
Facendo riferimento alle funzioni di commutazione, il premio unico puro si esprime:
U=
Con i dati del problema, si ottiene U =
Il premio periodico P del contratto in esame si esprime in forma simbolica ed in funzione delle basi
tecniche del 1° ordine nel modo seguente:
P=
Facendo riferimento alle funzioni di commutazione, il premio periodico P si esprime:
P=
Con i dati del problema, si ottiene P =
Le riserve matematiche V19 , V20 , V21 si esprimono in forma prospettiva nel modo seguente
V19 =
V20 =
V21 =
Facendo riferimento alle funzioni di commutazione si esprimono:
V19 =
V20 =
V21 =
E valgono
V19 =
V20 =
V21 =
La relazione di ricorrenza di Fouret si esprime nella forma generale nel modo seguente:
Con riferimento alle riserve in esame essa diventa:
Relazione fra V19 e V20 :
Relazione fra V20 e V21 :
La formula di Homans dice:
Con riferimento agli anni di contratto richiesti essa dà i seguenti valori:
E[u’20] =
E[u’21] =
Le componenti finanziarie e demografiche dell’utile atteso nei due anni sono:
Matematica Attuariale
Prova scritta del 15 febbraio 2005
Traccia di soluzione.
Il premio unico puro U del contratto si calcola nel modo seguente:
  x 1
  x 1
h 0
h 0
U R m / a x  R
 h Ex  R
 1  i 
mh
l xh
N
N
95 046.04
 R x  m  15 000 60  15 000
 71880.7086
lx
Dx
D40
19 834.12
Il premio periodico P del contratto in esame si calcola nel modo seguente:
N xm
Dx
N 60
95 046.04
U
P
R
 15 000
 15 000
 5 271.737937
N x  N xm
a x:m
N 40  N 60
345 486.38  95 046.04
Dx
Le riserve matematiche V19 , V20 , V21 si calcolano in forma prospettiva nel modo seguente
V19  Pr est 19,    Pr emi19,    R
N 60
95 046.04
 P  15 000
 5 271.737937  167 010.7022
D59
8 275.31
V20  Pr est 20,    R
N 60
95 046.04
 P  15 000
 182132.8734
D60
7 827.75
V21  Pr est 21,    R
N 61
87 218.30
 15 000
 176 925.1107
D61
7 394.51
La relazione di ricorrenza di Fouret si esprime nella forma generale nel modo seguente:
Vt  Pt N1  Pt 1 1 E x tVt 1
Per le verifiche successive giova ricordare che:
P20N  0, P20  5271.7347937
P21N  15000, P21  0
Con riferimento alle riserve in esame la relazione di Fouret diventa:
V19   P20  1 E 59V 20  5 271.7347937  1.04 1
V 20  P21N  1 E 60V 21  15 000  1.04 1
82 345
182 132.8734  5 271.7347937  172 282.3683  167 010.6303
83 705
80899
176 925.1107  15000  167 132.941225  182 132.941225
82 345
Si osservi che primo e secondo membro delle relazioni differiscono nelle parti decimali:
V19 : 167010.7022  167010.6303
V20 : 182132.8734  182132.941225
La formula di Homans dice:
 

E u t' 1  Vt  Pt 1 i 'i   Ct 1  Vt 1  q x t  q x' t

Si deve tener conto che, trattandosi di un contratto legato alla durata in vita, si ha:
-
Ct+1 = 0 ed il capitale sotto rischio risulta negativo, pari alla riserva Vt+1 cambiata di segno;
quando è in corso l’erogazione della rendita, ad iniziare dal 21-esimo anno, occorre sottrarre
alla riserva matematica l’importo della rata versata ad inizio periodo;
Con riferimento agli anni di contratto richiesti la formula di Homans dà i seguenti valori:
 


'
'
E u 20
 V19  P20 3%  4%    V20  q59  q59

 83705  82345 87136  86085 
 167010.022  5271.737937 (1%)   182132.8734


83705
87136



.046792
762
396
1724


 

.
  -2486.44
perdita finanziaria
   V
Eu
'
21
19
perdita demografica


'
 R 3%  4%    V21  q 60  q60

 82345  80899 86085  84931 
 182132.8734  15000(1%)  

 176925.1107  
82345
86085



.328734
735
108
1671


 

.
  -2406.44
perdita finanziaria
perdita demografica