06_BJT

•
•
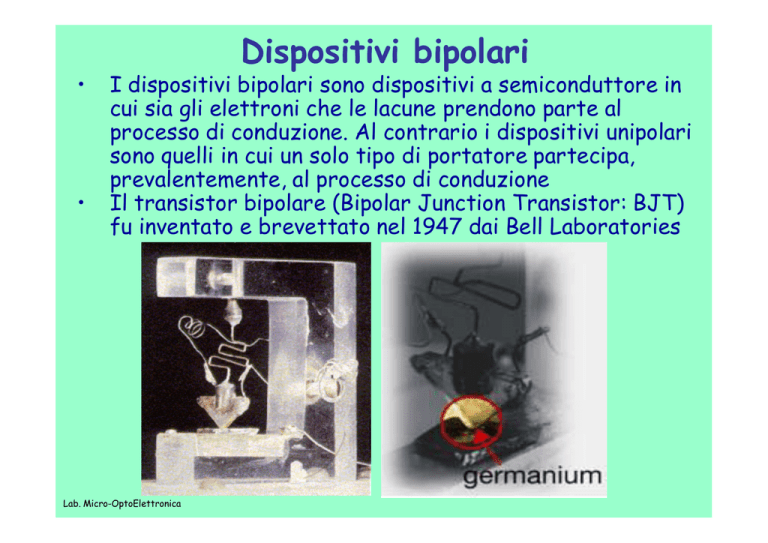
Dispositivi bipolari
I dispositivi bipolari sono dispositivi a semiconduttore in
cui sia gli elettroni che le lacune prendono parte al
processo di conduzione. Al contrario i dispositivi unipolari
sono quelli in cui un solo tipo di portatore partecipa,
prevalentemente, al processo di conduzione
Il transistor bipolare (Bipolar Junction Transistor: BJT)
fu inventato e brevettato nel 1947 dai Bell Laboratories
Lab. Micro-OptoElettronica
•
•
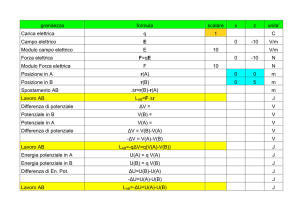
Transistor bipolare a giunzione: BJT
Il transistor bipolare è costituito da due giunzioni p-n
accoppiate (back to back). In figura è mostrata in
sezione una tipica struttura p+-n-p.
La regione più drogata (p+) è detta emettitore, la
regione centrale (n) base e la terza (p) collettore
Lab. Micro-OptoElettronica
Struttura e Modello di
un transistor bipolare n-p-n
•
•
Struttura reale, semplificata, di un moderno transistor
BJT di tipo n-p-n, realizzato in tecnologia planare
Simbolo circuitale del transistor BJT
Lab. Micro-OptoElettronica
Struttura e Modello di
un transistor bipolare p-n-p
•
•
Struttura reale, semplificata, di un moderno transistor
BJT di tipo p-n-p, realizzato in tecnologia planare
Simbolo circuitale del transistor BJT
Lab. Micro-OptoElettronica
Modi di funzionamento
VBE
Attivo
Saturazione
VBC
Interdizione
Invertito
• in alto diagramma a bande
• in basso densità elettronica
Lab. Micro-OptoElettronica
Modi di funzionamento
a) Polarizzazione nulla: equilibrio termico
b) Entrambe le giunzioni pol. inversamente (interdizione OFF )
c) Entrambe le giunzioni pol. direttamente (saturazione ON )
d) Prima giunzione pol. direttamente , seconda giunzione pol.
inversamente (modo attivo)
Lab. Micro-OptoElettronica
Modo attivo (p+-n-p)
Lab. Micro-OptoElettronica
Modo attivo (p+-n-p)
•
•
•
•
Lacune entrano da E→B in gran numero (pol. diretta E-B)
Pochi elettroni da B→E (effetto diverso livello drogaggio)
Corrente di emettitore → base
Lacune iniettate da E nella corta regione di base, possono
diffondere fino al collettore
• Raggiunta la zona di svuotamento sono estratte dal campo
elettrico (pol. inversa B-C): corrente di collettore
Lab. Micro-OptoElettronica
Modo attivo (p+-n-p): correnti
Lab. Micro-OptoElettronica
Modo attivo (p+-n-p)
• Efficienza di emettitore γ: rapporto tra
I Ep
I Ep
γ=
=
la corrente di lacune iniettate e la
I E I En + I Ep
corrente totale di emettitore
• Fattore di trasporto αT in base: rapporto tra la
I Cp
corrente di lacune che diffondono nel collettore
αT =
e quella delle lacune iniettate nella base
I Ep
dall’emettitore
• αT tende ad uno al diminuire della lunghezza di base
• Complessivamente si definisce guadagno del transistor
I Cp
I Cp
I Ep
I C I Cp + I Cn
1
α=
=
≅
=
= αT
= αT γ
I E I En + I Ep I En + I Ep I Ep 1 + ( I En I Ep )
I En + I Ep
IC
IC
IC I E
α
β=
=
=
=
I B I E − IC 1 − IC I E 1 − α
Lab. Micro-OptoElettronica
se α → 1
β →∞
Modo attivo (p+-n-p): teoria BJT ideale
• Componenti della corrente totale di emettitore
Lab. Micro-OptoElettronica
Modo attivo (p+-n-p): teoria BJT ideale
• Componenti della corrente totale di emettitore
• Componenti della corrente totale di collettore
Lab. Micro-OptoElettronica
Modo attivo (p+-n-p): teoria BJT ideale
• Per risolvere le eq. precedenti è necessario conoscere la
distribuzione dei minoritari, utilizzando l’eq. di continuità
con le ipotesi (nella regione di base):
• Bassi livelli di iniezione
• Campo elettrico per minoritari trascurabile
• Nessuna componente di generazione
• Stato stazionario
• Senza ricombinazione dei minoritari (τ=∞) la soluzione è
δ pn ( x′ ) = A1 x + A2
Lab. Micro-OptoElettronica
Modo attivo (p+-n-p): teoria BJT ideale
• Calcoliamo A1, A2 dalle condizioni al contorno per x=0 e x=W
quindi
• Si ricava quindi una dipendenza lineare che è determinata
dall’assenza di fenomeni di ricombinazione: tutte le lacune
iniettate raggiungono la giunzione B-C.
Lab. Micro-OptoElettronica
Modo attivo (p+-n-p): teoria BJT ideale
• Analogamente per la diffusione degli elettroni
In questo caso non si può
trascurare la ricombinazione,
quindi la soluzione sarà del tipo
• In definitiva si ricava
Lab. Micro-OptoElettronica
Modo attivo (p+-n-p): teoria BJT ideale
• Riportando in grafico i risultati ottenuti
Lab. Micro-OptoElettronica
Modo attivo (p+-n-p): teoria BJT ideale
• Per ricavare IE dobbiamo determinare IEp e IEn:
• E’ stata ignorata la ricombinazione di elettroni nella regione
di base e l’iniezione di buche dal collettore. Si è invece
tenuto conto della ricombinazione di lacune in base, anche
se non nelle regioni di svuotamento.
Lab. Micro-OptoElettronica
Modo attivo (p+-n-p): teoria BJT ideale
• La corrente IC di collettore si ricava in modo analogo (buche
provenienti dalla base + elettroni provenienti dal collettore)
analogamente
• Nel modo attivo (VCB<0), quindi IC diventa
• IC ~ IE a parte piccoli termini (ricombinazione +iniez. minor.)
Lab. Micro-OptoElettronica
Modo attivo (p+-n-p): teoria BJT ideale
• La corrente IB si ricava dalla legge di Kirchoff(considerando
il transistor come un nodo)
ma IC ~ IE quindi
nel dettaglio
• L’unico termine di cui teniamo conto è IB2 , che si ricava
dalla carica necessaria per la corrente di ricombinazione
(carica totale diviso il tempo di vita dei portatori):
Lab. Micro-OptoElettronica
Modo attivo (p+-n-p): teoria BJT ideale
• Dalle eq. precedenti
Iniezione elettroni B→E
Iniezione elettroni C→B
Da cui:
Questa espressione tiene
conto della ricombinazione
in base, della corrente di
saturazione inversa di C-B
e della corrente di
elettroni iniettati in E
• Se si tiene conto solo della
ricombinazione IB2
Lab. Micro-OptoElettronica
Caratteristiche di uscita: base comune
• BJT p-n-p
• IC=cost≈IE
quindi α=1
• IC=0 con una piccola pol. diretta ~1 V (in Si) alla giunzione B-C
e si entra nel modo di saturazione
Lab. Micro-OptoElettronica
Evoluzione strutture BJT
Lab. Micro-OptoElettronica
Evoluzione strutture BJT
anni 90
Lab. Micro-OptoElettronica
Base con drogaggio graduato
• Distribuzione
impurezze in base
non uniforme
• Diffusione elettroni
verso collettore
• Campo elettrico
nella regione neutra
di base
• Il campo “aiuta” il
moto delle lacune
iniettate da E in C
• Riduzione tempo di
transito in base e
del fattore di
trasporto αT
Lab. Micro-OptoElettronica
Non-idealità: Resistenza di base
• Nel punto A
VEA=VEB-½IB(RAD+RDB)
• Nel punto D
VED=VEB-½IBRDB
• Quindi se RAD è grande
allora VED > VEA
• Al bordo dell’emettitore
in D l’iniezione di lacune
sarà più intensa
• La maggior parte della
corrente di emettitore si
addenserà sui bordi e
molto meno nella zona centrale “edge crowding”
• Si verificano effetti indesiderati di alti livelli di iniezione
• Soluzione: aumentare il perimetro dell’emettitore
Lab. Micro-OptoElettronica
Non-idealità: Resistenza di base
Strutture interdigitate
Lab. Micro-OptoElettronica
Configurazione a emettitore comune
• Più spesso si adotta la configurazione a emettitore comune
nella config. ad emettitore comune
da cui
I C (1 − α 0 ) = α 0 I B + I CB 0
Lab. Micro-OptoElettronica
I C = α 0 I E + I CB 0 = α 0 ( I B + I C ) + I CB 0
α0
I CB 0
ossia I C =
IB +
1 − α0
1 − α0
Configurazione a emettitore comune
• Indichiamo con β0 l’amplificazione di corrente a emettitore
comune
• β0 = (variazione di IC)/(variazione di IB)
∆I C
α0
β0 =
=
∆I B 1 − α 0
ponendo I CE 0
I CB 0
=
1 − α0
• Che corrisponde alla corrente di dispersione tra collettore ed
emettitore per IB=0
I C = β 0 I B + I CE 0
• poiché α0 è prossimo ad 1, β0 è un numero molto grande:
• una piccola corrente di base può produrre una corrente di
collettore molto più intensa
Lab. Micro-OptoElettronica
Amplificazione con un BJT - 1
(Colinge)
Lab. Micro-OptoElettronica
Amplificazione con un BJT - 2
IC
Lab. Micro-OptoElettronica
IB
Amplificazione con un BJT - 3
esempio
Lab. Micro-OptoElettronica
Modulazione larghezza di base: Effetto Early
• Fissata IB, la corrente di collettore IC dovrebbe rimanere
costante in funzione di VEC, per VEC > 0
• La deviazione dal comportamento ideale è dovuto alla
riduzione dell’ampiezza della regione neutra di base, che
determina un incremento il gradiente di concentrazione e
quindi di IC.
Lab. Micro-OptoElettronica
Tensione di rottura
a base aperta IE=IC=I,
quindi
M=
1
1 − (V BVCB 0 )
η
β0 =
M (α 0 I + I CB 0 ) = I
∆I C
α0
=
∆I B 1 − α 0
ponendo I CE 0 =
MI CB 0
da cui I =
1 − α0M
I CB 0
1 − α0
per α 0 M = 1 la corrente
è limitata solo dal circuito
esterno, quindi
BVCE 0 = BVCB 0 (1 − α 0 )
1η
per Si
; BVCB 0 ( β 0 )
−1 η
2 < η < 6 e β 0 è piuttosto grande quindi BVCE 0 < BVCB 0
Lab. Micro-OptoElettronica
Generazione-ricombinazione
Alti livelli di iniezione
Lab. Micro-OptoElettronica
Modello di Ebers-Moll
qVCB
qVEB




kT
kT
IE = IF0  e
− 1 − α R I R 0  e
− 1




qVCB
qVEB




kT
kT
IC = α F I F 0  e
− 1 − I R 0  e
− 1




α
Lab. Micro-OptoElettronica
α
Frequenza di taglio
• Il più importante limite alla risposta in frequenza di un BJT è
il tempo di transito dei minoritari in base
distanza percorsa dal portatore dx = v ( x ) dt
la corrente risultante I p = q v ( x ) p ( x )
tempo di transito τ B = ∫
W
0
W q p ( x) A
dx
=∫
dx
v ( x) 0
Ip
2
W
per una distribuzione lineare τ B =
2Dp
OTTIMIZZAZIONE τB
• Rendere la base più sottile possibile
• Elevata costante di diffusione (transistor n-p-n)
Lab. Micro-OptoElettronica
Commutazione (BJT in elettronica digitale)
Lab. Micro-OptoElettronica
Tempo di Commutazione
 I Bτ p 
tS ≡ t3 − t2 ; τ p ln 

 QS 
τ p = tempo di vita
minoritari in base
QS = carica
immagazzinata in
base
Lab. Micro-OptoElettronica