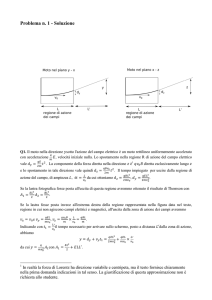
Moto di cariche in campo elettrico uniforme
Problema 1
Un elettrone viene sparato perpendicolarmente, dall’estrerno e verso la lastra carica negativamente, in un
orifizio di una doppia lastra con velocità v0 = 4·105 m/s. Sapendo che il modulo campo elettrico all’interno
della doppia lastra è E = 3·102 V/m e che la velocità di uscita dalla lastra carica positivamente è v = 106 m/s,
calcola la distanza δ tra le due lastre.
Risoluzione:
La situazione reale è rappresentata in figura. Ricordiamo che
l’elettrone ha carica e= -1,6·10-12C e massa me =9,1·10-31Kg, e
che entrando nella doppia lastra come in figura subisce l’azione
del campo elettrico nel verso che va dalla lastra negativa alla
lastra positiva. Inoltre essendo il campo elettrico uniforme
all’interno della lastra, sull’elettrone agirà una forza costante
diretta nello stesso verso di v0, non dimentichiamo che la circa
dell’elettrone è negativa, tale imprimerà all’elettrone
un’accelerazione costante. Dopo queste considerazioni si può dire
che il moto all’interno della doppia lastra sarà Uniformemente
Accelerato, quindi facendo ricorso alla formula che lega la
velocità alla spazio, nel tipo di moto descritto, si ha:
2
2
L’accelarazione sarà: me a=F=Ee Æ
ricordando che v =106 m/s=10·105 m/s , che v0= 4·105 m/s e che E = 3·102 V/m
·
·
·
·
· , ·
, ·
,
79 · 10
·
8 · 10
8
Problema 2
Un protone viene sparato perpendicolarmente, dall’estrerno e verso la lastra carica negativamente, in un
orifizio di una doppia lastra con velocità v0 = 4·105 m/s. Sapendo che il modulo campo elettrico all’interno
della doppia lastra è E = 3·102 V/m e la distanza tra le due lastre è δ=8mm a quale che la velocità il protone
uscirà dalla lastra carica positivamente?
Risoluzione:
La situazione è simile al problema precedente, con la sola differenza che la
forza esercitata dal campo elettrico sul protone è opposta alla velocità,
dunque si avrà un moto uniformente ritardato. Ricordiamo che il protone
ha carica q= -e = 1,6·10-12C e massa mp =1,67·10-27Kg. La formula che
utilizzaremo dopo queste conisderazioni sarà:
2
2
L’accelarazione sarà: mp a=F= Eq Æ
2
2
16 · 10
16 · 10
46 · 10
⁄
2
3 · 10 · 1,6 · 10
1,67 · 10
1600 · 10
39,94 · 10
4,6 · 10
· 8 · 10
/
⁄
⁄
In pratica la stessa velocità! Perché tutta questa differenza elettrone e protone? La risposta, esauriente, è
lasciata come esercizio.
Problema 3
Un elettrone viene sparato con velocità v0=5·105 m/s parallelamente ad una doppia lastra al cui interno il
campo elettrico vale E = 3·10 / . Sapendo che la doppia lastra è lunga 1 cm, si calcoli la distanza h
raggiunta dall’elettrone dopo esser passato all’interno della doppia, considerando un sistema di riferimento
solidale con la posizione iniziale dell’elettrone. Inoltre si determini l’angolo α formato dalla direzione della
velocità di uscita v dell’elettrone rispetto alla direzione iniaziale della velovità v0, e quindi si calcoli il
modulo di v sfruttando quando ottenuto.
Risoluzione:
La situazione è stata ampiamente trattata a lezione, per quanto
riguarda la prima parte, quindi si ha che la traiettoria
dell’elettrone è data dalla parabola
1
2
0, e ciò significa
Nel caso del nostro esercizio
che la parabola descritta rivolge la concavità verso l’alto.
1 3 · 10 · 1,6 · 10
· 25 · 10
2 9,1 · 10
0,01055 · 10
1,05 · 10
(Per esercizio si ricavi m-1 per questo coefficiente)
Quindi l’altezza h = y = Ax2
1,05 · 10
· 10
1,05 · 10
1,05
Ricordiamo,a questo punto, che il vettore velocità è sempre tangente alla traiettoria e che il coefficiente
angola della tangente ad una parabola in un suo punto è dato da:
2
2
Inoltre il coefficiente angolare di una retta è uguale alla tangente goniometrica dell’angolo
retta con il semiasse positivo delle x, ed è proprio l’angolo che cerchiamo.
formato dalla
2
2 · 1,05 · 10 ·
2
· 10
2,1
1,12
64,53°
Infine ricordiamo la scomposizione di vettore rispetto a due direzioni, in questo caso ortogonali
·
·
Quindi
·
,
°
1,162 · 10
⁄
/
11,62 · 10
⁄