Trigonometria
1 di 3
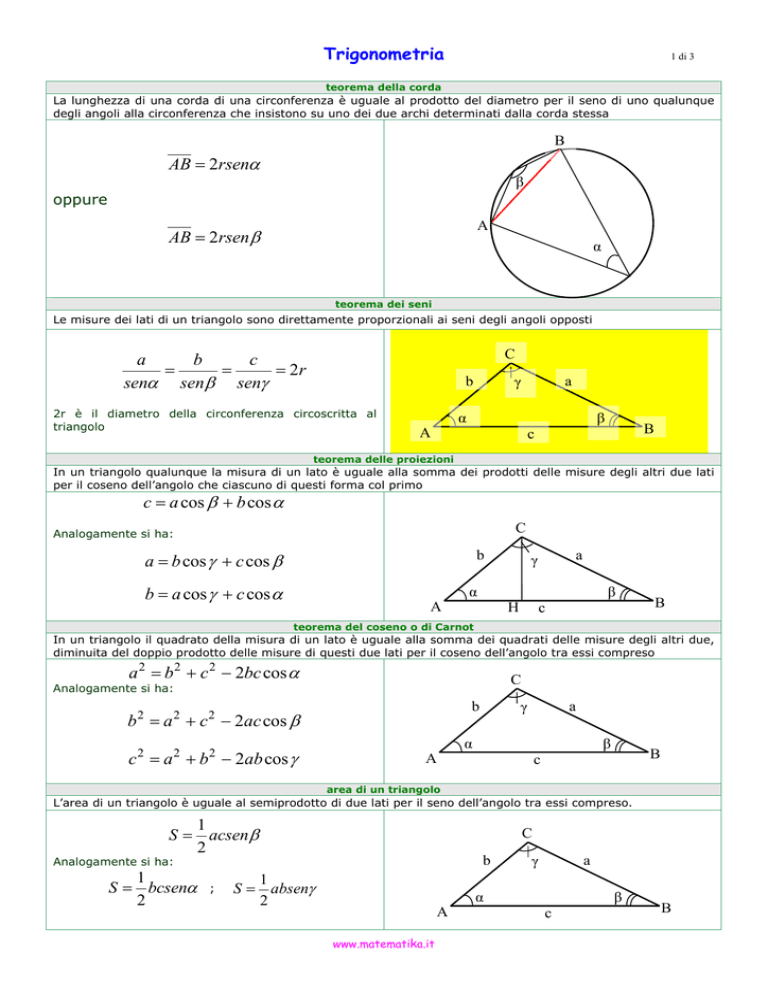
teorema della corda
La lunghezza di una corda di una circonferenza è uguale al prodotto del diametro per il seno di uno qualunque
degli angoli alla circonferenza che insistono su uno dei due archi determinati dalla corda stessa
B
AB = 2rsenα
β
oppure
A
AB = 2rsenβ
α
teorema dei seni
Le misure dei lati di un triangolo sono direttamente proporzionali ai seni degli angoli opposti
C
a
b
c
=
=
= 2r
senα senβ senγ
b
2r è il diametro della circonferenza circoscritta al
triangolo
a
γ
α
A
β
B
c
teorema delle proiezioni
In un triangolo qualunque la misura di un lato è uguale alla somma dei prodotti delle misure degli altri due lati
per il coseno dell’angolo che ciascuno di questi forma col primo
c = a cos β + b cos α
C
Analogamente si ha:
b
a = b cos γ + c cos β
b = a cos γ + c cos α
A
α
a
γ
β
H
c
B
teorema del coseno o di Carnot
In un triangolo il quadrato della misura di un lato è uguale alla somma dei quadrati delle misure degli altri due,
diminuita del doppio prodotto delle misure di questi due lati per il coseno dell’angolo tra essi compreso
a 2 = b 2 + c 2 − 2bc cos α
C
Analogamente si ha:
b
b 2 = a 2 + c 2 − 2ac cos β
c 2 = a 2 + b 2 − 2ab cos γ
A
a
γ
α
β
B
c
area di un triangolo
L’area di un triangolo è uguale al semiprodotto di due lati per il seno dell’angolo tra essi compreso.
1
S = acsenβ
2
C
b
Analogamente si ha:
1
S = bcsenα
2
;
1
S = absenγ
2
A
www.matematika.it
a
γ
α
β
c
B
Trigonometria
2 di 3
formule di Briggs
Le formule di Briggs permettono di determinare le ampiezze degli angoli di un triangolo, note le misure dei lati.
(p = semiperimetro)
sen
α
2
cos
tg
ctg
α
2
α
2
( p − b)( p − c)
bc
=
α
2
sen
p( p − a)
bc
=
β
2
cos
=
( p − b)( p − c)
p( p − a)
=
p( p − a)
( p − b)( p − c)
tg
ctg
β
2
β
2
( p − a )( p − c)
ac
=
β
2
=
sen
p ( p − b)
ac
=
( p − a)( p − c)
p ( p − b)
=
p ( p − b)
( p − a )( p − c)
γ
2
cos
tg
ctg
γ
2
γ
2
( p − a )( p − b)
ab
=
γ
2
=
p( p − c)
ab
=
( p − a )( p − b)
p ( p − c)
=
p( p − c)
( p − a)( p − b)
formula di Erone
La formula di Erone consente di determinare l’area di un triangolo di cui si conoscono le misure dei lati.
(p = semiperimetro)
S=
p( p − a)( p − b)( p − c)
raggio della circonferenza inscritta
Il raggio r della circonferenza inscritta in un triangolo è uguale al rapporto tra l’area del triangolo e il suo
semiperimetro p.
r=
S
p
C
b
Oppure:
r = ( p − a)tg
α
2
= ( p − b)tg
β
2
= ( p − c)tg
γ
γ
a
r
r
r
α
A
β
B
c
2
raggio della circonferenza circoscritta
Il raggio R della circonferenza circoscritta a un triangolo è uguale al rapporto del prodotto dei lati e il quadruplo
dell’area del triangolo.
B
R=
abc
4S
Oppure:
R=
β
c
A
α
a
R
O
b
a
b
c
=
=
2 senα 2 senβ 2 senγ
γ
C
www.matematika.it
Trigonometria
3 di 3
raggio della circonferenza exinscritta
Una circonferenza si dice exinscritta a un triangolo quando è tangente a un suo lato e ai prolungamenti degli
altri due.
Il raggio della circonferenza exinscritta è uguale al rapporto tra l’area del triangolo e la differenza tra il
semiperimetro e la lunghezza del lato a cui è tangente.
A
S
r1 =
p−a
c
b
Analogamente si ha:
a
B
F
E
S
r2 =
p−b
r3 =
C
D
S
p−c
mediane
ma =
1
2b 2 + 2c 2 − a 2
2
A
Analogamente si ha:
mc
α
c
1
2 a 2 + 2c 2 − b 2
mb =
2
B
ma
γ
β
bα =
b+c
α
C
a M
1
2a 2 + 2b 2 − c 2
2
2bc cos
b
bisettrici
2
A
Analogamente si ha:
2ac cos
bβ
bγ =
a+c
c
β
2
2ab cos
a+b
B
γ
2
www.matematika.it
β
α
α
2
2
ba
D a
b
γ
C












