parallelo di due trasformatori

Il trasformatore
PARALLELO DI DUE TRASFORMATORI
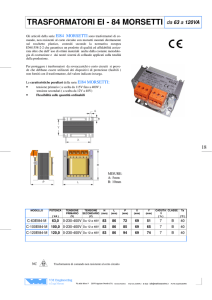
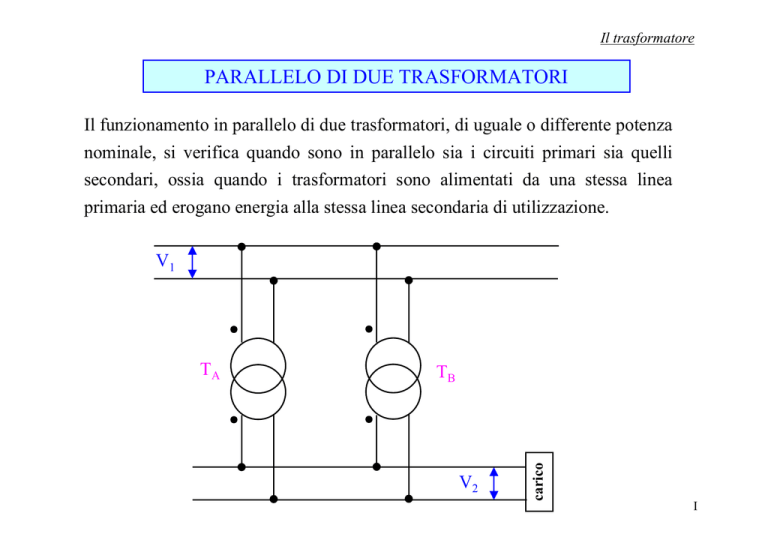
Il funzionamento in parallelo di due trasformatori, di uguale o differente potenza
nominale, si verifica quando sono in parallelo sia i circuiti primari sia quelli
secondari, ossia quando i trasformatori sono alimentati da una stessa linea
primaria ed erogano energia alla stessa linea secondaria di utilizzazione.
V1
TB
V2
carico
TA
I
Il trasformatore
PARALLELO DI DUE TRASFORMATORI
RETE EQUIVALENTE SEMPLIFICATA (riferita a secondario)
V1
e1A
e1B
+
-
+
-
+
-
+
-
e2A
I2A
Z2ccB
I2B
I2
V2
carico
Z2ccA
e2B
II
Il trasformatore
PARALLELO DI DUE TRASFORMATORI
Lo scopo del parallelo di due trasformatori è di distribuire il carico totale in
proporzione diretta alle potenze nominali dei singoli trasformatori.
Una corretta connessione in parallelo richiede che:
• non si abbia circolazione di corrente nei secondari nel funzionamento a vuoto;
• la corrente erogata dal carico si ripartisca tra i trasformatori in modo
proporzionale alle rispettive potenze nominali, con correnti nei trasformatori in
fase tra loro.
Tali condizioni sono soddisfatte se i trasformatori hanno:
a) stesso rapporto di trasformazione;
b) concordanza di fase delle tensioni secondarie a vuoto (stessa polarità);
c) stessa tensione di corto circuito
d) stesso fattore di potenza di corto circuito.
III
Il trasformatore
PARALLELO DI DUE TRASFORMATORI
La condizione a) (stesso rapporto di trasformazione) porta ad avere tensioni
indotte di valore uguale in ogni secondario (e2A = e2B).
Se sussiste anche la condizione b) (concordanza di fase delle tensioni secondarie
a vuoto) nella maglia costituita dai due secondari si ha una tensione indotta
risultante nulla (e2A - e2B = 0).
è nulla la corrente di circolazione nella maglia costituita dai due
secondari, e quindi è nulla la corrente nell’avvolgimento secondario di ciascun
trasformatore.
Le condizioni c) e d) (stessa tensione di corto circuito e stesso fattore di potenza
di corto circuito) permettono la ripartizione del carico totale in proporzione
diretta alle potenze nominali dei singoli trasformatori.
IV
Il trasformatore
PARALLELO DI DUE TRASFORMATORI
Il parallelo di due trasformatori consente di:
1) impiegare più trasformatori di potenza inferiore rispetto a quella
corrispondente al carico totale, nel caso in cui non convenga installare un solo
trasformatore.
2) potenziare l’impianto di trasformazione preesistente, aggiungendo un nuovo
trasformatore.
3) realizzare una trasformazione a rendimento elevato, perché è possibile ridurre
il numero di trasformatori in funzionamento quando il carico si riduce di potenza
e viceversa. Quando il carico si riduce notevolmente, si manterrà in funzione un
solo trasformatore (quello con minori perdite).
4) considerare uno dei due trasformatori in parallelo come riserva, per realizzare
la continuità di esercizio nel caso di guasto di un trasformatore.
V
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE
TRASFORMATORI
Due trasformatori monofase, funzionanti a 50 Hz, sono collegati in parallelo per
alimentare un carico induttivo, con fattore di potenza cosϕcarico = 0,8, da una
sorgente a 11000 V.
Si determini la potenza massima che i trasformatori possono fornire senza che la
tensione sul carico scenda al di sotto di 2250 V.
Si calcoli la potenza fornita dai due trasformatori in questa condizione.
Dati:
Trasformatore A
Trasformatore B
e1n = 11000 V
e1n = 11000 V
e2n = 2300 V
e2n = 2300 V
SnB = 500 kVA
SnA = 100 kVA
VccB = 345 V
VccA = 275 V
Dati provenienti
InBmis = 45,5 A
InAmis = 9,2 A
dalla prova di
corto circuito
PccB = 3370 W
PccA = 1000 W
1
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
Per utilizzare correttamente i dati a disposizione, per prima cosa dobbiamo
capire se la prova di corto circuito è stata effettuata cortocircuitando il primario
oppure il secondario dei due trasformatori.
Per capirlo, calcoliamo le correnti nominali riferite a entrambi i lati dei
trasformatori e confrontiamole con le correnti misurate.
A
B
I1 n A
1 0 0 0 0 0 [V A ]
S nA
=
=
e1n
1 1 0 0 0 [V ]
9, 0 9 [ A ]
I 2 nA
1 0 0 0 0 0 [V A ]
S nA
=
=
e2n
2 3 0 0 [V ]
4 3, 4 8 [ A ]
I1 n B
5 0 0 0 0 0 [V A ]
S nB
=
=
e1n
1 1 0 0 0 [V ]
4 5, 4 5 [ A ]
I 2 nB
5 0 0 0 0 0 [V A ]
S nB
=
=
e2n
2 3 0 0 [V ]
2 1 7 , 3 9 [A ]
2
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
Osserviamo che le correnti nominali uguali (o quasi) a quelle misurate durante
la prova di corto circuito sono quelle relative al primario.
Questo significa che nella prova sono stati cortocircuitati i secondari e quindi le
grandezze misurate sono relative ai primari (cioè ai lati a 11000 V).
La rete equivalente semplificata corrispondente è riferita ai primari:
VC
ZccB
e1n
e1n
e2n
e2n
IC
carico
ZccA
3
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
Calcoliamo le impedenze di corto circuito riferite ai primari:
A
Z ccA
2 7 5 [V ]
V ccA
=
=
I n A m is
9, 2 [ A ]
R ccA
1 0 0 0 [W ]
PccA
= 2
=
I n A m is
9, 2 2  A 2 
X ccA =
2
2
Z ccA
− R ccA
=
2 9, 8 9 [ Ω ]
1 1, 8 1 [ Ω ]
2 9, 8 9 2 − 1 1, 8 1 2
2 7 , 4 6 [Ω ]
Z ccA = 1 1, 8 1 + j 2 7 , 4 6 [ Ω ]
4
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
B
Z ccB
3 4 5 [V ]
V ccB
=
=
I n B m is
4 5, 5 [ A ]
R ccB
3 3 7 0 [W ]
PccB
= 2
=
I n B m is
4 5, 5 2  A 2 
X ccB =
2
2
Z ccB
− R ccB
=
7 , 5 8 [Ω ]
1, 6 3 [ Ω ]
7 , 5 8 2 − 1, 6 3 2
7 , 4 0 [Ω ]
Z ccB = 1, 6 3 + j 7 , 4 0 [ Ω ]
5
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
Riportiamo le impedenze di corto circuito ai secondari, con il rapporto di
trasformazione:
1 1 0 0 0 [V ]
e1n
k =
=
e2n
2 3 0 0 [V ]
A
4, 7 8
R 2 ccA
1 1, 8 1 [ Ω ]
R ccA
=
=
2
k
4, 7 8 2
0, 5 1 7 [ Ω ]
X 2 ccA
2 7 , 4 6 [Ω ]
X ccA
=
=
2
k
4, 7 8 2
1, 2 0 0 [ Ω ]
Z 2 ccA = 0, 5 1 7 + j1, 2 0 0 [ Ω ]
6
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
B
R 2 ccB
R ccB 1, 6 3 [ Ω ]
=
=
2
k
4, 7 8 2
0, 0 7 1 [ Ω ]
X 2 ccB
7 , 4 0 [Ω ]
X ccB
=
=
2
k
4, 7 8 2
0, 3 2 4 [ Ω ]
Z 2 ccB = 0, 0 7 1 + j 0, 3 2 4 [ Ω ]
Calcoliamo ora il modulo e la fase di Z2ccA e Z2ccB:
A
Z 2 ccA =
Z 2 ccA
R 22 ccA + X 22 ccA =
 X 2 ccA 
= arctan 

 R 2 ccA 
0, 5 1 7 2 + 1, 2 0 0 2
1, 3 0 7 [ Ω ]
6 6, 7 °
7
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
Z 2 ccA = 1, 3 0 7 e j6 6 ,7 ° [ Ω ]
B
Z 2 ccB =
Z 2 ccB
R 22 ccB + X 22 ccB =
 X 2 ccB 
= arctan 

R
 2 ccB 
0, 0 7 1 2 + 0, 3 2 4 2
0, 3 3 1 [ Ω ]
77, 6°
Z 2 ccB = 0, 3 3 1e j7 7 ,6 ° [ Ω ]
8
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
A questo punto possiamo far riferimento a una rete equivalente semplificata
riferita ai secondari:
e1 n
e1 n
e2 n
e2 n
I2 A
VC
Z 2 ccB
I2 B
IC
carico
Z 2 ccA
9
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
Possiamo schematizzare la rete equivalente semplificata riferita ai secondari nel
seguente modo:
I2 B
I2 A
Z 2 ccB
carico
Z 2 ccA
IC
e2 n
VC
e2 n
IC = I C ( co s ϕ carico − j sin ϕ carico ) = I C ( 0, 8 − j 0, 6 ) = I C e − j3 6 ,8 7 °
10
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
Calcoliamo l’impedenza equivalente al parallelo delle impedenze dei due
trasformatori:
IC
carico
Z eq
Z eq
VC
Z 2 ccA ∗ Z 2 ccB
=
Z 2 ccA + Z 2 ccB
e2 n
IC = I C ( co s ϕ carico − j sin ϕ carico ) = I C ( 0, 8 − j 0, 6 ) = I C e − j3 6 ,8 7 °
11
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
Calcoliamo prima separatamente numeratore e denominatore di:
Z eq
Z 2 ccA ∗ Z 2 ccB
=
Z 2 ccA + Z 2 ccB
Z 2 ccA ∗ Z 2 ccB = 1, 3 0 7 ∗ 0, 3 3 1 = 0, 4 3 3 [ Ω ]
(Z
2 ccA
∗ Z 2 ccB ) = 6 6, 7 ° + 7 7 , 6 ° = 1 4 4, 3 °
numeratore
denominatore
R e ( Z 2 ccA + Z 2 ccB ) = R 2 ccA + R 2 ccB = 0, 517 + 0, 071 = 0, 588 [ Ω ]
Im ( Z 2 ccA + Z 2 ccB ) = X 2 ccA + X 2 ccB = 1, 200 + 0, 324 = 1, 524 [ Ω ]
Z 2 ccA + Z 2 ccB =
0, 5 8 8 2 + 1, 5 2 4 2 = 1, 6 3 4 [ Ω ]
 1, 5 2 4 
Z
+
Z
=
arctan
( 2 ccA 2 ccB )
 0, 5 8 8 


6 8, 9 °
12
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
Z eq =
0, 4 3 3
= 0, 2 6 5 [ Ω ]
1, 6 3 4
Z eq = 1 4 4, 3 ° − 6 8, 9 ° = 7 5, 4 °
Z eq = 0, 2 6 5e j7 5 , 4 ° [ Ω ]
R e ( Z eq ) = 0, 265 cos ( 75, 4 ° ) = 0, 067 [ Ω ]
Im ( Z eq ) = 0, 265 sin ( 75, 4 ° ) = 0, 257 [ Ω ]
Z eq = 0, 0 6 7 + j 0, 2 5 7 [ Ω ]
13
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
Riprendiamo il circuito equivalente, fissiamo ad arbitrio la fase della tensione
sul carico pari a 0° e calcoliamo la fase ϕ della tensione e 2 n
IC = I C e − j3 6 ,8 7 °
carico
Z eq = 0, 2 6 5e j7 5 , 4 °
V C = 2 2 5 0 e j0 °
e 2 n = 2 3 0 0 e jϕ
Scriviamo l’equazione alla maglia:
2 3 0 0 e j ϕ − 0, 2 6 5 I C e
e 2 n − Z eq IC = V C
j ( 7 5 , 4 − 3 6 ,8 7 )°
= 2 2 5 0 e j0 °
2 3 0 0 e j ϕ − 0, 2 6 5 I C e j3 8 ,5 4 ° = 2 2 5 0 e j0 °
14
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
L’equazione alla maglia:
2 3 0 0 e j ϕ − 0, 2 6 5 I C e j3 8 ,5 4 ° = 2 2 5 0 e j0 °
è un’equazione vettoriale, pertanto può essere scomposta in due equazioni
scalari ed è risolubile nelle due incognite ϕ e IC :
2 3 0 0 co s ϕ − 0, 2 6 5 I C co s ( 3 8, 5 4 ° ) = 2 2 5 0
2 3 0 0 sin ϕ − 0, 2 6 5 I C sin ( 3 8, 5 4 ° ) = 0
Nell’ipotesi di ϕ molto piccolo, avremo:
(soluzione approssimata)
co s ϕ = 1
sin ϕ = ϕ
2 3 0 0 − 0, 2 6 5 I C co s ( 3 8, 5 4 ° ) = 2 2 5 0
2 3 0 0 ϕ − 0, 2 6 5 I C sin ( 3 8, 5 4 ° ) = 0
15
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
2300 − 2250
IC =
0, 2 6 5 co s ( 3 8, 5 4 ° )
ϕ=
2 4 1, 0 4 [ A ]
0, 2 6 5 ∗ 2 4 1, 0 4 ∗ sin ( 3 8, 5 4 ° )
2300
0, 0 1 7 [ rad ]
0, 9 9 2 °
Osserviamo che l’ipotesi di ϕ molto piccolo è verificata.
La soluzione rigorosa si ottiene nel seguente modo:
2 3 0 0 e j ϕ = 0, 2 6 5 I C e j3 8 ,5 4 ° + 2 2 5 0 e j0 °
2300 ( cos ϕ + j sin ϕ ) = 0, 265I C ( cos 38, 54 + j sin 38, 54 ) + 2250
2 3 0 0 ( co s ϕ + j sin ϕ ) = ( 0, 2 0 7 I C + 2 2 5 0 ) + j0,1 6 5 I C
16
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
Passando ai moduli:
2 3 0 0 2 = 0, 0 4 3I C2 + 2 2 5 0 2 + 9 3 3, 5 I C + 0, 0 2 7 I C2
0, 0 7 I C2 + 9 3 3, 5 I C − 2 2 7 5 0 0 = 0
IC =
IC =
−b ±
b 2 − 4ac
− 933, 5 ±
=
2a
− 933, 5 ±
933, 5 2 + 4 ∗ 0, 07 ∗ 227500
=
2 * 0, 07
933, 5 2 + 4 ∗ 0, 07 ∗ 227500
− 933, 5 ± 967,1
=
=
2 * 0, 07
0,14
+ 240, 5 [A ]
(il valore corretto è quello positivo, perché è un modulo)
IC =
− 13575, 6 [A ]
17
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
Per calcolare ϕ considero la parte immaginaria dell’equazione:
2 3 0 0 ( co s ϕ + j sin ϕ ) = ( 0, 2 0 7 I C + 2 2 5 0 ) + j0,1 6 5 I C
2 3 0 0 sin ϕ = 0,1 6 5 I C
sin ϕ =
0,1 6 5 ∗ 2 4 0, 5
= 0, 0 1 7 2
2300
ϕ = 0, 9 9 0 °
In questo caso i risultati ottenuti con la soluzione rigorosa sono quasi identici a
quelli ottenuti con la soluzione approssimata, perché in effetti ϕ è molto piccolo.
18
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
A questo punto possiamo calcolare la potenza fornita dai due trasformatori:
A = IC V C = 2 4 0, 5e − j3 6 ,8 7 ° ∗ 2 2 5 0 e j0 °
5 4 1e − j3 6 ,8 7 ° [ k V A ]
Ora dovremmo verificare quale è la potenza fornita da ciascuno dei due
trasformatori.
Prima calcoliamo la corrente fornita da ciascun trasformatore:
I2 A =
Z eq IC
Z 2 ccA
I2 A =
I2 B =
I2 B =
Z eq IC
Z 2 ccB
0, 2 6 5
7 5, 4 ° i 2 4 0, 5 − 3 6, 8 7 °
= 4 8, 8 1
1, 3 0 7 6 6, 7 °
0, 2 6 5
7 5, 4 ° i 2 4 0, 5 − 3 6, 8 7 °
= 1 9 2, 4 1
0, 3 3 1 7 7 , 6 °
− 2 8,1 8 ° A
− 3 9, 0 7 ° A
19
Esercitazioni sul trasformatore
FUNZIONAMENTO IN PARALLELO DI DUE TRASFORMATORI
Si osserva che la somma dei moduli delle correnti nei due trasformatori è
maggiore del modulo della corrente nel carico. Questo accade perché la corrente
nel carico è data dalla somma vettoriale delle correnti nei due trasformatori, le
quali hanno fase diversa l’una dall’altra.
Il grado di carico dei due trasformatori è:
αA
I2 A
4 8, 8 1
=
=
≅ 1,1 2
I2 A n
4 3, 4 8
αB
I2 B
1 9 2, 4 1
=
=
≅ 0, 8 9
I2 B n
217, 39
il trasformatore A è sovraccaricato
La potenza fornita da ciascun trasformatore è:
A A = V C I2 A = 2 2 5 0
0 ° i 4 8, 8 1
− 2 8, 8 1 °
A A ≅ 110 kV A
A B = V C I2 B = 2 2 5 0
0 ° i1 9 2, 4 1
− 3 9, 0 7
A B ≅ 433 kV A
20