Multipli e sottomultipli. Divisibilità

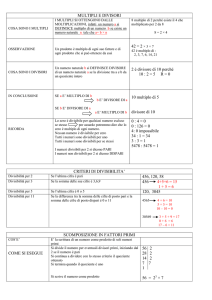
1 Multipli e sottomultipli. Divisibilità
LA TEORIA
Se la divisione fra due numeri naturali è propria (cioè il resto è uguale a 0) i due numeri si
dicono divisibili. Per esempio, nella divisione 18 : 3 diciamo che 18 è divisibile per 3.
Se due numeri naturali a e b sono divisibili, si definisce il numero a multiplo di b e il numero b sottomultiplo o divisore di a.
I multipli di un numero si ottengono moltiplicandolo per ogni numero della successione
dei numeri naturali 0, 1, 2, 3, 4, 5…
Ogni numero naturale diverso da zero ha infiniti multipli.
Per esempio l’insieme M (7) dei multipli di 7 è:
M ​( 7 )​ = {​  7 × 0; 7 × 1; 7 × 2; 7 × 3; 7 × 4; 7 × 5… }​ = {​  0; 7; 14; 21; 28; 35… }​
L’insieme dei divisori di un numero è un insieme finito formato da tutti i numeri, compreso
il numero stesso e il numero 1, per i quali è divisibile il numero di partenza.
Per esempio, l’insieme D {16} dei divisori di 16 è:
D (​ 16 )​ = {​  1; 2; 4; 8; 16 }​
Un numero naturale maggiore di 1, divisibile solo per 1 e per se stesso, si dice numero
primo:
7, 11, 19 sono numeri primi
Un numero naturale che non è primo si dice numero composto:
6, 35, 81 sono numeri composti
Due numeri naturali che hanno come divisore comune soltanto il numero 1 si dicono primi fra loro:
3 e 8 sono primi fra loro
GLI ESERCIZI
1 Sostituisci ai puntini le espressioni “è divisore di” o “è divisibile per”:
è divisore di
.......................................................................... 744
22
è divisore di
1452
è
divisore
di
è
divisibile
per
24 .......................................................................... 216 2000 .................................................................... 40
è divisibile per
è divisore di
60 450 ....................................................................
2700
7440 ..........................................................................
124
.................................................................... 2 Scrivi l’insieme dei primi 5 multipli dei seguenti numeri:
{0, 12, 24, 36, 48}
12 → M (12) = ......................................................................................................................................................................
M (7) = {0, 7, 14, 21, 28}
7 → .............................................................................................................................................................................................
M (11) = {0, 11, 22, 33, 44}
11 → .............................................................................................................................................................................................
M (4) = {0, 4, 8, 12, 16}
4 → .............................................................................................................................................................................................
M (9) = {0, 9, 18, 27, 36}
9 → .............................................................................................................................................................................................
58
Unità
5
MULTIPLI E SOTTOMULTIPLI
M.C.D. e m.c.m.
3 Indica con una crocetta il completamento corretto:
D (24) =
{1; 2; 3; 4; 6; 8; 12; 24}
{2; 4; 6; 8; 12; 24}
✗ {3; 6; 8; 12}
D (12) =
{1; 12}
✗ {1; 2; 3; 4; 6; 12}
{2; 4; 6; 8; 10; 12}
D (15) =
{3; 5; 15}
✗ {1; 3; 5; 15}
{1; 3; 5; 15; 9; 18}
4 Scrivi l’insieme dei divisori dei seguenti numeri:
{1, 2, 4, 8, 16, 32}
32 → D (32) = ............................................................
D (18) = {1, 2, 3, 6, 9, 18}
18 → ...................................................................................
D (42) = {1, 2, 3, 6, 7, 14, 21, 42}
42 → ...................................................................................
D (12) = {1, 2, 3, 4, 6, 12}
12 → ...................................................................................
D (6) = {1, 2, 3, 6}
6 → ...................................................................................
D (26) = {1, 2, 13, 26}
26 → ...................................................................................
5 Scrivi tutti i multipli di 9 compresi tra 10 e 30:
18 27
................................................................................................................................................................................................................
6 Scrivi tutti i numeri primi minori di 44:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43
................................................................................................................................................................................................................
7 Indica tra i seguenti numeri quali sono primi e quali composti:
152
composto
composto
.........................................................................................
144
........................................................................................
13
primo
primo
......................................................................................... 19 ........................................................................................
26
composto
......................................................................................... 41 primo
........................................................................................
8 Indica quali fra le seguenti coppie sono costituite da numeri primi fra loro:
3; 30
10; 100
4; 30
8; 64
7; 61
✗
13; 5
15; 120
✗
88; 66
59
2 Criteri di divisibilità
LA TEORIA
I criteri di divisibilità sono regole che ci permettono di stabilire, senza effettuare la
divisione, se un numero è divisibile per un altro.
Criterio di divisibilità per 2
Un numero è divisibile per 2 se la sua ultima cifra a destra è zero oppure una cifra pari.
Criterio di divisibilità per 3
Un numero è divisibile per 3 se la somma delle sue cifre è 3 oppure un multiplo di 3.
Criterio di divisibilità per 5
Un numero è divisibile per 5 se la sua ultima cifra a destra è zero oppure 5.
Criterio di divisibilità per 11
Un numero è divisibile per 11 se la differenza tra la somma delle sue cifre di posto dispari
e quella delle sue cifre di posto pari è 0 o 11 o un multiplo di 11.
1° 2° 3° 4° 5° Somma cifre posto pari
Somma cifre posto dispari
8 0 9 1 6
0 + 1 = 1
8 + 9 + 6 = 23
23 - 1 = 22 (è multiplo di 11)
GLI ESERCIZI
1 Indica con una crocetta quali fra i seguenti numeri sono divisibili per 2:
34
........................................................... ✗ 5248
............................................................. ✗
127
........................................................... 304
............................................................. ✗
2 Indica con una crocetta quali fra i seguenti numeri sono divisibili per 3:
81
........................................................... 536
........................................................... ✗ 215
............................................................. 3222
............................................................. ✗
3 Indica con una crocetta quali fra i seguenti numeri sono divisibili per 11:
121
........................................................... 651
........................................................... ✗
13 258 ............................................................. 968
............................................................. ✗
4 Scrivi tre numeri divisibili per 2, tre numeri divisibili per 3, tre numeri divisibili per 5 e tre numeri divisibili per 11:
divisibili per 2: 70 806 1024
................................................................................................................................................................................................................
divisibili per 3: 54 162 3216
................................................................................................................................................................................................................
divisibili per 5: 45 160 1235
................................................................................................................................................................................................................
divisibili per 11: 242 506 1331
................................................................................................................................................................................................................
60
3 Scomposizione
in fattori primi
LA TEORIA
Unità
5
MULTIPLI E SOTTOMULTIPLI
M.C.D. e m.c.m.
L’operazione che trasforma un numero composto nel prodotto di fattori primi è detta
scomposizione in fattori primi. Per esempio:
18 = 3 × 3 × 2
Per scomporre un numero in fattori primi occorre procedere come segue:
• Scriviamo il numero 156 e alla sua destra tracciamo una riga verticale.
156
•Scriviamo a destra della riga il più piccolo numero primo che sia divisore di 156 (in questo caso 2) e il quoto (78) sotto il numero 156.
1562
78
•Scriviamo a destra di 78 il più piccolo numero primo che sia un suo
divisore (ancora 2) e il quoto 39 sotto il numero 78.
1562
78 2
39
•Scriviamo a destra di 39 il più piccolo numero che sia un suo divisore
(3) e il quoto 13 sotto il numero 39.
1562
78 2
39 3
13 13
•Il numero 13 è un numero primo, quindi il più piccolo numero primo
che sia un suo divisore è proprio 13. Scriviamo 13 nella colonna di destra e il quoto 1 nella colonna di sinistra.
1562
78 2
39 3
13 13
1
•Quando si arriva al numero 1 il processo di scomposizione si arresta.
A questo punto è possibile scrivere il numero come prodotto di tutti i
numeri primi scritti a destra della riga:
156 = 2 × 2 × 3 × 13 = 22 × 3 × 13
GLI ESERCIZI
1 Scomponi in fattori primi i seguenti numeri:
2224 2
4624 2
2312 2
1112 2
1156 2
556 2
578 2
278 2
289 17
139 139
17 17
1
1
8
4
4
2
2
×
3
×
592
×
1392
× 172
256 = ........................354 = ........................2224 = ........................4624 = ........................
256 2
128
64
32
16
8
4
2
1
2
2
2
2
2
2
2
354 2
177 3
59 59
1
61
Comune Divisore (M.C.D.)
4 Massimo
e minimo comune multiplo (m.c.m.)
LA TEORIA
Il Massimo Comune Divisore (M.C.D.) di due o più numeri è il maggiore dei loro divisori comuni.
Il minimo comune multiplo (m.c.m.) di due o più numeri è il minore dei loro multipli comuni, escluso lo zero.
Ricerca del M.C.D.
Consideriamo i numeri 9 e 12. Per calcolare il M.C.D. scriviamo tutti i divisori dei due
numeri:
D (9) = {​ 1; 3; 9 }​ D (12) = ​{ 1; 2; 3; 4; 6; 12 }​
Il M.C.D. è il divisore comune più grande:
M.C.D. (9, 12) = 3
Ricerca del m.c.m.
Per calcolare il m.c.m. scriviamo tutti i multipli dei due numeri escluso lo zero:
M (9) = {​ 9; 18; 27; 36… }​ M (12) = ​{ 12; 24; 36… }​
Il m.c.m. è il multiplo comune più piccolo:
m.c.m. (9, 12) = 36
Consideriamo i numeri 180 e 232. Scomponiamoli in fattori primi:
1802
90 2
45 3
15 3
5 5
1
180 = 22 × 32 × 5
2322
116 2
58 2
29 29
1
232 = 23 × 29
Per calcolare il M.C.D. consideriamo i fattori primi comuni presi una sola volta con il minimo esponente. Nel nostro caso:
22 → M.C.D. (180, 232) = 4
Per calcolare il m.c.m. prendiamo i fattori primi comuni e non comuni una sola volta con
il massimo esponente:
440 m.c.m. (180, 232) = 10 440
23 × 32 × 5 × 29 = 10 GLI ESERCIZI
1 Calcola il M.C.D. e il m.c.m. dei numeri 25 e 35:
{1, 5, 25}
D (25) = ...............................................................................
{1, 5, 7, 35}
5
D (35) = ...............................................................................
M.C.D. = ...............................................................................
{25, 50, 75, 100, 125, 150, 175, …}
M (25) = ..............................................................................
{35, 70, 105, 140, 175, …}
175
M (35) = ..............................................................................
m.c.m. = ..............................................................................
62
Unità
5
MULTIPLI E SOTTOMULTIPLI
M.C.D. e m.c.m.
2 Calcola il M.C.D. e il m.c.m. dei numeri 6, 12 e 16:
D (6) =
{1, 2, 3, 6}
..................................................................................
{1, 2, 3, 4, 6, 12}
D (12) =
...............................................................................
D (16) =
...............................................................................
M (6) =
{1, 2, 4, 8, 16}
2
M.C.D. =
...............................................................................
m.c.m. =
..............................................................................
{6, 12, 18, 24, 30, 36, 42, 48, …}
.................................................................................
{12, 24, 36, 48, …}
M (12) = ..............................................................................
{16, 32, 48, …}
M (16) = ..............................................................................
48
3 Calcola il M.C.D. e il m.c.m. dei numeri 30, 60, 90 con il metodo della scomposizione in fattori
primi:
30 2
15 3
5 5
1
m.c.D. =
60 2
30 2
15 3
5 5
1
90
45
15
5
1
2
3
3
5
2 × 3 × 5 = 302
× 3 × 5 = 180
...............................................................................
m.c.m. = ..............................................................................
2
2
4 Calcola il M.C.D. e il m.c.m. dei numeri 26, 42, 86 con il metodo della scomposizione in fattori
primi:
26 2
13 13
1
m.c.D. =
42 2
21 3
7 7
1
86
43
1
2
43
22
× 3 × 7 × 13 × 43 = 23 478
m.c.m. = ..............................................................................
...............................................................................
5 Calcola il M.C.D. e il m.c.m. dei numeri 46, 58, 62 con il metodo della scomposizione in fattori
primi:
46 2
23 23
1
m.c.D. =
58 2
29 29
1
62
31
1
2
31
22
× 23 × 29 × 31 = 41354
...............................................................................
m.c.m. = ..............................................................................
63
Comune Divisore (M.C.D.)
4 Massimo
e minimo comune multiplo (m.c.m.)
6 Calcola il M.C.D. e il m.c.m. dei numeri 40, 120, 126:
40 2
20 2
10 2
5 5
1
120 2
60 2
30 2
15 3
5 5
1
126
63
21
7
1
2
3
3
7
3
× 32 × 5 × 7 = 2520
22
m.c.D. = ...............................................................................
m.c.m. = ..............................................................................
7 Calcola il M.C.D. e il m.c.m. dei numeri 132, 154, 218:
132 2
66 2
33 3
11 11
1
154 2
77 7
11 11
1
218
109
1
2
109
2
22
× 3 × 7 × 11 × 109 = 100 716
m.c.D. = ...............................................................................
m.c.m. = ..............................................................................
8 Inserisci al posto dei puntini un numero in modo da rendere vera l’uguaglianza:
12 ; 27) = 3
M.C.D. (9; ............
21 ; 28) = 7
M.C.D. (............
23 ; 25) = 1
M.C.D. (............
35 ; 50) = 5
M.C.D. (15; ............
20 ; 25) = 5
M.C.D. (15; ............
10 ; 12) = 2
M.C.D. (6; ............
9 Inserisci al posto dei puntini un numero in modo da rendere vera l’uguaglianza:
m.c.m. (5;
4 ; 6; 12) = 12
m.c.m. (............
16 ) = 48
m.c.m. (6; 8; ............
m.c.m. (4;
64
6 )
............
12 ) = 24
m.c.m. (8; ............
6
............;
16) = 48
m.c.m. (2;
8
............;
= 30
11) = 88
Unità
5
L'angolo
del problema
1 Un editore pubblica a dispense settimanali tre romanzi che avranno rispettivamente 192,
160 e 200 pagine. L’editore vuole che le pagine delle dispense dei tre volumi siano di uguale numero e che questo sia il massimo possibile. Da quante pagine deve essere formata
ogni dispensa e da quanti fascicoli sarà composto ciascun romanzo?
Ti do una mano...
Per determinare il numero delle pagine che dovrà avere ogni dispensa occorre calcolare il
M.C.D. tra le pagine complessive dei tre romanzi:
192 2
96 2
48 2
24 2
12 2
6 2
3 3
1
160 2
80 2
40 2
20 2
10 2
5 5
1
200
100
50
25
5
1
2
2
2
5
5
8
che corrisponde al numero delle pagine che dovrà avere ogni diIl M.C.D. è ........................
spensa.
Per sapere da quanti fascicoli sarà composto ogni romanzo occorre dividere �������������������������������
192 : 8 = 24 160 : 8 = 20 200 : 8 = 25
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
[8; 24; 20; 25]
2 Tre percorsi stradali sono lunghi rispettivamente 33 km, 88 km e 55 km. Si vogliono disporre
dei cartelli pubblicitari alla massima distanza possibile l’uno dall’altro, ma a distanze uguali
in ciascuno dei percorsi.
A che distanza l’uno dall’altro verranno posti i cartelli? Quanti ne occorreranno se ne verrà
messo uno all’inizio di ogni percorso?
Prova da solo!
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
M.C.D. (33, 88, 55) = 11
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
4 + 9 + 6 = 19
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
[11 km; 19]
65