Lezione in PDF

LA CORRENTE ALTERNATA
LA LEZIONE
La risposta dei singoli elementi circuitali ideali alla corrente alternata
Una semplice bobina (un filo conduttore avvolto a spirale su un cilindro di materiale
isolante) non può essere considerata un induttore ideale. Essa è caratterizzata da una
resistenza e da un’induttanza e solo il termine capacitivo può, in genere, essere
trascurato rispetto agli altri due, almeno per le frequenze caratteristiche della rete
elettrica. In determinate condizioni è possibile approssimare le proprietà elettriche di
elementi circuitali a pure resistenze R, induttanze L o capacità C. L’analisi della risposta
a grandezze alternate degli elementi circuitali ideali è ricondotta a metodi matematici
avanzati oppure è affrontata con un attrezzato laboratorio di elettronica. Qui
utilizzeremo un programma di simulazione gratuito che permette la costruzione di
circuiti e la misura delle grandezze in gioco al variare del tempo.
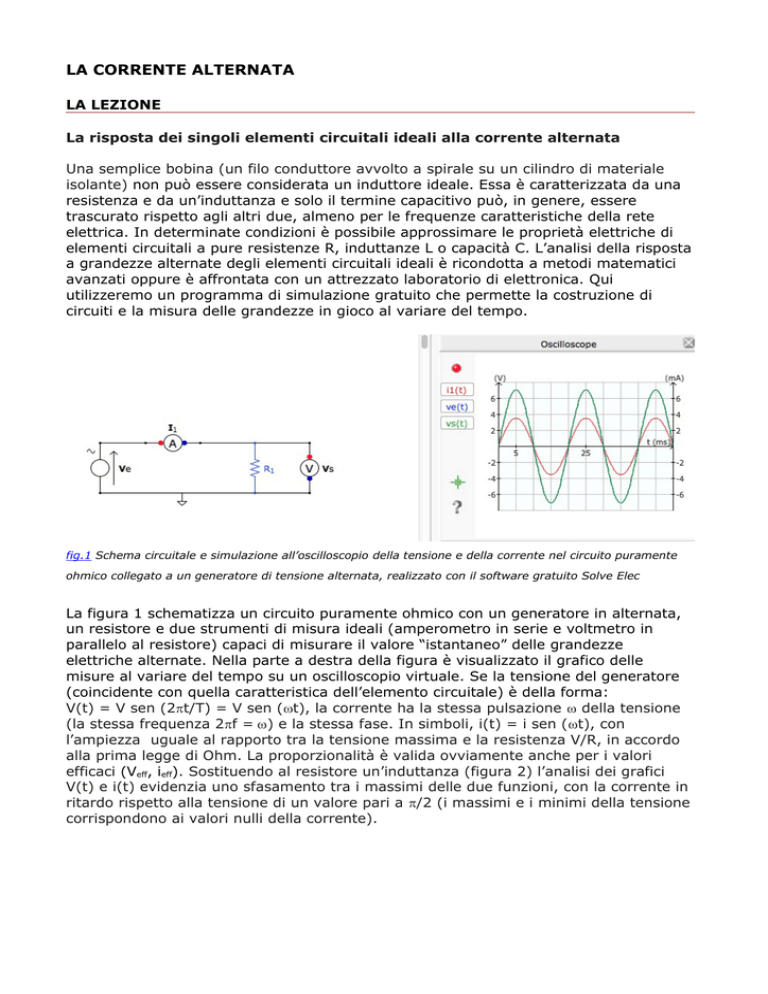
fig.1 Schema circuitale e simulazione all’oscilloscopio della tensione e della corrente nel circuito puramente
ohmico collegato a un generatore di tensione alternata, realizzato con il software gratuito Solve Elec
La figura 1 schematizza un circuito puramente ohmico con un generatore in alternata,
un resistore e due strumenti di misura ideali (amperometro in serie e voltmetro in
parallelo al resistore) capaci di misurare il valore “istantaneo” delle grandezze
elettriche alternate. Nella parte a destra della figura è visualizzato il grafico delle
misure al variare del tempo su un oscilloscopio virtuale. Se la tensione del generatore
(coincidente con quella caratteristica dell’elemento circuitale) è della forma:
V(t) = V sen (2t/T) = V sen (wt), la corrente ha la stessa pulsazione w della tensione
(la stessa frequenza 2f = w) e la stessa fase. In simboli, i(t) = i sen (wt), con
l’ampiezza uguale al rapporto tra la tensione massima e la resistenza V/R, in accordo
alla prima legge di Ohm. La proporzionalità è valida ovviamente anche per i valori
efficaci (Veff, ieff). Sostituendo al resistore un’induttanza (figura 2) l’analisi dei grafici
V(t) e i(t) evidenzia uno sfasamento tra i massimi delle due funzioni, con la corrente in
ritardo rispetto alla tensione di un valore pari a /2 (i massimi e i minimi della tensione
corrispondono ai valori nulli della corrente).
fig.2 Schema circuitale e simulazione della tensione e della corrente in un circuito puramente
induttivo realizzato con il software gratuito Solve Elec
Ora i(t) = i sen (wt-/2), con l’ampiezza i = V/ wL, dove il termine wL è il fattore di
scala equivalente alla resistenza nel caso precedente. La stessa espressione può essere
scritta nella forma: i(t) = -i cos (wt).
Infine esaminando un condensatore in alternata (figura 3) si trova che la corrente è in
anticipo rispetto alla tensione di un fattore di fase /2 (i massimi sono raggiunti prima
dalla corrente e poi dalla tensione). La corrente nel tempo assume la forma:
i(t) = wCV sen (wt+/2)= wCV cos (wt). Il nuovo termine, avente la stessa unità della
resistenza è allora: 1/wC.
fig.3 Schema circuitale e simulazione della tensione e della corrente in un circuito puramente capacitivo
realizzato con il software gratuito Solve Elec
Il circuito RL
Collegando una bobina a una pila di tensione V, la corrente continua non raggiunge
istantaneamente (vedi figura 4) il valore di equilibrio i=V/R.
fig.4 Risposta di una
induttanza alla
tensione continua. La
curva della tensione
rispetto al tempo è
una funzione
esponenziale
crescente
Il tempo caratteristico di rilassamento t dipende dai valori di resistenza e induttanza
della bobina (t=L/R). Così è facile convincersi che aumentando l’induttanza (ad
esempio inserendo un ferro nella bobina) la curva esponenziale ha un tempo
caratteristico più lungo.
La risposta della bobina a una tensione alternata può essere considerata la
sovrapposizione della soluzione dell’equazione differenziale omogenea associata e di
una soluzione particolare. Se si abbina il transitorio iniziale (che adesso può essere di
forma esponenziale o di oscillazione smorzata) la risposta è ancora una funzione
sinusoidale che ha uguale frequenza f rispetto alla tensione, ma diversa ampiezza
i=V/Z (con impedenza Z = [R2+(wL)2]1/2, come abbiamo già ricordato nelle precedenti
lezioni). E sfasamento  rispetto alla causa: i(t)=i sen (wt-). Il valore dello sfasamento
può variare tra zero e /2, a seconda della predominanza nel calcolo dell’impedenza del
termine resistivo (R>> wL, =0) oppure del termine induttivo (wL>>R, =/2). Lo
studio della dipendenza dello sfasamento dal rapporto wL/R porta alla funzione
rappresentata in figura 5.
fig.5 Dipendenza dello
sfasamento dal rapporto ωL/R
in un circuito RL
In essa ad esempio già per wL/R=4 (facilmente realizzabile con le bobine dei
trasformatori con nucleo in ferro) =1,326 rad, valore non lontanissimo dal limite /2
ottenibile per un elemento puramente induttivo.
La bobina saltatrice
Inserendo una bobina nel giogo in ferro a forma di U e collegandola alla tensione di
rete non si hanno intensi effetti meccanici. Se però si dispone la bobina con un singolo
ferro a forma di parallelepipedo (figura 6) si osserva un innalzamento della bobina, una
rapida serie di oscillazioni e infine una stabilizzazione a una certa altezza, dove vi è
equilibrio tra la forza di Lorentz e la forza di gravità.
fig.6 Dispositivo
sperimentale per lo studio
delle oscillazioni della
bobina
L’analisi delle oscillazioni smorzate (figura 7) della bobina (che traduce il transiente
delle grandezze elettriche in variazioni di grandezze meccaniche) è da fondare sulla
legge di Faraday-Neumann-Lenz dell’induzione: la variazione temporale del flusso
d’induzione magnetica produce una forza elettromotrice indotta (fem=- Dt).
fig.7 Esempio di oscillazione smorzata
Il campo magnetico verticale, perpendicolare agli avvolgimenti della bobina, determina
una variazione di flusso proporzionale alla corrente i, Li. La componente radiale del
campo è la causa della forza di Lorentz perpendicolare sia alla corrente che al campo
(si veda l’esempio dell’anello di Thomson nella lezione dell’induzione). Le correnti
autoindotte nella bobina tendono a limitare le variazioni del flusso. La levitazione verso
il centro del ferro della bobina innalza il valore del coefficiente di autoinduzione (come
abbiamo già osservato nella lezione precedente) rispetto alla posizione iniziale. Il punto
chiave è però ancora lo sfasamento delle grandezze elettriche.
Per capirlo conviene modificare l’apparato
sperimentale utilizzando non una, ma due bobine.
La prima fissa collegata alla rete elettrica, la
seconda mobile collegata a un insieme di
condensatori e accoppiata alla prima tramite
materiale ferromagnetico (figura 8). In questo
modo il secondario, dove si sviluppano correnti
indotte, è un circuito RCL i cui valori possono
essere controllati.
fig.8 Schema elettrico dell’esperimento con le due bobine
Fasi attrattive e repulsive: un circuito RLC
Nell’esperimento descritto nelle Harvard Natural Sciences Lecture Demonstrations, si
veda la figura 9, il movimento, dovuto alla forza di Lorentz, della seconda bobina può
essere sia attrattivo che repulsivo a seconda dei valori della capacità dei condensatori.
fig.9 Foto dell’esperimento con le due
bobine
Immaginiamo due fili percorsi da corrente continua: se i versi sono concordi vi è
attrazione, se i versi sono discordi vi è repulsione. Nel caso della corrente alternata è
possibile che in media l’attrazione compensi la repulsione. La risonanza del sistema
elettrico si ha proprio quando la media della forza di Lorentz è uguale a zero, in tal
caso anche la seconda bobina è ferma e gli effetti induttivi sono compensati dagli effetti
capacitivi. Ritornando alle espressioni dei circuiti ideali se la fem=V sen(wt),
iL=-i cos(wt) con i=-V/wL, iC=i cos(wt) con i= wCV, iR=i sen(wt) con i=V/R e l’impedenza
del circuiro RLC risulta Z= [(-wL+1/wC)2+ R2]1/2.
La risonanza del circuito RLC serie si ottiene nell’esperimento modificando C (w è
costante) in modo da avere Z=R. Il circuito puramente ohmico si ottiene per wL=1/wC,
ovvero C=1/wL. In tal caso la forza elettromotrice indotta (tensione) nella seconda
bobina e la corrente indotta sono in fase. Il flusso d’induzione e quindi la corrente di
rete nella prima bobina è sfasata di /2 rispetto alla corrente nella seconda bobina. La
rappresentazione delle grandezze elettriche in funzione dell’angolo estesa a un ciclo è
riportata nella figura 10.
In essa è evidente che la forza di
Lorentz attrattiva e repulsiva è
egualmente ripartita in modo che il
valore medio è esattamente uguale a
zero.
Un secondo caso limite è quello in cui
la corrente nella seconda bobina
rimane sempre opposta a quella nella
prima bobina, allora l’induttanza
domina rispetto alla capacità e alla
resistenza, la forza di Lorentz è sempre
negativa in tutti i punti del ciclo e la
seconda bobina subisce una forza
repulsiva massima.
Fig.10 Grandezze alternate nel circuito
puramente resistivo
Forza elettromotrice e corrente indotta
sono sfasate di /2, mentre la corrente di
rete nella prima bobina e la corrente
indotta nella seconda sono sempre in
opposizione di fase (figura 11).
fig.11 Grandezze alternate che portano al caso di
repulsione massima tra le due bobine
Infine è possibile variare C fino ad
ottenere il massimo di una forza di
Lorentz attrattiva tra le due bobine. Il
caso limite (figura 12) corrisponde al
flusso di induzione in fase con la
corrente indotta e quindi a una pura
capacità dove la corrente è in anticipo
di /2 rispetto alla tensione (forza
elettromotrice).
fig.12 Grandezze alternate che portano al
massimo dell’attrazione tra le due bobine
Rispetto al caso dell’anello di Thomson dove prevale sempre l’aspetto induttivo, qui è
evidente che attrazione e repulsione sono due possibilità del circuito RLC secondario.
Se domina C, rispetto alle altre grandezze, la seconda bobina viene attratta dalla
prima; se prevale L, la seconda bobina si allontana dalla prima; infine se il circuito è
puramente resistivo, la bobina resta ferma. Gli effetti elettrici determinano movimenti
meccanici e la risonanza elettrica corrisponde in questo strano RLC al perfetto
equilibrio.