Capitolo 5
Funzioni. Grafici.
Definizione:
Una funzione f di una variabile reale, x , è una corrispondenza che associa ad ogni numero
reale x appartenente ad un insieme Df ⊆ R un unico numero reale, y ∈ R, denotato con f(x) che
si chiama immagine del punto x secondo la funzione f. L'insieme di tutti i valori assunti dalla
funzione f quando x varia nell'insieme Df si chiama immagine della funzione e si denota con
f( Df )
Df ≡ dominio o insieme di definizione della funzione f.
f : x ∈ Df ⊆ R → un solo y = f(x) ∈ f(Df) ⊆ R
x = valore di ingresso, variabile indipendente
f(x) = valore di uscita, variabile dipendente
Esempi:
f : x ∈ R → y = f(x) = mx + q retta funzione lineare in quanto la variabile x compare alla prima
potenza , l'insieme immagine è ancora tutto R
1
f : x ∈ R - {0} → y =
(iperbole) , Df = R - {0} e così pure l'insieme immagine f(Df)
x
Le coppie [x , f(x)] individuano punti nel piano cartesiano, in questo modo si costruisce il
grafico della funzione f.
Grafici della retta
m>0
m<0
Grafico dell’iperbole
y = f(x) =
y
1
x
1
2
2
x,x≥0
y = f(x) = |x | =
-x , x < 0
funzione valore assoluto
y
Il dominio è tutto R
L'insieme immagine è R+
1
-1
1
x
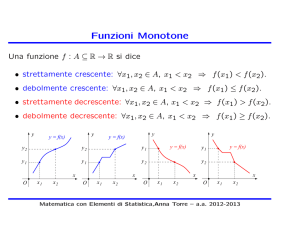
Funzioni Monotone
f(x) crescente: x1 ≤ x2
f(x) decrescente: x1 ≤ x2
⇒
⇒
f(x1) ≤ f(x2) (< strettamente crescente)
f(x1) ≥ f(x2) (< strettamente decrescente)
Negli esempi fatti
y = mx +q, m < 0, f è strettamente decrescente, m>0 strettamente crescente
y=
1
è strettamente decrescente per x > 0 e strettamente crescente per x < 0
x
y = |x |,
f è strettamente crescente per x ≥ 0 e strettamente decrescente per x <0
Funzioni elementari
(le più comuni funzioni di una variabile reale)
Funzione potenza con esponente n ∈ N
y = f(x) = xn
n = 2 f(x) = x2 (parabola)
n = 3 f(x) = x3 (cubica)
(n≠1, xn non lineare, es. f(x)=x2 ⇒ f(x1+x2) = x12 +x22 + 2x1x2 ≠ f(x1)+f(x2 )= x12 + x22 )
f( x) = x2 strettamente crescente per x ≥ 0,
strettamente decrescente per x < 0
Df = R , l'immagine=R+
f(x) = x3 strettamente crescente per x ∈ R ,
Df = R , l'immagine=R
Funzione potenza con esponente razionale f(x) = xm/n con m,n ∈ N.
Nota: se n è un intero dispari allora xm/n è definita anche per x < 0, se n è pari allora il
dominio di f è solo R+ cioè x ≥ 0.
Esempi : (-1)5/3 = 3 (−1) 5 = 3 − 1 = -1,
invece (-1)3/2 =
(−1) 3 =
− 1 non ha significato nell’ambito dei numeri reali
y
3
f(x) = x 2/3 = x 2 , Df = R , immagine f(Df) = R+
x
Se x ≠ 0 possiamo anche definire x - m/n =
1
m
xn
con m,n ∈ N
Infine si può definire la funzione potenza con esponente reale, definita solo per x > 0
f(x) = x α
Es. f(x) = x 2
con α qualsiasi numero reale, anche irrazionale
Funzione inversa
Se accade che ad ogni y = f(x) ∈ f(Df) corrisponde un unico x ∈ Df allora si dice che la
funzione è invertibile e la funzione che ad ogni y associa l’unico x tale che f(x) =y si chiama
funzione inversa di f e si denota con f –1 ,
f –1 : y =f(x) ∈ f(D f ) → x = f
-1
(f (x) ) = f –1(y) ∈ f(D f ) )
y-2
y-2
=x
invertibile f –1(y) =
3
3
l’operazione di inversione fornisce nuovamente una retta.
Esempi : y = 3x + 2 ⇒ 3x = y –2 ⇒ x =
Invece y =x2 , per esempio 4 = ( ± 2 )2 ⇒ x1 = +2 , x2 = -2 , due valori ⇒ non invertibile
se però considero y = x2 con x ≥ 0 allora si ha solo x1 = +2
4
-2
2
Nota che in questo caso la funzione è monotona (strettamente cresc.) )
e si ha che 4 ≡ (4)1/2 = +2
Quindi la funzione inversa della funzione potenza con n=2 è la funzione radice quadrata :
f –1(y) = y ≡ (y)1/2 =
il dominio di f –1 è R +.
x 2 = x (solo se il dominio di f è ristretto a R +, cioè x ≥ 0). Nota che anche
Quindi: Se f è strettamente monotona (crescente o decrescente) allora è invertibile.
Quindi ad esempio y =f(x) = x 2/3 =
3
f(x) = x è invertibile su tutto R , f
3
x 2 , f –1(f (x) ) → ( x2/3 )3/2 = x , cioè f –1 =
–1
→ 3 ( e viceversa)
Nota 1: il grafico della funzione inversa è simmetrico rispetto alla bisettrice y = x .
( )3
x>0
Se invece di far variare la base facciamo variare l’esponente abbiamo la funzione esponenziale
f(x) = ax , a > 0
Nota:
a x > 0 ∀ x ∈ R.
se
se
a > 1 , a x è strettamente crescente
a < 1 , a x è strettamente decrescente.
Y
a>1
a<1
1
a0 =1
x
Come abbiamo fin qui visto, se una funzione è strettamente monotona allora ∃ la funzione inversa.
La funzione inversa di ax è definita da:
f –1 = log a (logaritmo in base a di ) il cui dominio è R+
(se a = e = numero di Nepero = 2,71828… irrazionale, si ha quindi ex e log x (la base è
sottintesa))
Viceversa : la funzione inversa di log ax è ax .
Quindi per la definizione di funzione inversa si ha :
f-1 f(x) = x ⇒ loga ax = x e a logax = x ,
E quindi per x = 1 risulta ⇒
logaa = 1 e a loga1 = 1 , cioè ⇒ loga1 = 0.
Inoltre si evince che logaxb = b logax
y =f(x) = logax
Nota bene : il dominio di loga x = insieme immagine ax è R+ ( ax sono tutti numeri positivi al variare
di x).
e per x = 0 il logaritmo non è definito.
Dalla proprietà delle potenze ricaviamo le proprietà del logax.
Esempio:
ax1 a x2 = a x1+ x2 ⇒ loga(x1x2) = logax1 + logax2
infatti posto
y1 = logax1 , y2 = logax2
ay1 = x1, ay2 = x2
quindi
ay1 ay2 = ay1+ y2 = x1x2 ⇒ logaa(y1+ y2) = loga(x1 x2)
ma
logaa(y1+ y2) = y1 + y2 = logax1 + logax1.
Cioè il logaritmo del prodotto è uguale alla somma dei logaritmi.
Analogamente si può dimostrare che
loga
x1
= loga x1 - loga x2
x2
Nota sui grafici:
y(x)=f(x)
-f(x) grafico simmetrico rispetto all’asse delle x
f(x-a) traslazione del grafico a destra di a unità di lunghezza
f(x+a) traslazione del grafico a sinistra di a unità di lunghezza
c +f(x) traslazione del grafico in alto di c unità di lunghezza
-c + f(x) traslazione del grafico in basso di c unità di lunghezza
Esercizi
Verificare la Nota sui grafici delle funzioni elementari con a=2 e c=3
Disegnare i grafici delle seguenti funzioni, indicare il loro dominio, indicare gli
intervalli dove sono crescenti e dove decrescenti:
f(x) = 1- 2x2 , f(x) =
1
, f(x) = 1 – log2x (logaritmo naturale, in base e)
1− x
Calcolare la funzione inversa di
disegnare i grafici di f e di f -1.
3
f(x)=3x 4 ,
Calcolare log39, log2 1 , log510 + log5 7
6
indicare il suo dominio e quello della f -1 e