4.5 Valutazione statistica della distribuzione uniforme

Approfondimento 4.5
Valutazione statistica della distribuzione uniforme
delle risposte nei distrattori a un item di prestazione massima
La valutazione statistica della distribuzione uniforme delle risposte nei distrattori ad un item di prestazione massima è una caso particolare del test del chi-quadrato per un campione. Supponiamo di
aver ottenuto una distribuzione di frequenza delle risposte come quelle riportate in Tabella 4.3.1
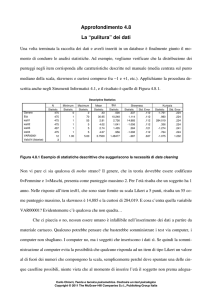
Tabella 4.3.1 Distribuzioni di frequenza delle risposte alle alternative di un item (item1). La cella grigiata indica la frequenza della risposta corretta.
A
B
C
D
Item1
14
55
28
3
Nel caso dell’item in Tabella 4.3.1 osserviamo che 45 soggetti non hanno risposto correttamente
all’item. Questo significa che dovremmo attenderci che, se la distribuzione delle frequenze di risposta nei distrattori fosse uniforme, ogni distrattore dovrebbe avere frequenza uguale a 15, ossia 45
diviso 3. Per verificare statisticamente se questa ipotesi è verosimile, si esegue un test del chiquadrato per un campione. Le ipotesi sono:
H0: la distribuzione delle frequenze nei distrattori è uniforme
H1: la distribuzione delle frequenze nei distrattori non è uniforme
Se possiamo rifiutare l’ipotesi nulla, ci dovrebbe essere almeno un distrattore in cui lo scostamento
fra frequenza osservata e attesa sotto ipotesi di uniformità di distribuzione è statisticamente diverso
da zero. Utilizziamo allora i test post-hoc per il test del chi-quadrato per un campione per approfondire l’analisi. Nella Tabella 4.3.2 sono riportati i calcoli necessari per il caso dell’Item 1
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
2
Tabella 4.3.2 Riepilogo dei test omnibus e post-hoc per la distribuzione di frequenza dei distrattori item 1
2
X calcolato
=
( fo − fa )2
fa
2
Decisione
2
Scostamento non significativo
Scostamento significativo
Scostamento significativo
Scostamento significativo
X (gdl) critico
Test
Alternativa
fo
fa
Post-hoc
A
14
15
0,07
X (1) = 5,02
Post-hoc
C
28
15
11,27
X (1) = 5,02
Post-hoc
D
3
15
9,60
X (1) = 5,02
Omnibus
Somma
45
45
20,93
X (2) = 5,99
2
2
2
Il test omnibus verifica l’ipotesi di uniformità della distribuzione. Il valore del chi-quadrato critico
riportato in Tabella 4.3.2 è quello per α = .05 e gradi di libertà uguale al numero di distrattori meno
uno, ossia 2. Per ottenere questo valore possono essere consultate le tavole di chi-quadrato in un
qualunque manuale di statistica o utilizzare la funzione di Excel =inv.chi(,05;2).
La regola di decisione è:
se X2 calcolato > X2 critico → è troppo improbabile che i dati osservati siano il risultato del fatto
che H0 è vera, per cui la rifiutiamo → la distribuzione non è uniforme
se X2 calcolato ≤ X2 critico → non è così improbabile che i dati osservati siano il risultato del fatto
che H0 è vera, per cui la accettiamo → la distribuzione è uniforme
Dato che il chi-quadrato calcolato (20,93) è maggiore di quello critico (5,99) possiamo rifiutare
l’ipotesi nulla di uniformità della distribuzione. A livello statistico, quindi, le frequenze di risposta
errata non appaiono distribuite uniformemente nei distrattori.
Per verificare in quale o quali distrattori lo scostamento dall’uniformità sia maggiore eseguiamo i test post-hoc. In questo caso il valore del livello di significatività α va diviso per il numero
di gradi di libertà (numero distrattori − 1) per controllare l’inflazione dell’errore di I tipo (si veda a
questo proposito Chiorri, 2010, Approfondimento 4.1). Se abbiamo fissato a α = .05, avremo che
α/2 = ,025. Ogni confronto fra frequenze osservate e attese ha 1 grado di libertà. Il valore di chiquadrato critico per α = ,025 e gdl = 1 [in Excel =inv.chi(,025;1)] è 5,02. La regola di decisione è:
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
3
se X2 calcolato > X2 critico → lo scostamento è significativo
se X2 calcolato ≤ X2 critico → lo scostamento non è significativo
Nel caso della Tabella 4.3.2 abbiamo che lo scostamento non è significativo per l’alternativa di risposta A, mentre lo è per le alternative di risposta C e D. In base ai dati delle frequenze osservate e
attese riportate in Tabella 4.3.2 è facile osservare come l’alternativa C sia stata scelta più di quanto
ci si sarebbe aspettati, mentre l’alternativa D è stata scelta con minore frequenza di quanto atteso.
Poiché la procedura appena presentata è basata su un test del chi-quadrato, è consigliabile calcolare
sempre la dimensione dell’effetto per evitare distorsioni nelle decisioni legate ad ampiezze campionarie troppo ampie o troppo basse. La dimensione dell’effetto w di un test chi-quadrato si ottiene
con la seguente formula (Cohen, 1988):
w=
X2
n
dove X2 è il valore del chi-quadrato calcolato e n il numero di soggetti. La Tabella 4.3.3 riporta le
linee guida per l’interpretazione di w.
Tabella 4.3.3 Interpretazione della dimensione dell’effetto w per il test chi-quadrato
Valore di w
w < 0,10
0,10 < w < 0,30
0,30 < w < 0,50
w > 0,50
Dimensione dell’effetto
Trascurabile
Debole
Moderata
Grande
Nel caso che stiamo considerando, la dimensione dell’effetto generale è w =
20,93
= 0,68 , e dun45
que è una dimensione dell’effetto grande.
In base a questi risultati possiamo concludere che le risposte errate non sembrano ben distribuite nei distrattori. Se invece la distribuzione nei distrattori fosse stata quella di Tabella 4.3.4, la
conclusione sarebbe stata diversa:
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
4
Tabella 4.3.4 Distribuzioni di frequenza delle risposte alle alternative di un item (item 2). La cella grigiata indica la frequenza della risposta corretta.
Item2
8
11
70
11
A
B
C
D
I risultati sono riassunti nella Tabella 4.3.5.
Tabella 4.3.5 Riepilogo dei test omnibus e post-hoc per la distribuzione di frequenza dei distrattori item 2
2
=
X calcolato
( fo − fa )2
fa
2
Decisione
2
Scostamento
gnificativo
Scostamento
gnificativo
Scostamento
gnificativo
Scostamento
gnificativo
Test
Alternativa
fo
fa
X (gdl) critico
Post-hoc
A
8
10
0,40
X (1) = 5,02
Post-hoc
B
11
10
0,10
X (1) = 5,02
Post-hoc
D
11
10
0,10
X (1) = 5,02
Omnibus
Somma
30
30
0,60
X (2) = 5,99
2
2
2
non sinon sinon sinon si-
In questo caso il chi-quadrato calcolato è inferiore a quello critico sia per il test omnibus (0,60 <
5,99), sia per tutte e tre le categorie di distrattori. La dimensione dell’effetto risulta
w=
0,60
= 0,14 , dunque nella gamma debole. Possiamo quindi concludere che le risposte errate
30
sono sostanzialmente equidistribuite nei distrattori.
Eseguire la valutazione statistica della distribuzione uniforme dei distrattori con
Excel
Nel file POLITOMICI.xls troviamo le risposte a 10 item di un test di prestazione massima in cui le
risposte sono codificate con la lettera corrispondente alla risposta data dal soggetto o con BLANK
nel caso di risposta omessa o multipla (Figura 4.3.1)
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
5
Figura 4.3.1 Dataset con item di prestazione massima in cui sono possibili risposte omesse o multiple (BLANK)
Nella prima riga di Figura 4.3.1, nelle celle a sfondo giallo, abbiamo la chiave di risposta, ossia le
risposte corrette. Per quanto la procedura che sta per essere illustrata possa essere realizzata anche
con SPSS (vedi Strumenti Informatici 4.1), con Excel in alcuni casi può essere più rapida.
Nelle celle accanto a quelle contenenti i dati incolliamo, dopo averla copiata (Selezione delle
celle → Tasto Destro del Mouse → Copia), la riga con i nomi degli item (Figura 4.3.2)
Figura 4.3.2 Preparazione del foglio di Excel per lo scoring
Nella cella vuota sotto stp01 sulla destra, scriviamo la formula che permette di fare lo scoring in base al seguente criterio: +1 risposta corretta, -0,25 risposta errata, 0 se BLANK. Utilizziamo la funzione di Excel SE ed espresso in parole il concetto è il seguente:
Se la cella che contiene la risposta del soggetto è uguale alla chiave di risposta, allora 1; altrimenti
se è uguale a BLANK uguale 0, altrimenti -0,25.
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
6
Che nella funzione di Excel diventa:
=SE(A3=A$1;1;SE(A3=”BLANK”;0;-0,25))
dove A3 è la cella che contiene la risposta del primo soggetto, e A1 è la cella che contiene la risposta corretta. L’espressione A$1 indica che la riga 1 va mantenuta fissa, in quanto la procedura di
riempimento per trascinamento farebbe sì che il riferimento alla cella che contiene la risposta corretta venga cambiata per ogni soggetto. L’1 dopo il primo punto e virgola indica che cosa deve essere visualizzato se l’uguaglianza è vera. Ciò che viene dopo il secondo punto e virgola indica invece
cosa succede se la risposta inserita non è corretta: se è uguale a BLANK viene visualizzato 0, altrimenti la risposta è errata, per cui -0,25. Si noti che se la condizione riguarda un numero basta inserire il numero, se è un dato testuale occorre indicarlo fra virgolette. Inoltre occorre prima assicurarsi
che le risposte del dataset siano solo lettere da A ad E e BLANK. Una volta insrita la formula nella
cella L3 e premuto INVIO si ottiene il risultato, che è 1, perché il soggetto ha risposto correttamente
(Figura 4.3.3)
Figura 4.3.3 Risultato della procedura di scoring
Adesso selezioniamo la cella con la formula, spostiamo il puntatore sul quadratino nero in basso a
destra della cella, e quando l’indicatore diventa la crocetta nera, premiamo il Tasto Sinistro del
Mouse. Tenendo premuto il tasto del mouse ci spostiamo verso destra fino a riempire le celle corrispondenti ad ogni item. Rilasciando il tasto del mouse si ottiene l’estensione della formula a tutte le
celle (Figura 4.3.4).
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
7
Figura 4.3.4 Risultato dell’estensione della formula di scoring agli altri item
Conviene sempre controllare che la formula sia stata estesa in modo corretto: in questo caso sì, perché a stp03 c’è un BLANK e il punteggio assegnato è 0, la risposta alla domanda stp04 è errata e
infatti è stato assegnato -0,25, e così via. Ad ogni modo, andando su ogni cella dove è stato generato
lo scoring è possibile controllare la formula corrispondente della riga:
Si presti sempre attenzione a che i riferimenti della chiave di risposta siano quelli corretti.
Selezioniamo ora la prima riga di celle con lo scoring, e con lo stesso procedimento di estensione
delle formule visto prima e riempiamo le righe sottostanti, così da ottenere i punteggi per tutti i soggetti. Si ottiene così lo scoring completo (Figura 4.3.5)
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
8
Figura 4.3.5 Completamento dello scoring
A questo punto è anche facile ottenere il punteggio al test mediante la funzione Somma. Scriviamo
“Punteggio” in una delle colonne accanto all’ultimo item e scriviamo =SOMMA( e una volta scritta
questa espressione (senza premere INVIO), è possibile selezionare direttamente col mouse la riga di
celle che contiene i punteggi del soggetto. Una volta chiusa la parentesi e premuto invio si otterrà il
punteggio totale per il soggetto (Figura 4.3.6)
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
9
Figura 4.3.6 Calcolo del punteggio totale
Di nuovo, con la procedura di estensione della formula verso il basso è possibile rapidamente ottenere il punteggio per tutti i soggetti. Per sicurezza controllate sempre che i conti tornino per tutti i
soggetti.
Potremmo poi essere interessati a determinare, soggetto per soggetto, lo stile risposta, inteso
come numero di risposte corrette, errate o sbagliate. Scriviamo allora “Corrette”, “Errate” ed “Omesse” a destra di “Punteggio” (Figura 4.3.7) e con la funzione CONTA.SE andiamo a calcolare
questi dati:
Figura 4.3.7 Preparazione del foglio di Excel per il calcolo del numero di risposte corrette, errate e
omesse
Sotto a “Corrette” scriviamo:
=CONTA.SE(L3:U3;1)
che vuol dire: “Conta quante celle nell’intervallo che va da L3 a U3 contengono il valore 1”. E poi
Invio. Selezioniamo la cella sotto a Errate e ripetiamo lo stesso procedimento per le risposte errate:
=CONTA.SE(L3:U3;-0,25)
Infine, selezioniamo la cella sotto a Omesse e ripetiamo lo stesso procedimento per le risposte omesse:
=CONTA.SE(L3:U3;0)
A questo punto selezioniamo le tre celle ed estendiamo le formule a tutti i soggetti (Figura 4.3.8)
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
10
Figura 4.3.8 Calcolo del numero di risposte corrette, errate ed omesse per tutti i soggetti
In base a queste informazioni potremmo anche calcolare, indipendentemente dallo scoring iniziale,
il punteggio corretto per guessing (vedi Approfondimento 4.7) mediante la formula:
αC = α −
β
k −1
dove:
•
•
•
•
αC = punteggio corretto per l’effetto di guessing
α = numero grezzo di risposte esatte
β = numero di risposte errate
k = numero di alternative
Nel nostro caso k = 5
Scriviamo allora in una delle celle sulla destra “Guessing” e impostiamo la formula:
=Y3-(Z3/4)
dove Y3 contiene il numero di risposte corrette del primo soggetto, e Z3 il numero di risposte errate
(Figura 4.3.9)
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
11
Figura 4.3.9 Calcolo della correzione per guessing
Il fatto che il punteggio corretto per guessing sia identico al punteggio ottenuto con lo scoring che
abbiamo visto non è casuale. Infatti estendendo la formula a tutti i soggetti i punteggi coincidono
sempre: del resto, forse avevate già intuito che la procedura di scoring che abbiamo adottato è equivalente alla formula della correzione per guessing. Ad ogni modo, abbiamo visto un’altra procedura
che può esserci utile.
Se adesso dovessimo realizzare la classifica dei punteggi, occorrerebbe determinare il rango
di ogni punteggio all’interno di quelli ottenuti. Scriviamo allora “Rango” in una delle celle a destra
(Figura 4.3.10)
Figura 4.3.10 Preparazione del foglio di Excel per il calcolo del rango
Nella cella sotto a “Rango” scriviamo:
=RANGO(AC3;$AC$3:$AC$200;0)
che vuole dire: “determina il rango del punteggio in AC3 all’interno del set di dati compreso da
AC3 a AC200, in ordine discendente (vogliamo che il più bravo abbia rango = 1)”. Se avessimo voluto un ordine ascendente, avremmo dovuto inserire 1 al posto 0 prima dell’ultima parentesi. I simboli del dollaro ($) servono per “bloccare” l’insieme di celle che funge da riferimento per la determinazione del rango (o posizione in classifica). Premendo Invio si ottiene il rango del soggetto, e la
formula può essere estesa a tutti gli altri soggetti come visto in precedenza.
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
12
Passiamo ora a lavorare sugli item. Ci interesserà vedere per ogni item quante volte è stata scelta
una certa alternativa di risposta, ed eventualmente valutare la distribuzione di frequenza nelle alternative errate. Anche questo compito può essere eseguito con SPSS, ma con Excel può essere più
pratico.
Innanzitutto aggiungiamo una colonna alla sinistra della prima nel set di dati. Selezioniamo la prima
colonna, Tasto Destro del Mouse, Inserisci. Poi andiamo in basso fino alla fine del dataset e sempre
nella prima colonna scriviamo le possibili alternative di risposta (Figura 4.3.11)
Figura 4.3.11 Preparazione del foglio di Excel per il calcolo delle frequenze di scelta di ogni alternativa di risposta
Nella cella accanto a quella di A, scriviamo la formula che ci permette di contare quante volte la risposta A è stata fornita nella colonna che contiene le risposte all’item stp01
=CONTA.SE(B$3:B$200;$A202)
dove A202 è la cella che contiene il valore “A”. Così facendo, quando scorreremo verso il basso le
celle, Excel considererà ogni volta una nuova alternativa di risposta (B, C, D, etc.). Inoltre, blocchiamo le celle da 3 a 200 perché poi ci servirà di estendere le formule verso il basso e la colonna A
perché ci servirà ad estendere le celle verso destra. Dopo aver premuto Invio avremo il risultato. Estendendo le formule verso destra calcoliamo quante volte è stato risposto A per ognuno degli item.
Estendendo adesso questa selezione verso il basso otteniamo il riempimento del resto dei dati. Conviene riportare sopra ad ogni colonna il nome dell’item (Figura 4.3.12).
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
13
Figura 4.3.12 Calcolo del numero di volte che ogni alternativa di risposta è stata scelta per ogni item
Adesso sappiamo per ogni item quante volte è comparsa ogni alternativa di risposta. A questo punto, ci serve di sapere, al netto delle BLANK, come si sono distribuite le risposte errate. Un risultato
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
14
che deporrebbe a favore dell’adeguatezza dell’item e in particolare delle sue alternative di risposta
sarebbe quello per cui le risposte errate sono distribuite uniformemente nelle alternative sbagliate (o
distrattori). Intanto calcoliamo tramite Excel la percentuale di risposte corrette, errate ed omesse
(BLANK). Copiamo la riga delle risposte corrette in una riga a “portata di mano” e scriviamo le etichette delle righe (Figura 4.3.13)
Figura 4.3.13 Preparazione del foglio di Excel per il calcolo del numero di risposte giuste, sbagliate
ed omesse per ogni item
Nella cella corrispondente a Giuste della colonna di stp01 chiederemo di contare tutte le celle
dell’intera colonna che contengono la lettera E, mentre nella cella corrispondente a Omesse chiederemo di riportare il già calcolato numero di celle che contengono l’esito BLANK. La frequenza nella cella corrispondente a Sbagliate sarà uguale alla differenza fra il totale dei soggetti e la somma
fra Giuste e Omesse (Figura 4.3.14).
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
15
Figura 4.3.14 Calcolo del numero di risposte giuste, sbagliate ed omesse per il primo item
A questo punto estendiamo le formule a tutte le celle verso destra e otteniamo i valori desiderati per
ogni item (Figura 4.3.15).
Figura 4.3.15 Calcolo del numero di risposte giuste, sbagliate ed omesse per ogni item
Per trasformare i dati di frequenza in proporzioni, dobbiamo dividere le frequenze per il totale dei
soggetti (in questo caso 198). Estendiamo poi le formule prima verso destra e poi verso il basso,
completando la tabella (Figura 4.3.16).
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
16
Figura 4.3.15 Calcolo della percentuale di risposte giuste, sbagliate ed omesse per ogni item
Volendo, le celle in esame possono essere formattate come percentuali.
La procedura in Excel per eseguire il test del chi-quadrato per l’uniformità della distribuzione di frequenza nei distrattori potrà ora apparire un po’ elaborata, per così dire, ma con un po’ di
pazienza si raggiunge lo scopo.
Per prima cosa otteniamo, item per item, la distribuzione di frequenza delle risposte sbagliate. Scriviamo le cinque alternative di risposta sulla colonna all’estrema sinistra (Figura 4.3.16)
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
17
Figura 4.3.16 Preparazione del foglio di Excel per l’analisi dell’uniformità dei distrattori
A questo punto chiediamo ad Excel di eseguire quanto segue: se la cella con l’alternativa di risposta
in esame è quella della risposta corretta, non visualizzare niente (“”), altrimenti restituisci la frequenza osservata:
=SE($A221=B$210;””;B203)
In questo modo avremo un valore solo se l’alternativa di risposta è quella sbagliata. Estendiamo poi
la formula verso il basso e verso destra, in modo da ottenere la distribuzione di frequenza delle alternative errate per tutti gli item (Figura 4.3.17).
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
18
Figura 4.3.17 Generazione della distribuzione di frequenza dei distrattori
Adesso abbiamo bisogno di calcolare le frequenze attese, il che significa la somma delle frequenze
delle risposte errate diviso per il numero di alternative errate, che è quattro. Prepariamo una nuova
tabella sotto alle frequenze osservate (Figura 4.3.18).
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
19
Figura 4.3.18 Preparazione del foglio di Excel per il calcolo delle frequenze attese nei distrattori
La formula è: se la cella è vuota, non restituire niente; altrimenti, il restituire il totale delle errate diviso per quattro:
=SE(B221=””;””;B$212/4)
Estendiamo poi le formule verso il basso e a destra (Figura 4.3.19)
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
20
Figura 4.3.19 Calcolo delle frequenze attese nei distrattori
Calcoliamo ora i termini del chi-quadrato, sempre in base al ragionamento: se la cella è vuota, la( fO − f A ) 2
:
sciare vuota; altrimenti calcolare
fA
=SE(B221=””;””;(B221-B228)^2/B228)
Di nuovo estendiamo le formule per righe e per colonne (Figura 4.3.20)
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
21
Figura 4.3.20 Calcolo delle componenti del chi-quadrato
Non ci resta ora che calcolare il chi-quadrato, associargli i gradi di libertà (gdlche sono sempre 3) e
quindi la probabilità p che i dati osservati siano il risultato di un’ipotesi nulla vera. Il foglio di Excel
deve essere preparato come in Figura 4.3.21
Figura 4.3.21 Preparazione del foglio di Excel per il calcolo del chi-quadrato
Per ottenere il chi-quadrato occorre sommare le cinque celle corrispondenti alle alternative di risposta (quella vuota tanto non viene considerata). Il valore dei gradi di libertà è sempre 3, per cui basta
inserirlo. Per il valore di p utilizziamo la funzione di Excel DISTRIB.CHI. Dobbiamo scrivere:
=DISTRIB.CHI e poi, nella parentesi, vanno indicati valore di chi-quadrato e gradi di libertà, separati dal punto e virgola:
=DISTRIB.CHI(B241;3)
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
22
Per calcolare il coefficiente di contingenza C, utilizziamo la formula C =
è possibile calcolare la dimensione dell’effetto w con la formula w =
X2
. A partire da C
X2 +n
C2
. Infine, e chiediamo
1− C2
che venga scritta l’interpretazione della dimensione dell’effetto in base ai vincoli: se w inferiore a
,10, allora scrivere “Trascurabile”; altrimenti, se inferiore a ,30, allora scrivere “Piccolo”; altrimenti, se inferiore a ,50, allora scrivere “Moderato”; altrimenti, scrivere “Grande”. Attenzione alle parentesi. Estendiamo infine le formule verso destra e otteniamo i valori desiderati per tutti gli item.
Tutto questo procedimento è illustrato in Figura 4.3.22.
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
23
Figura 4.3.22 Preparazione del foglio di Excel per il calcolo del chi-quadrato
Si può osservare come il valore di p sia particolarmente basso in buona parte degli item (attenzione
a ,000: non è “uguale a zero” ma “inferiore a ,001”, per cui andrà riportato < ,001), tranne che in
stp07, stp09 e stp10, dove p > ,05. In tutti questi casi, in effetti, la dimensione dell’effetto risulta
“Piccola” o “Moderata”. Se in questi item, quindi, è rispettata l’assunzione dell’uniformità della distribuzione delle frequenze di risposta alle alternative errate, nelle altre no. I test post-hoc ci diranno
quale alternativa è stata scelta con maggiore frequenza rispetto alle altre. Abbiamo visto prima come per ogni alternativa di risposta vada calcolato un valore di chi-quadrato critico che ha 1 grado di
libertà e un valore di probabilità uguale a ,05 diviso il numero di alternative errate meno 1. Nel nostro caso abbiamo 4 alternative di risposta errate, per cui dobbiamo dividere ,05 per 3. Otteniamo
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
24
quindi ,0167. A questo punto utilizziamo una formula di Excel per ottenere il valore di chi-quadrato
critico per ogni alternativa, che sarà:
=INV.CHI(,0167;1)
Il risultato è 5,73. Adesso, prepariamo il file con le alternative di risposta e nella cella accanto alla
prima alternativa scriviamo:
=SE(B234=””;””;se(B234<5,73;””;”Rifiuta H0”))
dove B234 contiene il valore calcolato della componente di chi-quadrato. A quel punto estendiamo
la selezione verso il basso e verso destra (Figura 4.3.23)
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia
Approfondimento 4.5 – Valutazione statistica della distribuzione uniforme delle risposte
25
Figura 4.3.23 Esecuzione dei post-hoc per il test del chi-quadrato
Adesso siamo in grado di stabilire per quali item e per quali alternative di risposta non vi è uniformità di distribuzione delle frequenze nei distrattori.
Carlo Chiorri, Teoria e tecnica psicometrica. Costruire un test psicologico
Copyright © 2011 The McGraw-Hill Companies S.r.l., Publishing Group Italia