Efficienza secondo i criteri di first
best
Ruolo del settore pubblico
Intervento dello Stato
• L’economia pubblica giustifica l’intervento
dello Stato nell’economia in presenza di
fallimenti del mercato
• Fallimenti rispetto a quale obiettivo?
• L’obiettivo della allocazione efficiente delle
risorse (scarse) disponibili in un dato
momento in una collettività
1
Economia del benessere
Quali sono le caratteristiche di un sistema economico
in grado di garantire il massimo benessere collettivo?
• Cosa produrre
• Come produrre
• A chi destinare la produzione
Efficienza economica
• Efficienza nello scambio
• Efficienza nella produzione
• Efficienza nella composizione del prodotto
2
Criterio di scelta
• Efficienza paretiana (Vilfredo Pareto)
Una allocazione delle risorse costituisce un
ottimo paretiano quando non è possibile
modificare l’allocazione tra gli individui in
modo tale da migliorare la situazione di
qualcuno senza nel contempo peggiorare
quella di un altro
Efficienza allocativa
• Iniziamo col dimostrare le condizioni che
garantiscono una allocazione efficiente delle risorse
• Dimostriamo che un’economia in cui le risorse
vengono allocate in mercati perfettamente
concorrenziali garantisce l’ottimo di First best (primo
rango)
• Prescindiamo per il momento da questioni
distributive
3
Economia 2 X 2 X 2
• Esistono due individui che agiscono come
consumatori, due imprese che agiscono come
offerenti e che producono due diverse merci
(una ciascuna) impiegando entrambe due
fattori di produzione. Supponiamo quindi che
esistano solo due individui, A e B (Paolo e
Maria), due soli input produttivi K e L, e due
sole merci X e Y, prodotte rispettivamente da
due imprese.
Efficienza nello scambio
Due individui
4
Allocazione delle risorse
• Consideriamo un’economia senza produzione (o
con auto-produzione)
• Supponiamo che i due individui dispongano di
una quantità data di bene X e di bene Y, ovvero X , Y
• Allocazione significa che i due individui devono
trovare un modo di dividere tra loro le quantità
disponibili dei due beni.
• Esiste una allocazione iniziale dei beni: gli
individui scambiano tra loro in modo da
raggiungere una allocazione che sia preferita da
almeno uno dei due.
Allocazione
• Supponiamo che:
X = 10 (ad esempio pesci)
Y = 20 (ad esempio noci di cocco)
• Allocare significa suddividere queste quantità
date di beni tra i due individui
• Ricordiamo che gli individui traggono utilità dal
consumo dei beni
5
Consumatore Paolo
Quantità di bene Y
0
Quantità di bene X
Consumatore Maria
Quantità di bene Y
0
Quantità di bene X
6
Scatola di Edgeworth-Bowley
• Riunisce i due grafici relativi ai due
consumatori in uno spazio chiuso e limitato
dalla disponibilità dei due beni
• All’interno della scatola sono rappresentabili
tutte le allocazioni possibili di X ed Y tra i due
consumatori
Y
Allocazione di Paolo
YP
0
.
V
XP
X
V è l’allocazione iniziale
7
Y
Allocazione di Paolo
Maria
.
YP
0
V
XP
Maria
V è l’allocazione iniziale
XM
YP
V
0
Paolo
V è l’allocazione iniziale
X
.
Maria
0
YM
XP
8
0
Quantità di bene Y
U1
U2
U3
U1
0
U2
U3
Quantità di bene X
Maria
0
YM
V
YP
.
0
Paolo
XP
XM
9
• V è l’allocazione iniziale in cui:
– Paolo possiede ( X P , YP )
– Maria possiede ( X M , YM )
• Dimostriamo che attraverso lo scambio, i due
individui riescono a migliorare la loro
posizione (utilità)
Maria
U2
U1
0
U3
Z
V
0
.
Paolo
10
Maria
U2
U1
0
U3
Z
V
.
0
Paolo cede bene X in cambio di bene Y
Z rappresenta un miglioramento paretiano
rispetto a V
• Nell’allocazione Z Paolo passa dalla curva di
indifferenza 1 alla 3, quindi aumenta il suo
benessere
• Nell’allocazione Z Maria è indifferente rispetto
a V perché resta sulla stessa curva di
indifferenza.
• Paolo migliora mentre Maria non peggiora: Z è
preferito complessivamente a V
11
Z è un punto di equilibrio
• Nel punto Z le due curve di indifferenza
sono tangenti:
– Il SMS tra X ed Y di Maria è uguale al SMS tra X
ed Y di Paolo
• Condizione di efficienza n. 2
– Quindi:
SMS Paolo X ,Y =
SMS
Maria
X ,Y
UMg P X
=
UMg PY
UMg M X
=
UMg MY
Maria
U1P
U 2P
0
U 3P
K
.
0
V
M
U 2M U1
Paolo
12
K è preferito a V
• Spostandosi nella allocazione K entrambi gli
individui migliorano il loro benessere
• K è strettamente preferito rispetto a V
• Anche in K si ha uguaglianza nei saggi
marginali di sostituzione tra X ed Y dei due
consumatori
Maria
U1P
U 2P
U 3P
.
H
U 3M
0
0
V
M
U 2M U1
Paolo
13
H è preferito a V
• Nella allocazione H Maria ha un maggiore
benessere rispetto a V
• Paolo è indifferente tra H e V
• La collettività nel suo complesso guadagna
spostandosi da V a H
Maria
0
Y
U1M
U 2M
Z
U 3M
U 3P
K
H
U 2P
U1P
Curva dei contratti
0
Paolo
X
14
La curva dei contratti
• È il luogo dei punti che costituiscono allocazioni
Pareto-efficienti
• In ciascuno di questi punti, non è più possibile
migliorare il benessere di un individuo se non
peggiorando la situazione dell’altro individuo
• Il criterio di Pareto non ci dice quale tra i punti
che costituiscono la curva dei contratti sia il
migliore per la collettività
• Ogni punto sulla linea dei contratti è associato a
due diversi livelli di utilità, uno per ciascun
individuo.
Maria ha un ordinamento H > K > Z
Y
Maria
0
U1M
U 2M
Z
U 3M
U 3P
K
H
U 2P
U1P
Curva dei contratti
0
Paolo
X
Paolo ha un ordinamento Z > K > H
15
Curva delle possibilità di utilità
• In ogni suo punto ci dice quale è la massima
utilità di cui può godere Paolo, dato un certo
livello di utilità assegnato a Maria
• È una curva decrescente (se aumento l’utilità
di Paolo, devo ridurre quella di Maria)
U 1P → U 3M
U 2P → U 2M
U 3P → U 1M
Curva delle possibilità di utilità
Utilità di
Maria
UM3
H
K
UM2
Z
UM1
0
UP1
UP2
UP3
Utilità di Paolo
16
Efficienza nella produzione
Due imprese, X e Y
Due fattori K e L
Efficienza nella produzione
• L’economia deve produrre la massima
quantità possibile di beni, sfruttando al
meglio i fattori della produzione disponibili
• Le quantità disponibili di K e di L sono date
e le imprese si spartiscono tali quantità per
produrre il proprio bene in maniera
efficiente
K = K X + KY
L = LX + LY
17
Efficienza nella produzione
• La produzione senza sprechi è
rappresentabile mediante la frontiera della
produzione
• Se l’impresa X produce una grande quantità
di bene, l’impresa Y avrà a disposizione
meno fattori e potrà produrre una quantità
minore del suo bene.
• L’allocazione dei fattori tra le due imprese
determina le quantità di prodotto
disponibili
0
Impresa Y
K
Q1Y
Q2Y
Q3Y
Q3X
K1X
Q2X
Q1X
0
LX
1
L
Impresa X
18
Condizione di efficienza n.1
• Poiché i punti di equilibrio sono punti di
tangenza tra gli isoquanti dell’impresa X e
dell’impresa Y, allora
STSKX,L = STSY
K ,L
∆K
PMGL
STS =
=
∆L
PMGK
PMGLX
PMGY
L
=
PMGKX
PMGY
K
0
Impresa Y
K
Q1Y
Q2Y
Q3Y
Q3X
K 2X
Q2X
Q1X
0
LX2
L
Impresa X
19
Quantità di bene Y
La frontiera della
produzione indica la
massima quantità
producibile di un bene,
data la quantità prodotta
di un altro bene
QY3
Q1Y
0
Q1X
Q3X
Quantità di bene X
Frontiera della produzione
Quantità di bene Y
QY3
P
Q1Y
0
Q1X
Q3X
Quantità di bene X
Frontiera della produzione
20
Inefficienza
Quantità di bene Y
Z è inefficiente
perché è possibile aumentare
la produzione sfruttando al
meglio i fattori
Z
0
Quantità di bene X
Saggio marginale di trasformazione: SMTXY
Y
∆Y
P
0
∆X
P’
X
21
Saggio marginale di trasformazione
∆Y
∆X
Di quanto occorre
ridurre la
produzione di Y
per avere un
aumento della
produzione di X in
assenza di sprechi
Efficienza nella composizione del prodotto
• Le imprese nell’intento di massimizzare il
profitto producono quei beni che
maggiormente soddisfano le preferenze dei
consumatori
• Supponiamo inizialmente che tutti i
consumatori abbiano i medesimi gusti e
quindi le stesse curve di indifferenza
22
Supponiamo che tutti i consumatori
abbiano le medesime preferenze
Y
E = equilibrio
Curva di indiff.
Curva delle poss.
di prod.
X
Supponiamo che tutti i consumatori
abbiano le medesime preferenze
Y
YE
XE
X
23
Combinazione efficiente (consumatori diversi)
Y
P
YE
Frontiera
produzione
UM1
UMX 2
E
UP2
UP1
0
X
Combinazione efficiente
SMTXY = SMSXY (Paolo) = SMSXY (Maria)
Y
P
w
0
Le due linee rosse hanno la stessa
pendenza in equilibrio
X
24
Condizioni di efficienza n.3
L’allocazione delle risorse è efficiente quando i
saggi marginali di sostituzione uguagliano il
tasso marginale di trasformazione
Poiché i consumatori uguagliano SMS ai
rapporto tra i prezzi:
SMS XP ,,YM =
px
= SMTX ,Y
py
Efficienza paretiana e sistema di
mercato concorrenziale
Primo Teorema:
“Ogni allocazione delle risorse generata come
equilibrio generale di un sistema
concorrenziale costituisce un ottimo paretiano”
25
Combinazione efficiente
SMTXY = SMSXY (Paolo) = SMSXY (Maria)
Y
P
Y
px
py
w
px
py
0
X
X
Altre condizioni che si realizzano
• Per le imprese, posto che i mercati dei fattori
sono concorrenziali
TMS X L,K = TMSY
L,K =
• Le imprese massimizzano il profitto:
w
r
PX = MC X
PY = MCY
26
In conclusione
SMS X ,Y =
PX
MC X
=
= SMTX ,Y
PY
MCY
Efficienza paretiana e sistema di
mercato concorrenziale
Secondo Teorema:
“Ogni allocazione delle risorse che costituisce
un ottimo paretiano può essere generata
mediante un equilibrio generale di un sistema
concorrenziale data una correzione iniziale
delle allocazioni effettuata con imposte e
trasferimenti non-distorsivi”
27
Maria
0
Y
B
A
V
0
Paolo
X
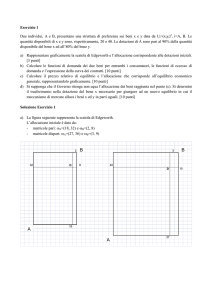
Secondo teorema
• Supponiamo che V sia l’allocazione di partenza
• Da essa, mediante il libero scambio, si può
raggiungere l’equilibrio paretiano A.
• Supponiamo che lo Stato desideri invece raggiungere
l’allocazione B (da V è impossibile)
• Lo stato può modificare l’allocazione INIZIALE da V a
V’ e lasciare poi che il libero scambio porti gli
individui nel punto B
28
Maria
0
Y
B
V’
A
V
0
X
Paolo
Da V a V’
• Nello spostamento da V a V’ Paolo riceve un
trasferimento mentre Maria paga un’imposta
in somma fissa
29