9788863641806_ I-II _romane:9788863640366_Colophon
18-01-2010
16:54
Pagina 1
WALKER
CORSO DI
FISICA
LABORATORIO
a cura di
CLAUDIO MASSA e TIZIANA VANDELLI
9788863641806_ I-II _romane:9788863640366_Colophon
18-01-2010
16:54
Tutti i diritti riservati
© 2010, Pearson Italia spa, Milano-Torino
www.pearson.it
A cura di
Claudio Massa e Tiziana Vandelli
Responsabile editoriale
Valeria Cappa
Progettazione grafica,
impaginazione e realizzazione
dei disegni
ConEdit Libri srl, Cormano (Mi)
Coordinamento tecnico grafico
e controllo qualità
Michele Pomponio
Copertina
Italik, Milano
Immagine di copertina
© Larry Kasperek/NewSport/Corbis
Le immagini sono dell’Archivio iconografico Pearson Italia.
Per i passi antologici, per le citazioni, per le riproduzioni grafiche, cartografiche e fotografiche appartenenti alla proprietà di terzi, inseriti in quest’opera, l’editore è a disposizione degli aventi diritto non potuti reperire nonché per eventuali non volute
omissioni e/o errori di attribuzione nei riferimenti. È vietata la riproduzione, anche
parziale o a uso interno didattico, con qualsiasi mezzo, non autorizzata.
Le fotocopie per uso personale del lettore possono essere effettuate nei limiti del 15%
di ciascun volume dietro pagamento alla SIAE del compenso previsto dall’art. 68,
commi 4 e 5, della legge 22 aprile 1941 n. 633. Le riproduzioni effettuate per finalità di
carattere professionale, economico o commerciale o comunque per uso diverso da
quello personale possono essere effettuate a seguito di specifica autorizzazione rilasciata da:
AIDRO
Corso di Porta Romana n. 108
20122 Milano
e-mail [email protected]
sito web www.aidro.org
Stampato per conto della casa editrice presso:
La Fotocromo Emiliana, Osteria Grande (Bo), Italia
Ristampa
0 1 2 3 4 5
Anno
10 11 12 13 14 15
9788863641806
www.linxedizioni.it
Pagina II
9788863641806_ I-II _romane:9788863640366_Colophon 15/01/10 10:31 Pagina III
Indice dei laboratori
1. Determinazione dello spessore di un foglio
di carta utilizzando il calibro ......................................
2. Confronto fra la misura diretta e la misura
indiretta di un’area ........................................................
3. Confronto fra la misura diretta e la misura
indiretta di un volume .................................................
4. Misura della velocità media e della velocità
istantanea di un oggetto .............................................
5. Moto accelerato ...............................................................
6. Verifica della regola del parallelogramma .........
7. Moto parabolico ..............................................................
8. Taratura di un dinamometro ....................................
9. Verifica della seconda legge di Newton ..............
10. Scomposizione della forza peso in un piano
inclinato ...............................................................................
11. Stima dell’attrito dinamico ........................................
12. Determinazione del coefficiente di attrito
statico tra due superfici ...............................................
13. Legge di Hooke ...............................................................
14. Verifica del teorema delle “forze vive” .................
15. Trasformazione dell’energia potenziale
di una molla in energia cinetica ..............................
16. Urto anelastico in una dimensione ........................
17. Pendolo balistico .............................................................
18. Urto elastico in una dimensione .............................
19. Moto circolare uniforme e accelerazione
centripeta ............................................................................
20. Confronto fra oggetti che rotolano
(senza strisciare) su un piano inclinato ...............
21. Determinazione del centro di massa
di un oggetto .....................................................................
22. Accelerazione angolare ................................................
23. Determinazione del momento d’inerzia .............
24. Sistema massa-molla .....................................................
25. Relazione fra lunghezza e periodo
di un pendolo semplice ...............................................
26. Misura di g con il pendolo .........................................
27. Misure di densità ............................................................
28. Spinta di Archimede .....................................................
2
3
4
6
8
10
11
12
13
15
16
18
19
20
22
23
24
25
27
28
29
30
31
32
33
35
36
37
29. Verifica della legge di Torricelli ...............................
30. Dilatazione termica ........................................................
31. Calore specifico ................................................................
32. Trasformazioni a temperatura costante ...............
33. Trasformazioni a pressione costante .....................
34. Trasformazioni a volume costante .........................
35. Calore latente di fusione .............................................
36. Taratura di un termometro ........................................
37. Interferenza delle onde sonore ................................
38. Onde stazionarie .............................................................
39. Riflessione della luce ....................................................
40. Specchio sferico ...............................................................
41. Rifrazione ...........................................................................
42. Lente convergente ..........................................................
43. Microscopio composto .................................................
44. Telescopio di Galileo .....................................................
45. Interferenza della luce ..................................................
46. Diffrazione .........................................................................
47. Legge di Coulomb ..........................................................
48. Verifica della legge di Ohm .......................................
49. Curva tensione-corrente
di una lampadina ............................................................
50. Resistività dei materiali ...............................................
51. Resistenze in serie e in parallelo .............................
52. Misura della costante di tempo
nei circuiti RC ...................................................................
53. Resistenza interna di una pila ..................................
54. Misura della carica specifica dell’elettrone ..........
55. Forza magnetica esercitata su un filo
percorso da corrente ......................................................
56. Campo magnetico prodotto da una corrente
rettilinea ...............................................................................
57. Equazione del trasformatore ....................................
58. Impedenza di un circuito in corrente
alternata ...............................................................................
59. Angolo di Brewster ........................................................
60. Determinazione della costante di Planck
mediante l’effetto fotoelettrico .................................
61. Spettro dell’atomo di idrogeno ................................
38
39
40
42
43
45
47
48
49
50
51
52
53
55
56
57
58
59
60
61
62
63
65
66
67
68
70
72
73
74
75
76
77
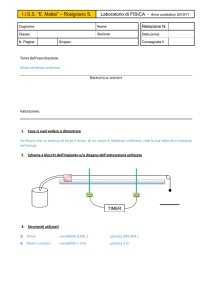
LABORATORIO
1
Determinazione dello spessore di un
foglio di carta utilizzando il calibro
Obiettivo
Svolgimento
Misurare lo spessore di un foglio di
carta in formato A4 utilizzando un
calibro centesimale.
La misura dello spessore di un foglio di carta non può essere affrontata direttamente, essendo il foglio di carta estremamente sottile. Possiamo superare questa
difficoltà ricorrendo a una pratica sperimentale nota come metodo della chiusura.
Supponendo che i fogli abbiano tutti il medesimo spessore, misuriamo lo spessore
di n fogli e dividiamo poi il risultato della misura per il numero n. In questo modo
anche l’incertezza sulla misura sarà ottenuta dividendo per n il valore relativo alla
misura complessiva.
Procediamo, quindi, misurando lo spessore di 20 fogli sovrapposti uno sull’altro.
Prepariamo 5 pacchetti da 20 fogli ciascuno ed eseguiamo la misura.
Riportiamo i dati nella seguente tabella:
Materiale occorrente
o Una risma di fogli di carta in
formato A4
o Un calibro centesimale
TABELLA 1
Pacchetto
1
2
3
4
5
Spessore (mm)
Spessore medio di un pacchetto: xmedio( 20 ) ...................... mm
Spessore massimo di un pacchetto: xmax( 20 ) ...................... mm
Spessore minimo di un pacchetto: xmin( 20 ) ...................... mm
Semidispersione massima a ¢x xmax xmin
b: ¢x( 20 ) ...................... mm
2
Calcoliamo lo spessore di un foglio dividendo per 20 lo spessore medio e la semidispersione di un pacchetto:
xmedio .................... mm
¢x .................... mm
Confrontiamo ora la semidispersione massima con la sensibilità dello strumento: il
maggiore di questi due valori corrisponde all’incertezza associata alla misura.
Ricordiamo che l’incertezza non può essere mai inferiore alla sensibilità dello strumento utilizzato.
Risultato
Arrotondiamo il valore dell’incertezza alla prima cifra significativa e confrontiamola con il valore medio della misura effettuata, verificando su quale cifra incide
l’incertezza. Arrotondiamo il risultato alla prima cifra certa.
Scriviamo il risultato:
x (...................... ; ......................) mm
Osservazioni
Sottolineiamo che il ricorso al metodo della chiusura presuppone che tutti i fogli abbiano lo stesso spessore.
Quesiti
• Esponi sotto forma di relazione i procedimenti seguiti, mettendo in evidenza l’obiettivo, il materiale e gli strumenti utilizzati e le scelte operative, motivandole adeguatamente.
2
LABORATORIO
2
Confronto fra la misura diretta
e la misura indiretta di un’area
Obiettivo
Misurare l’area di una superficie piana
con il metodo diretto (per confronto
con un campione di superficie) e con il
metodo indiretto (mediante relazioni
matematiche a partire dalla misura delle singole dimensioni).
Materiale occorrente
o Un righello millimetrato
o Carta millimetrata
o Figure piane di forma irregolare,
ma scomponibili in triangoli
e rettangoli.
Svolgimento
Misura diretta
Per effettuare la misura diretta dell’area di una figura piana, appoggia la figura sul
foglio di carta millimetrata e ricalcane il contorno sul foglio.
Ora, prendendo come unità di misura un quadratino da 1 mm2, conta quanti quadratini sono contenuti esattamente all’interno del contorno (non conteggiare quelli attraversati dal contorno) e riporta nella tabella 1 il valore trovato. Questa misura rappresenta un’approssimazione per difetto dell’area.
Conta ora i quadretti che sono attraversati dal contorno e sommali a quelli interni
contati prima. Otterrai così un’approssimazione della misura dell’area per eccesso.
Riporta anche questa misura nella colonna corrispondente della tabella 1.
La misura dell’area è, chiaramente, intermedia ai valori trovati, la migliore stima
del risultato di questa misura è la media aritmetica tra le due misure trovate. Calcola quindi il valore medio e inseriscilo nella colonna corrispondente della tabella.
Ripeti l’intero procedimento per altre 4 volte, ridisegnando il contorno della figura in una posizione diversa del foglio (o di un altro foglio, se necessario).
Calcola ora la media A fra i valori medi che hai trovato e la loro semidispersione, ¢A:
A ...................... mm 2
¢ A ...................... mm 2
Arrotonda l’incertezza alla prima cifra significativa e confronta il valore ottenuto
con la misura dell’area, determinando la cifra sulla quale incide l’incertezza. Arrotonda la misura dell’area alla cifra sulla quale incide l’incertezza e scrivi il risultato ottenuto:
A (...................... ; ......................) mm 2
Misura indiretta
Scomponi la figura in triangoli e in rettangoli aiutandoti con una matita. Per ogni
figura della scomposizione misura la base e l’altezza, riportando in tabella le misure rilevate. Calcola l’area e associa a ogni misura l’incertezza, ricordando la tecnica per il calcolo dell’incertezza nei prodotti.
Calcola, infine, l’area totale e l’incertezza a essa associata.
TABELLA 2
Figura
TABELLA 1
n
Misura per
difetto
1
Base
Altezza
Area
Incertezza
1
Misura per
eccesso
Valore
medio
2
...
...
2
Area totale
3
Arrotonda l’incertezza alla prima cifra significativa e osserva su quale cifra del risultato incide l’incertezza. Arrotonda il risultato alla cifra sulla quale incide l’incertezza e presenta il risultato:
4
5
A (...................... ; ......................) mm 2
Quesiti
• Confronta i risultati ottenuti utilizzando i due diversi procedimenti. Quale delle due misure è più precisa? In quale modo puoi stabilirlo?
• La misura indiretta è sempre possibile?
3
LABORATORIO
3
Confronto fra la misura diretta
e la misura indiretta di un volume
Obiettivo
Misurare il volume di un solido di forma
regolare, un parallelepipedo rettangolo
o una sfera, con il metodo diretto (per
immersione) e con il metodo indiretto
(mediante relazioni matematiche a partire dalla misura delle singole dimensioni).
Svolgimento
Misura diretta
Riempi d’acqua il cilindro graduato fino a un livello che ti consenta poi di immergervi completamente il parallelepipedo e annota nella tabella 1 il volume iniziale
Vi del liquido.
Materiale occorrente
o Un calibro centesimale
o Un cilindro graduato
o Solidi di forma regolare che non si
sciolgono in acqua
(un parallelepipedo rettangolo
e una sfera)
Immergi quindi il solido e annota in tabella 1 il volume finale Vf raggiunto dall’acqua dopo l’immersione del solido.
Il volume del solido si ottiene dalla differenza fra Vf e Vi. L’incertezza su questa
misura è la somma delle incertezze sulle singole misure.
TABELLA 1
Vi (cm3)
¢Vi (cm3)
Vf (cm3)
¢Vf (cm3)
Risultato
V (...................... ; ......................) cm 3
Misura indiretta
Riporta in tabella 2 la misura delle dimensioni del parallelepipedo, effettuata con il
calibro centesimale: base b, altezza h e profondità p. Come incertezza puoi associare a ogni misura la sensibilità dello strumento.
TABELLA 2
b (cm)
¢b (cm)
h (cm)
¢h (cm)
p (cm)
¢p (cm)
Il volume del solido è:
V b p h ......................
Per calcolare l’incertezza sul volume si calcola dapprima l’incertezza relativa, come somma delle singole incertezze relative:
¢V
¢b ¢ p ¢h
......................
V
b
p
h
Quindi:
¢V ...................... V .......................
Risultato
V (...................... ; ......................) cm 3
4
Svolgimento
Misura diretta
Prendiamo in considerazione la sfera.
Procedi esattamente come per il parallelepipedo, compilando la tabella 3.
TABELLA 3
Vi (cm3)
¢Vi (cm3)
Vf (cm3)
¢Vf (cm3)
Risultato
V (...................... ; ......................) cm 3
Misura indiretta
Misura, con il calibro centesimale, il diametro d della sfera associando un’incertezza pari alla sensibilità dello strumento:
d (...................... ; ......................) cm
Il volume è:
V ......................
L’incertezza sul volume, considerato che questo si ottiene da un prodotto, è data
da:
¢V
......................
V
da cui:
V ......................
Risultato
V (...................... ; ......................) cm 3
Osservazioni
Nella misura diretta, è critica la misura del livello dell’acqua nel cilindro graduato. Fai molta attenzione al possibile
errore di parallasse e all’effetto determinato dall’aderenza dell’acqua alla superficie di vetro del cilindro.
Quesiti
• Quale delle due misure è risultata più precisa? Sai spiegarne il motivo?
5
LABORATORIO
4
Misura della velocità media e
della velocità istantanea di un oggetto
Obiettivo
Svolgimento
Effettuare la misura della velocità (media e istantanea) di un carrello che si
muove su una rotaia a cuscino d’aria.
Dopo aver montato l’apparato illustrato in figura ed esserti assicurato, mediante la livella a bolla, che la rotaia sia perfettamente orizzontale, costruisci una tabella analoga alla tabella 1, riportando nella seconda colonna la posizione delle
fotocellule, misurata ponendo l’origine sulla prima fotocellula (F1).
Nella terza colonna riporta gli spostamenti ¢ s1 x2 x1 , ¢ s2 x3 x2 ,...
Materiale occorrente
o Una rotaia a cuscino d’aria
o Un carrello
o Almeno 4 fotocellule
o Un cronometro digitale collegato
alle fotocellule (sensibile
al centesimo di secondo)
o Un metro (sensibile al mm)
o Una livella a bolla
o Un compressore
o Fogli di carta millimetrata
Ricorda che, se la sensibilità del metro è di 1 mm, l’incertezza sulla posizione è
2 mm (1 mm di incertezza sul primo estremo del metro e 1 mm sul secondo estremo) e quella sullo spostamento è 4 mm (si sommano gli errori assoluti).
TABELLA 1
Fotocellula
Posizione
(x ¢ x) cm
Spostamento
¢ s (cm)
Tempo
(t ¢ t) (s)
Intervalli di tempo
¢ t (s)
F1
0
0
0
0
F2
¢s1 x 2 − x1 ¢t1 t2 − t1 F3
¢s2 x 3 − x 2 ¢t2 t3 − t2 F4
¢s3 x 4 − x 3 ¢t3 t 4 − t3 vm =
¢s
(m/s)
¢t
0
...
Ora puoi procedere con l’esperienza: azzera il cronometro, accendi il compressore e fai partire il carrello utilizzando il martelletto a molla che si trova all’inizio della rotaia.
Il carrello, passando davanti alla prima fotocellula, attiva il cronometro e vengono registrati i tempi di passaggio davanti alle fotocellule successive.
Riporta nella quarta colonna della tabella i tempi relativi a questi passaggi.
Riporta nella quinta colonna gli intervalli di tempo ¢t1 t2 − t1 , ¢t2 t3 − t2 ,...
relativi ai vari spostamenti.
¢s
Calcola infine il rapporto
, relativo a ciascun intervallo, annotando i valori trova¢t
ti nella sesta colonna della tabella 1.
Tale rapporto rappresenta la velocità media del carrello in ogni intervallo. L’incertezza sul valore della velocità media, considerato che si tratta di un rapporto, si
¢v
¢s
¢t
ottiene calcolando prima l’errore relativo
e poi moltiplicandolo
v
s
t
¢v
per v: ¢ v v
v
Costruisci un grafico della posizione in funzione del tempo, riportando sull’asse
delle ascisse il tempo e sull’asse delle ordinate la posizione. Ricordati di riportare
sul grafico anche le incertezze associate ai dati.
Ripeti più volte questo procedimento.
6
Risultato
Confronta i valori ottenuti per v e v e osserva su quale cifra incide l’errore. Arrotonda quindi il valore di v a quella cifra. Scrivi il risultato:
vm (...................... ; ......................) m/s
Osservando i grafici ottenuti, dovresti notare che i punti sono pressoché allineati.
Sebbene nei diversi grafici la pendenza della retta possa essere diversa, puoi osservare che si tratta ugualmente di un moto uniforme. In questo caso, la velocità media corrisponde alla velocità istantanea (pendenza della tangente alla curva).
Osservazioni
Probabilmente il grafico che hai ottenuto non è proprio lineare. Ciò è dovuto al fatto che, anche se la rotaia elimina
gran parte degli attriti, ancora si ha qualche resistenza al moto e quindi non si può dire che la risultante delle forze
che agiscono sul carrello sia effettivamente nulla.
Quesiti
• Se si allontanano fra loro le fotocellule, si ottengono misure più precise, meno precise o con la stessa precisione?
Giustifica la tua risposta.
7
LABORATORIO
5
Moto accelerato
Obiettivo
Svolgimento
Effettuare la misura della velocità e
dell’accelerazione media e istantanea
di un carrello che si muove su una
rotaia a cuscino d’aria inclinata.
Dopo aver montato l’apparato illustrato nel precedente laboratorio, inclina la rotaia di 5° rispetto all’orizzontale. Costruisci una tabella come quella mostrata di
seguito, riportando nella seconda colonna la posizione delle fotocellule, misurata
ponendo l’origine sulla prima fotocellula (F1).
Materiale occorrente
o Una rotaia a cuscino d’aria
o Un carrello
o Un’elettrocalamita
o Almeno 4 fotocellule
o Un cronometro digitale collegato
alle fotocellule (sensibile
al centesimo di secondo)
o Un compressore
o Un metro
o Un goniometro
Nella terza colonna riporta gli spostamenti ¢ s1 ⫽ x2 ⫺ x1, ¢ s2 ⫽ x3 ⫺ x2 , ...
o Fogli di carta millimetrata
Fotocellula
Posizione
(x ⫾ ¢x) cm
Spostamento
¢s (cm)
Tempo
(t ⫾ ¢t) (s)
Intervalli di tempo
¢t (s)
F1
0
0
0
0
F2
¢s1 ⫽ x 2 − x1 ⫽
¢t1 ⫽ t2 − t1 ⫽
F3
¢s2 ⫽ x 3 − x 2 ⫽
¢t2 ⫽ t3 − t2 ⫽
F4
¢s3 ⫽ x 4 − x 3 ⫽
¢t3 ⫽ t 4 − t3 ⫽
vm =
¢s
(m/s)
¢t
0
tm (s)
⌬tm (s)
0
0
am ⫽
¢vm
(m/s 2)
¢ tm
0
...
TABELLA 1
8
Per le incertezze puoi comportarti come per il laboratorio 4.
Procedi con l’esperienza: azzera il cronometro e fai aderire l’estremità del carrello
all’elettrocalamita montata sull’estremo più alto della rotaia. Fai partire il compressore e spegni l’elettrocalamita in modo che il carrello inizi a scendere.
Riporta nella quarta colonna della tabella i tempi rilevati dalle fotocellule e nella
quinta colonna gli intervalli di tempo ¢t1 ⫽ t2 − t1 , ¢t2 ⫽ t3 − t2 ,... relativi ai
vari spostamenti.
Nella sesta colonna riporta i valori delle velocità medie nei singoli intervalli.
Nella settima colonna scrivi il valore del tempo medio di ogni intervallo, definito
t ⫹ t2
come tm,1 ⫽ 1
, ...
2
Nell’ottava colonna scrivi gli intervalli di tempo calcolati tra i vari tempi medi successivi: ¢tm ,1 ⫽ tm , 2 ⫺ tm ,1, ...
Nella nona colonna scrivi i valori delle accelerazioni medie.
Costruisci ora il grafico della posizione in funzione del tempo, ponendo sull’asse delle ascisse il tempo e sull’asse delle ordinate la posizione, con le rispettive incertezze.
Costruisci il grafico della velocità in funzione del tempo, ponendo sull’asse delle
ascisse il tempo e sull’asse delle ordinate la velocità, con le rispettive incertezze.
Ripeti più volte questo procedimento e confronta i grafici ottenuti.
Ripeti l’intero procedimento inclinando la rotaia di 10° prima e poi di 15°, confrontando i grafici ottenuti.
Risultato
Osservando i grafici ottenuti, dovresti notare che i punti del grafico spazio-tempo
non sono allineati come nell’esperienza del laboratorio 4, ma, entro gli errori sperimentali, seguono un andamento parabolico con la concavità rivolta verso l’alto.
Nel grafico velocità-tempo, invece, i punti sono pressoché allineati, ovvero è possibile tracciare una retta entro le incertezze sperimentali. Ciò è indice di un’accelerazione costante.
Confrontando i grafici velocità-tempo relativi a inclinazioni diverse della rotaia,
dovresti notare che maggiore è l’inclinazione della rotaia, maggiore è la pendenza
della retta sul grafico, quindi maggiore è l’accelerazione.
Operando come al solito per le incertezze, scrivi i risultati ottenuti per le accelerazioni relative alle varie inclinazioni della rotaia:
a 5° ⫽ (...................... ⫾ ......................) m/s 2
a10° ⫽ (...................... ⫾ ......................) m/s 2
a15° ⫽ (...................... ⫾ ......................) m/s 2
Osservazioni
In questo caso la velocità istantanea può essere calcolata con il seguente procedimento:
– stabilito l’istante per cui si vuole calcolare la velocità, si individua il punto della curva spazio-tempo corrispondente e si traccia, per quel punto, la retta tangente alla curva;
– si determina la velocità istantanea interpretandola come la pendenza della tangente alla curva nel punto considerato.
Quesiti
• A quale grandezza corrisponde la pendenza della retta nel grafico velocità-tempo?
• Prendendo in considerazione il primo punto e l’ultimo dei grafici spazio-tempo e velocità-tempo, verifica la relazione a ⫽
v 2f − v 2i
.
2¢ x
• Riporta in tabella 2 gli spostamenti ¢ s1 , ¢ s2 , ¢ s3 , ... e i rispettivi intervalli di tempo ¢t1 , ¢t2 , ¢t3 , ... Calcola,
per ogni coppia di valori il rapporto
¢s
, riportando il risultato nella terza colonna della tabella.
¢t 2
TABELLA 2
¢ s (cm)
¢t (s)
¢s
(cm/s 2)
¢t 2
Che cosa ottieni? Interpreta i valori ottenuti nella terza colonna ricordando l’equazione del moto uniformemente ac1
celerato: s ⫽ at 2 .
2
9
LABORATORIO
6
Verifica della regola
del parallelogramma
Obiettivo
Svolgimento
Verificare che la composizione di due
vettori, in questo caso di due forze,
segue la regola del parallelogramma.
Lo schema di montaggio dell’apparato è mostrato in figura 1.
Appendi alcuni pesetti nel pun▼ FIGURA 1
to P, che è associato a un piccolo
cappio, e altri alle estremità libere del filo in modo che il sistema
risulti in equilibrio. Nel punto P,
in questo
modo,
agiscono tre
forze F3 , F1 ed F2 , la cui risultante è nulla.Ciò vuol
dire che
= 90°
F
la somma di
ed
F
2 è uguale e
1
opposta a F3 .
P
Quando il sistema è in equilibrio avvicina il foglio e riporta
su di esso la posizione del punto
P e alcuni punti che ti permettano di ricostruire la direzione dei
tre fili (che corrisponde alla direzione delle tre forze applicate
in P).
Traccia, dal punto P, le semirette che individuano la direzione delle tre forze. Lungo le tre direzioni individuate, traccia dei segmenti proporzionali, rispettivamente,
al numero di pesetti appesi alle estremità dei fili. Dovresti ottenere un disegno simile a quello mostrato in figura 2.
Materiale occorrente
o Alcuni pesetti
o Due aste e relative basi corredate
da pulegge
o Un sostegno per fogli e relativi
fogli da disegno
o Un righello
o Un goniometro
o Filo sottile di nylon
F1 + F2
e con il righello la
Misura con il goniometro l’ampiezza dell’angolo fra F1 ed F2 lunghezza della diagonale del parallelogramma che ha per lati F1 ed F2 .
Ripeti la procedura completa cambiando, di volta in volta, i pesi e compila la tabella 1.
F2
F1
TABELLA 1
P
0 F1 0 (N)
0 F2 0 (N)
0 F1 + F2 0 (N)
0 F3 0 (N)
F3
▲ FIGURA 2
Risultato
Dalla tabella
notare che il valore calcolato, attraverso la rappresentazione
dovresti
grafica, di 0 F1 + F2 0 , entro gli errori sperimentali, coincide con F3 . In altre parole, le
forze si sommano seguendo la regola del parallelogramma.
Osservazioni
Puoi notare che, se l’angolo fra F1 ed F2 è di 90°, le tre forze verificano il teorema di Pitagora e i loro moduli sono
una terna pitagorica.
Quesiti
• Descrivi quali sono le possibili cause di errore in questa esperienza.
• Se aumentiamo i pesi, l’influenza del peso del filo di nylon diminuisce, ma quale altra causa di errore aumenta?
• Che cosa succede se metti un ugual numero di pesetti alle estremità libere del filo? Descrivi la situazione.
10
LABORATORIO
7
Moto parabolico
Obiettivo
Svolgimento
Studiare il moto parabolico di un oggetto.
Monta l’apparato seguendo lo schema illustrato in figura.
È molto importante che la guida di accelerazione sia perpendicolare al bordo del
tavolo.
Materiale occorrente
o Una sfera metallica
h1
o Una guida di accelerazione per la
sfera
v0
o Un tavolo
o Fogli di carta carbone
h2
o Fogli da disegno
d
o Nastro adesivo
TABELLA 1
h1
h2
d
Misura l’altezza h1 del punto da cui parte la sfera sulla guida e l’altezza h2 del tavolo. Poni, alla base del tavolo, un foglio da disegno in una posizione tale che la sfera possa cadervi sopra.
Fissa con il nastro adesivo il foglio a terra. Poni sul foglio la carta carbone.
Ora, lascia cadere la sfera lungo la guida e rileva la distanza d, detta gittata (individuata attraverso il segno lasciato dalla carta carbone sul foglio), del punto di atterraggio sul foglio rispetto alla base del tavolo.
Esegui almeno 5 volte il procedimento, riportando sulla tabella 1 i dati raccolti.
Ripeti la prova cambiando l’altezza h1. Ripeti la prova cambiando l’altezza h2.
Risultato
Calcola la media dei valori trovati per d e associa come incertezza la semidispersione:
d (...................... ; ......................) cm
Confronta il risultato ottenuto con il valore teorico dteorico 2 h1 h2 . Tale valore
si ottiene considerando che la velocità finale di un corpo che scivola senza attrito
lungo un piano partendo da una altezza h1 è vf 2 gh1 .
Basta, a questo punto, impostare le equazioni del moto di un proiettile per ottenere la gittata d:
u
x vt
y 1 2
gt h2
2
da cui, ponendo x = d, y = 0 e v 2 gh1 , si ottiene dteorico 2 h1 h2 .
Osservazioni
I valori trovati per d dovrebbero avvicinarsi al valore teorico sempre di più a mano a mano che aumenti le altezze.
Ciò è dovuto al fatto che le perdite di velocità a causa degli attriti incidono meno, purché la velocità raggiunta sulla
guida non sia troppo alta e faccia perdere aderenza alla sferetta.
Quesiti
• Utilizzando il valore di d che hai trovato nella prima serie di misure, calcola la velocità della sfera al momento in cui
ha lasciato la guida e confrontala con la velocità teorica vteorica 2 gh1 .
11
LABORATORIO
8
Taratura di un dinamometro
Obiettivo
Svolgimento
Tarare una molla al fine di utilizzarla per
misurare il peso di un oggetto incognito.
La prova si svolge in tre fasi successive e ha
come prerequisito il fatto che forze uguali
producono allungamenti uguali della molla.
Materiale occorrente
Prima fase
La prima cosa che dovrai accertare è, quindi,
che i pesetti siano effettivamente uguali e che
producano allungamenti uguali. Lo schema di
montaggio dell’apparato è mostrato in figura.
Fissa il primo traguardo all’altezza dell’estremo inferiore della molla (a cui verranno appesi i pesetti). Appendi un pesetto e fissa il secondo traguardo all’altezza della nuova
posizione dell’estremo della molla. Misura la
distanza tra i traguardi. Cambia pesetto ed
esegui di nuovo la procedura controllando
che, entro gli errori sperimentali, l’allungamento sia sempre lo stesso.
Ora hai a disposizione un certo numero di pesetti uguali fra loro e puoi procedere con la taratura della molla.
o Una molla
o Vari pesetti uguali fra loro
o Un metro (sensibile al mm)
o Un’asta con due traguardi
o Un’asta alla quale appendere
una molla
o Carta millimetrata
o Un corpo di peso incognito
TABELLA 1
N. pesetti
Allungamento
1
2
3
...
Seconda fase
Appendi 2 pesetti e misura l’allungamento, poi appendine 3, poi 4 e così via, registrando in una tabella come la tabella 1 i valori ottenuti.
Costruisci un grafico sulla carta millimetrata, riportando sull’asse delle ascisse il
numero di pesetti e sull’asse delle ordinate il rispettivo allungamento. Valuta bene
l’incertezza e riportala sul grafico.
Potrai utilizzare il grafico che hai appena costruito per misurare il peso dell’oggetto incognito, utilizzando come unità di misura il “pesetto”.
Terza fase
Appendi l’oggetto incognito alla molla e misura l’allungamento che ne deriva.
Leggi sul grafico il numero di pesetti corrispondente all’allungamento del peso incognito (puoi utilizzare anche frazioni di pesetto se l’incertezza te lo consente).
Risultato
Il peso dell’oggetto incognito, espresso in unità “pesetto” è:
P (...................... ; ......................) pesetti
Osservazioni
Il grafico che hai ottenuto ha un intervallo di linearità, entro le incertezze sperimentali. Se continui ad aggiungere pesetti, l’allungamento non è più lineare e la molla si snerva. È evidente che la molla può essere utilizzata come misuratore di forze solo nella zona in cui l’allungamento è lineare.
Quesiti
• Descrivi un procedimento per convertire le misure effettuate in “pesetti” in newton ed esprimi il peso dell’oggetto incognito in newton.
12
LABORATORIO
9
Verifica della seconda legge
di Newton
Obiettivo
Svolgimento
Verificare che, se la risultante delle forze
che agiscono su un oggetto è diversa da
zero, l’oggetto accelera con una accelerazione direttamente proporzionale alla forza e inversamente proporzionale alla massa del sistema.
In figura è mostrato lo schema di montaggio dell’apparato.
Usa la livella per far sì che la rotaia sia perfettamente orizzontale.
Materiale occorrente
o Una rotaia a cuscino d’aria con
puleggia ed elettrocalamita
o Un carrello con portapesi
o Filo di nylon
L’esperienza è divisa in due fasi: nella prima si mantiene costante la forza e si aumenta la massa, verificando che l’accelerazione è inversamente proporzionale alla
massa; nella seconda fase, si mantiene costante la massa totale e si aumenta la forza, verificando che l’accelerazione è direttamente proporzionale alla forza.
o Un portapesi da attaccare al filo
di nylon
o Alcuni pesi noti
o Una livella a bolla
Prima fase
Metti sul portapesi del carrello un peso e annota il peso totale (carrello + peso).
Metti un peso nel portapesi attaccato al filo di nylon. Avvia il compressore, azzera
il cronometro e attacca il carrello alla elettrocalamita.
Spegni l’elettrocalamita e leggi i tempi sul cronometro. Riporta i dati in una tabella come quella sottostante e calcola l’accelerazione media, seguendo la metodologia utilizzata nel laboratorio 5.
Verifica che si tratta di un moto uniformemente accelerato.
o Almeno 4 fotocellule collegate
a un cronometro digitale
o Un metro (sensibile al mm)
TABELLA 1
Fotocellula
Posizione
(x ¢x) cm
Spostamento
¢s (cm)
Tempo
(t ¢t) (s)
Intervallo di tempo
¢t (s)
F1
0
0
0
0
vm =
¢s
¢t
0
tm (s)
tm (s)
0
0
am ¢vm
(m/s 2)
¢ tm
0
F2
F3
F4
...
TABELLA 2
Massa totale
Massa
(carrello +
Accelerazione
pesi + peso
Accelerazione
trainante)
Aggiungi un peso al carrello e calcola la nuova accelerazione. Ripeti più volte il
procedimento aggiungendo, di volta in volta, un peso al carrello.
Riporta nella tabella 2 le accelerazioni e la massa corrispondente, verificando che,
entro gli errori sperimentali, il prodotto della massa per l’accelerazione è costante.
Seconda fase
Avendo già verificato che si ottiene un moto uniformemente accelerato, basta disporre, in questo caso, di due fotocellule che segnalino i tempi di percorrenza di un
determinato spostamento. Conoscendo lo spostamento e il tempo, si può determi2¢ s
nare l’accelerazione utilizzando la relazione a 2 .
t
Basta, quindi, fissare le due fotocellule e misurare la loro distanza ¢s.
Metti alcuni pesi sul portapesi del carrello e un peso su quello attaccato al filo. Avvia il compressore, azzera il cronometro e attacca il carrello alla elettrocalamita.
Spegni l’elettrocalamita e leggi il tempo indicato dal cronometro.
13
TABELLA 3
Forza
Accelerazione
Ripeti la misura almeno 5 volte. Calcola la media dei valori trovati di t e associa,
come incertezza, il valore maggiore fra la sensibilità del cronometro e la semidispersione.
Scrivi il valore di t: t (...................... ; ......................) s
Sposta ora un peso dal carrello al portapesi attaccato al filo (in questo modo la
massa totale del sistema rimane costante, ma la forza trainante aumenta) e ripeti il
procedimento più volte, spostando, di volta in volta, un peso dal carrello al portapesi del filo.
Riporta nella tabella 3 la forza trainante e la corrispondente accelerazione.
Costruisci, sulla carta millimetrata, il grafico accelerazione-forza, mettendo sull’asse
delle ascisse l’accelerazione e sull’asse delle ordinate la forza.
Dovresti ottenere un grafico lineare, entro gli errori sperimentali. Di conseguenza
le grandezze in esame sono direttamente proporzionali e descritte da una legge
del tipo F = costante a. Il valore della costante di proporzionalità tra la forza e la
corrispondente accelerazione è dato dalla pendenza della retta.
Verifica che la costante di proporzionalità è uguale, entro gli errori sperimentali, alla massa totale del sistema.
Risultato
Prima fase
Mantenendo la forza costante si trova che il prodotto della massa per l’accelerazione
è costante. Utilizzando una forza costante F (...................... ; ......................) N abbiamo ottenuto le seguenti coppie di valori per m e a:
TABELLA 4
m (kg)
¢m (kg)
a (m/s2)
¢a (m/s2)
m a (N)
¢m a (N)
Il valore calcolato per ma coincide/non coincide, entro gli errori sperimentali con
la forza applicata.
Seconda fase
Mantenendo costante la massa, si trova che l’accelerazione è direttamente proporzionale alla risultante delle forze applicate al sistema.
Utilizzando una massa costante (massa del carrello massa dei pesi massa del
portapesi) m (...................... ; ......................) kg abbiamo ottenuto, al variare della forza applicata, le seguenti accelerazioni:
TABELLA 5
F (N)
¢F (N)
a (m/s2)
¢a (m/s2)
F
(kg)
a
F
¢ a b(kg)
a
F
Il valore calcolato di
coincide/non coincide, entro gli errori sperimentali con la
massa m del sistema. a
Osservazioni
Il grafico che hai ottenuto, probabilmente, non passa proprio per l’origine, come dovrebbe per una relazione di proporzionalità diretta. Ciò è dovuto agli attriti che, soprattutto nella fase iniziale del moto, non sono del tutto trascurabili.
Quesiti
• Quali grandezze hai misurato direttamente e quali indirettamente?
• Al diminuire della forza trainante, lo scostamento dal risultato teorico aumenta, diminuisce o rimane lo stesso?
14
LABORATORIO
10
Scomposizione della forza peso
in un piano inclinato
Carrucola 2
Obiettivo
Svolgimento
Determinare le componenti parallela e
perpendicolare della forza peso di un
corpo che si muove lungo un piano
inclinato.
Lo schema di montaggio del
l’apparato è mostrato in figura. Carrucola 1
N
Fissa, inizialmente, l’inclina
P2
zione del piano a 15°.
b
Dopo aver determinato con un P//
P
dinamometro
l’intensità della 1
a
forza peso P del carrello, apP⊥
pendi alcuni pesetti agli estreP
mi liberi dei fili di nylon attaccati al carrello in modo che il
a
sistema raggiunga l’equilibrio.
È importante che il filo attaccato al centro del carrello abbia direzione perpendicolare al piano inclinato (aiutati con una squadra per controllare l’angolo fra i fili).
Sotto questecondizioni, il diagramma delle forze è quello mostrato in figura:
la
forza peso P , la componente perpendicolare al
piano
della
forza
peso
P› e la
componente parallela al piano della forza peso P// , sono i lati di un triangolo rettangolo simile a quello
formato dal piano inclinato.
L’angolo fra P e P› è uguale all’angolo alla base del piano inclinato.
Dobbiamo verificare che:
P P sen e P› P cos
Materiale occorrente
o Un piano inclinato
con inclinazione regolabile
o Un carrellino
o Un’asta con carrucola
o Una carrucola da montare
alla sommità del piano inclinato
o Un metro
o Un goniometro e una squadra
o Filo di nylon
o Vari pesetti
o Carta millimetrata
Eseguiamo più volte l’esperienza, variando l’angolo di inclinazione del piano e riportiamo i valori di P e P› nella tabella 1.
Rappresenta in un grafico su carta millimetrata il valore di P (ordinata) in funzione dell’angolo (ascissa).
▲
TABELLA 1
P//
P›
Psen
Pcos
15°
20°
25°
30°
35°
40°
45°
Risultato
Dalla tabella dovresti constatare che effettivamente la relazione fra P , P// e P› è
quella che ci aspettavamo.
Osservazioni
Al posto dei pesetti attaccati al carrello mediante le carrucole, si possono utilizzare due dinamometri per avere una
lettura diretta delle forze. Puoi ripetere l’esperienza appesantendo il carrello e confrontando i risultati ottenuti con
quelli dell’esperienza precedente.
Quesiti
• Puoi dedurre dal grafico il valore dell’intensità di P// e P› per un angolo di 22°30’?
15
LABORATORIO
11
Stima dell’attrito dinamico
Obiettivo
Svolgimento
Determinare il coefficiente di attrito
dinamico fra due superfici che scorrono
l’una sull’altra.
Misura la massa del blocco A e del porta-pesi B. Usa la livella per assicurarti che il
piano sia orizzontale.
MA (...................... ; ......................) kg
M porta-pesi (...................... ; ......................) kg
Materiale occorrente
o Un piano con una superficie
levigata
A
o Una livella a bolla
o Una carrucola con morsetto
o Filo di nylon
o Un blocco di legno levigato a
forma di parallelepipedo
o Due fotocellule
o Un porta-pesi
o Alcuni pesi noti di differente entità
B
o Un metro (sensibile al mm)
o Un cronometro digitale
(sensibile al centesimo di secondo)
▲ FIGURA 1
o Una bilancia (meglio se digitale)
Dopo aver montato l’apparato rappresentato in figura 1, inizia a mettere alcuni pesi noti nel porta-pesi B. Noterai che il corpo A non si muove finché non si raggiunge un certo valore della forza trainante. Quando il blocco A inizia a muoversi, la
tensione del filo è uguale alla forza di attrito statico che agisce su A. Se si aumenta
il numero di pesi in B il sistema si muove di moto accelerato.
Se non ci fossero attriti, dalla teoria sappiamo che il sistema dovrebbe accelerare
F
con una accelerazione a =
, essendo F la risultante delle forze applicate. In queMtot
sto caso F è la forza peso in B, e Mtot è la massa totale del sistema MA + MB + Mpesi.
In realtà, tra la superficie del blocco e quella del piano, esiste una forza di attrito
dinamico che si oppone al moto. Ricordiamo che il coefficiente di attrito dinamico è definito come il rapporto fra la forza di attrito fd e la normale N al piano (in
questo caso uguale al peso MA g del blocco A):
fd
MA g .
Per determinare d devi calcolare
prima la forza di attrito che agisce
su A. Lo schema del corpo libero, in
questo caso, è quello mostrato in figura 2.
Possiamo scrivere le equazioni del
moto di questo sistema:
d =
e
T fd MA a
MBp g T MBp a
N
fd
T
A
Mag
T
A
▲ FIGURA 2
da cui, sommando e risolvendo rispetto a fd, otteniamo:
f d MBp g MABp a
16
M B+p i g
Le masse e l’accelerazione di gravità sono date, quindi ti basta determinare l’accelerazione del sistema per ottenere fd e, da questa, d.
Fissa le due fotocellule al piano, poni l’origine del tuo sistema di riferimento sulla
prima fotocellula e misura la posizione della seconda.
Poni il blocco A in corrispondenza dell’origine e lascialo partire, trainato dal peso
in B.
Rileva il tempo impiegato dal blocco A per passare dalla prima alla seconda fotocellula. Puoi calcolare l’accelerazione ricordando che, in un moto uniformemente
2¢ s
accelerato con partenza da fermo dall’origine, essa è a 2 .
t
Esegui la prova almeno 5 volte, riportando nella tabella sottostante il valore di ¢s,
t e a.
TABELLA 1
¢s
t
a =
2¢ s
t2
Calcola la media fra i valori di a ottenuti e associa come incertezza la semidispersione.
Sei ora in grado di calcolare fd e, quindi, d.
Risultato
La forza di attrito è:
f d (...................... ; ......................) N
Il coefficiente di attrito dinamico è:
fd
d (...................... ; ......................)
MA g
Osservazioni
È molto difficile stabilire con precisione il confine fra l’attrito statico (blocco ancora fermo) e l’attrito dinamico (blocco in movimento). Devi effettuare varie prove, utilizzando i pesi più leggeri che hai a disposizione, al fine di migliorare la tua misura.
Un’altra causa di errore è originata dal fatto che la legge utilizzata vale solo per un moto accelerato con partenza da
fermo. In effetti questa condizione non è del tutto assicurata, poiché esiste un margine di incertezza sulla posizione
del blocco quando viene avviata la prima fotocellula. Puoi stimare questa incertezza controllando manualmente l’intervallo delle posizioni entro le quali scatta la fotocellula.
Quesiti
• Dai dati in tuo possesso è possibile calcolare il coefficiente di attrito statico. Infatti la forza di attrito statico corrisponde alla tensione del filo, quando questa è appena sufficiente a far muovere il blocco. Ottieni il coefficiente di atfd
T
trito statico da s .
MA g
MA g
s (...................... ; ......................)
Confronta il valore ottenuto con quello dell’attrito dinamico e, se sono differenti, dai una spiegazione di questa differenza.
17
LABORATORIO
12
Determinazione del coefficiente
di attrito statico tra due superfici
Obiettivo
Svolgimento
Determinare il coefficiente di attrito
statico tra due superfici a contatto su
un piano a inclinazione variabile.
Predisponi l’apparato secondo lo schema mostrato in figura. Poni il blocco di legno
sul piano e incomincia a sollevare il piano molto lentamente. Noterai che esiste
un’inclinazione particolare raggiunta la quale il blocco inizia a scivolare. In queste
condizioni, misura l’altezza del piano e la base (distanza tra il piede della perpendicolare condotta dall’estremo alto del piano e il punto di appoggio).
Materiale occorrente
o Un blocco di legno levigato
a forma di parallelepipedo
o Un blocco di metallo
o Un piano la cui inclinazione possa
variare in modo continuo, dotato
di una superficie sulla quale
appoggiare i blocchi
h
a
o Un metro (sensibile al mm)
b
Il coefficiente di attrito statico fra le due superfici è uguale alla tangente trigonometrica dell’angolo di inclinazione del piano, quando il blocco inizia a scivolare. Questo valore è dato dal rapporto fra l’altezza e la base del piano in quella particolare
posizione.
h ...................... ; ...................... cm
b ...................... ; ...................... cm
h
s tan ......................
b
Per determinare l’incertezza da associare al coefficiente di attrito statico, ricordiamo che, per un rapporto, si sommano gli errori relativi, quindi:
¢
s
¢h
¢b
s
h
b
¢
s
¢
s s
s
Risultato
Il coefficiente di attrito statico fra la superficie del blocco di legno e quella del piano è:
s ...................... ; ......................
Osservazioni
Il coefficiente di attrito statico fra due superfici è una grandezza adimensionale. Essa, infatti, si ottiene dal rapporto
fra due lunghezze.
Quesiti
• Ti aspetti che il coefficiente di attrito fra il blocco di metallo e il piano sia maggiore, minore o uguale a quello fra il
blocco di legno e il piano? Verifica sperimentalmente la tua risposta.
• Se appoggi il blocco su un’altra faccia, di superficie maggiore, il coefficiente di attrito aumenta, diminuisce o rimane lo stesso?
18
LABORATORIO
13
Legge di Hooke
Obiettivo
Svolgimento
Verificare la relazione fra la forza applicata a una molla e il suo allungamento.
Dopo aver montato l’apparato mostrato in figura, utilizza una delle
due molle uguali e, dopo aver fissato il primo traguardo all’altezza dell’estremo inferiore della molla, appendi un pesetto, poi due e così via,
registrando, di volta in volta, la posizione dell’estremo inferiore della
molla.
Riporta in una tabella come quella
mostrata sotto i valori trovati e calcola la costante elastica k della
molla, secondo la relazione di
Hooke F = k ¢L.
Costruisci sulla carta millimetrata
il grafico forza-allungamento, riportando l’allungamento sull’asse delle ascisse e la forza sull’asse delle
ordinate.
Dovresti ottenere un grafico lineare
(entro gli errori sperimentali) la cui
pendenza (coefficiente angolare) è
la costante elastica k della molla.
Di conseguenza puoi affermare che
la forza è direttamente proporzionale all’allungamento della molla.
Materiale occorrente
o Varie molle, due delle quali uguali
o Un’asta con traguardi per misurare
gli allungamenti delle molle
o Un’asta alla quale appendere
le molle
o Un metro (sensibile al mm)
o Pesi vari di entità nota
o Carta millimetrata
TABELLA 1
Forza
Allungamento
...
...
k =
F
¢L
...
Risultato
La legge che esprime l’allungamento della molla in funzione della forza applicata è:
F = k ¢L
con k ...................... ; ...................... N/m .
Osservazioni
Se ripeti l’esperienza utilizzando le altre molle, ti accorgerai che la legge è sempre la stessa, cambia il valore della costante elastica k.
Quesiti
• Quanto vale la costante elastica se colleghi in serie le due molle uguali? E se le colleghi in parallelo?
Verifica sperimentalmente le tue risposte.
• La proporzionalità fra F e ¢L si mantiene aumentando il numero dei pesetti?
19
LABORATORIO
14
Verifica del teorema
delle “forze vive”
Obiettivo
Svolgimento
Effettuare una verifica sperimentale
del teorema dell’energia cinetica (o
delle “forze vive”).
Monta l’apparato mostrato in figura.
Materiale occorrente
o Una rotaia a cuscino d’aria dotata
di elettrocalamita e compressore
o Un carrello con porta-pesi
o Almeno due fotocellule
o Un metro (sensibile al mm)
o Una bilancia (meglio se digitale,
almeno al centesimo di grammo)
o Un cronometro digitale collegato
alle fotocellule (al centesimo di
secondo)
Traguardi ottici
Dispositivo
di sgancio
o Filo di nylon
o Porta-pesi
M A MB
g , dove MA è la massa
M A MB
del carrello e dei relativi pesi e MB è la massa del porta-pesi e dei relativi pesi. Questa
tensione, spostando il carrello di ¢s x2 x1, compie il lavoro L T ¢s. L’obiettivo della prova è verificare che questo lavoro è uguale alla variazione dell’energia
1
cinetica del carrello tra il punto 1 e il punto 2, ¢K = MA A v 22 v 21 B , come affer2
ma il teorema delle “forze vive”.
Misura le masse MA (carrello + relativi pesi) e MB (porta-pesi e relativi pesi):
Il carrello A è soggetto alla tensione del filo T =
o Alcuni pesi noti
MA (...................... ; ......................) kg
MB (...................... ; ......................) kg
da cui:
T
TABELLA 1
t1
t2
M A MB
g (...................... ; ......................) N
M A MB
Avendo fissato l’origine del sistema di riferimento nel punto di partenza del carrello (quando è attaccato alla elettrocalamita), misura la posizione delle due fotocellule, x1 e x2 :
x1 (...................... ; ......................) m
x2 (...................... ; ......................) m
Il lavoro compiuto da T, quando sposta il carrello da x1 a x2, è:
L T ¢ s (...................... ; .......................) J
Avvia ora il compressore e attacca il carrello alla elettrocalamita.
Spegni l’elettrocalamita e annota i tempi, t1 e t2, segnati rispettivamente al passaggio davanti alle fotocellule F1 e F2.
Esegui la prova almeno 5 volte e riporta i valori di t1 e t2 nella tabella a lato.
Calcola la media dei valori ottenuti, rispettivamente, per t1 e t2:
t1 (...................... ; ......................) s
t2 (...................... ; ......................) s
20
Supponendo che il moto sia uniformemente accelerato, puoi calcolare il valore delle velocità corrispondenti a s1 ed s2:
v1 =
2 x1
t1
e
v2 =
2 x2
t2
Quindi:
v1 (...................... ; ......................) m/s
v2 (...................... ; ......................) m/s
Puoi ora calcolare l’energia cinetica del carrello A negli istanti t1 e t2 e la variazione ¢K dell’energia cinetica subita dal carrello:
1
MA v 21 (...................... ; ......................) J
2
1
K 2 MA v22 (...................... ; ......................) J
2
K1 da cui:
¢ K K 2 K 1 (...................... ; .......................) J
Risultato
Confrontando i valori ottenuti, rispettivamente, per il lavoro L e per la variazione
dell’energia cinetica ¢K del carrello, possiamo affermare che, entro gli errori sperimentali, il teorema dell’energia cinetica è/non è verificato.
Nel caso in cui il teorema non sia verificato, quali possono essere le cause del risultato ottenuto?
Osservazioni
La misura più critica, in questa prova, è quella relativa ai tempi t1 e t2. In particolare, per attivare la fotocellula, viene utilizzato un oscuratore che, anche se piuttosto piccolo, ha dimensioni finite. È difficile stabilire la posizione esatta nella quale scatta la fotocellula e ciò si ripercuote sull’incertezza nella misura dei tempi che possono non corrispondere esattamente alle posizioni x1 e x2.
Quesiti
• Disponendo di una rotaia abbastanza lunga per poter aumentare le distanze x1 e x2, è probabile che la misura migliori, peggiori o rimanga la stessa?
21
LABORATORIO
15
Trasformazione dell’energia potenziale
di una molla in energia cinetica
Obiettivo
Svolgimento
Verificare che l’energia immagazzinata
in una molla compressa viene trasferita a un carrello sotto forma di energia cinetica.
Dopo aver montato la rotaia a cuscino d’aria ed esserti assicurato che sia orizzontale (usa la livella a bolla per questa operazione), misura la distanza fra le due fotocellule:
Materiale occorrente
o Una rotaia a cuscino d’aria
con compressore
o Un carrello con porta-pesi
¢ s (...................... ; .......................) m
Misura la posizione del carrello appoggiato alla molla, quando la molla è a riposo:
x0 (...................... ; ......................) m
Dopo aver avviato il compressore e azzerato il cronometro, spingi sul carrello,
comprimendo la molla, e misura la nuova posizione del carrello:
x1 (...................... ; ......................) m
o Qualche peso noto
o Una molla di costante elastica k
nota
Calcola l’energia elastica immagazzinata dalla molla:
1
U k ( ¢ x )2 (...................... ; ......................) J
2
o Una molla incognita
o Un cronometro digitale
(sensibile al centesimo di secondo)
collegato a due fotocellule
Lascia andare il carrello e annota i tempi t1 e t2 relativi al passaggio davanti alle
due fotocellule:
t1 (...................... ; ......................) s
t2 (...................... ; ......................) s
o Un metro (sensibile al mm)
o Una bilancia (meglio se digitale
almeno sensibile al centesimo
di grammo)
da cui:
o Una livella a bolla
Calcola la velocità media, che corrisponde a quella istantanea, trattandosi di un
moto uniforme:
¢s
v
(...................... ; .......................) m/s
¢t
Misura ora la massa del carrello (compresi gli eventuali pesi aggiunti):
¢t (...................... ; .......................) s
m (...................... ; ......................) kg
Calcola l’energia cinetica del carrello:
K
1
mv 2 (...................... ; ......................) J
2
Risultato
Dal confronto fra l’energia potenziale elastica e l’energia cinetica acquistata dal
carrello, risulta che, entro gli errori sperimentali, esse sono/non sono uguali.
Nel caso in cui le due grandezze non siano risultate uguali, quali potrebbero essere le cause della differenza tra le loro misure?
Osservazioni
Per migliorare l’affidabilità delle misure, puoi allontanare fra loro le fotocellule. In questo modo, l’errore relativo su
¢s e quello su ¢t diminuiscono. Per ottenere un buon risultato è preferibile utilizzare una molla con una costante elastica abbastanza piccola.
Quesiti
• Utilizzando il metodo appena descritto, calcola la costante elastica della molla incognita, misurando l’energia cinetica acquistata dal carrello e la compressione della molla.
22
LABORATORIO
16
Urto anelastico in una dimensione
Obiettivo
Svolgimento
Verificare la conservazione della quantità di moto in un urto anelastico.
Dopo aver montato l’apparato, facendo attenzione che il carrello sia orizzontale
(usa la livella per posizionare la rotaia), misura le distanze ¢s1 fra le fotocellule F1
ed F2, e ¢s2 fra le fotocellule F3 ed F4:
Materiale occorrente
¢ s1 (...................... ; .......................) m
o Una rotaia a cuscino d’aria
con compressore e martelletto
di spinta
¢ s2 (...................... ; .......................) m
o Due carrelli con meccanismo
di aggancio
o Un cronometro digitale
(sensibile al centesimo di secondo)
collegato a 4 fotocellule
o Una piccola quantità di plastilina
o Un metro (sensibile al mm)
o Una bilancia (meglio se digitale,
sensibile almeno al centesimo
di grammo)
Misura le masse dei carrelli M1 ed M2:
M1 (...................... ; ......................) kg
M2 (...................... ; ......................) kg
Carica la molla del martelletto di spinta e disponi i due carrelli, il primo appoggiato al martelletto, il secondo a metà strada fra le fotocellule F2 ed F3.
Avvia il compressore e azzera il cronometro. Mediante il martelletto, fai partire il
carrello 1.
Annota i tempi t1 e t2, relativi al passaggio del carrello 1 davanti alle fotocellule F1
ed F2 e i tempi t3 e t4 relativi al passaggio del convoglio dei due carrelli davanti alle fotocellule F3 ed F4:
t1 (...................... ; ......................) s
o Una livella a bolla
t2 (...................... ; ......................) s
o Una massa incognita
t3 (...................... ; ......................) s
t 4 (...................... ; ......................) s
Calcola ¢t1 t2 t1 e ¢t2 = t4 t3:
¢t1 (...................... ; .......................) s
¢t2 (...................... ; .......................) s
Calcola le velocità v1 =
¢ s1
¢ s2
e v2 =
:
¢ t1
¢t2
v1 (...................... ; ......................) m/s
v2 (...................... ; ......................) m/s
Infine puoi calcolare le quantità di moto prima dell’urto, p 1 M1 v1 e dopo
l’urto, p 2 ( M1 M2 ) v2
p 1 (...................... ; ......................) kg m/s
p 2 (...................... ; ......................) kg m/s
Risultato
Dal confronto fra p1 e p2 puoi affermare che la quantità di moto prima e dopo l’urto è/non è conservata.
Nel caso in cui le misure effettuate non ti consentano di verificare la conservazione della quantità di moto nell’urto anelastico, quali possono essere le cause che impediscono tale verifica?
Quesiti
• Aggiungi al carrello 2 la massa incognita e ripeti la prova determinandone l’entità.
23
LABORATORIO
17
Pendolo balistico
Obiettivo
Svolgimento
Determinare la velocità di un proiettile mediante il pendolo balistico.
In figura è mostrato uno schema dell’apparato costituito da una guida acceleratrice
allineata a un cassetto ricevitore. Il cassetto
è imbottito per evitare rimbalzi della biglia,
quando vi entra alla fine della sua corsa. Il
cassetto è appeso a quattro fili, che fanno in H
modo che possa oscillare, mantenendo una
posizione pressoché orizzontale.
Traguarda sulla carta millimetrata l’altezza
del cassetto nella sua posizione di equilibrio.
Posiziona la biglia sulla guida e misura l’altezza di partenza rispetto alla base:
Materiale occorrente
o Una guida acceleratrice
o Una biglia
o Un metro (sensibile al mm)
o Un pendolo balistico costituito
da un contenitore/ricevitore
imbottito appeso a quattro fili
h (...................... ; ......................) m
o Un foglio di carta millimetrata
Lascia cadere la biglia e annota la massima altezza H, rispetto alla posizione di
equilibrio, raggiunta dal pendolo in seguito all’urto anelastico con la biglia.
Ripeti almeno 5 volte la prova e calcola il valor medio di H.
Cambia l’altezza di partenza della biglia e riesegui la prova, riportando i valori di
h e di H nella tabella 1.
TABELLA 1
h
Calcola il rapporto
e riporta i valori calH
h
colati nella terza colonna della tabella.
h
H
H
Dovresti notare che tale rapporto, entro gli
errori sperimentali, rimane costante.
Per determinare la velocità della biglia,
quando entra nel carrello, basta applicare la
conservazione dell’energia meccanica e
uguagliare l’energia cinetica della biglia alla
fine della discesa, all’energia potenziale del
pendolo (carrello ricevitore + biglia), quando il pendolo ha raggiunto la sua massima altezza:
o Un sostegno verticale
per la carta millimetrata
1
m b v 2 ( m b mr ) gH
2
da cui:
TABELLA 2
h
H
v
¢v
2( m b + mr ) gH
mb
Devi, perciò, misurare le masse della biglia e del cassetto ricevitore mb e mr:
v
m b (...................... ; ......................) kg
mr (...................... ; ......................) kg
Risultato
Riporta nella tabella 2 le velocità corrispondenti alle varie altezze di partenza.
Osservazioni
Se si aumenta la massa della biglia si ottengono misure migliori, in quanto la biglia, a parità di velocità, raggiunge
un’altezza maggiore e quindi diminuisce l’errore relativo sull’altezza H.
Quesiti
• Confronta i valori calcolati di v per le varie altezze con quelli teorici ottenuti considerando la conservazione dell’energia meccanica all’inizio e alla fine della guida:
v 2 gh
24
h
LABORATORIO
18
Urto elastico
in una dimensione
Obiettivo
Svolgimento
Verificare la conservazione dell’energia
cinetica in un urto elastico.
Per misurare la velocità di un carrello mediante una fotocellula, devi montare il
traguardo rettangolare sul carrello in modo che, quando il carrello passa davanti
alla fotocellula, il traguardo avvii il cronometro, che rimane in funzione per tutto il
tempo in cui è interrotto il fascio di luce della fotocellula. Conoscendo la lunghezza del traguardo e il tempo che occorre perché passi davanti alla fotocellula, puoi
calcolare la velocità del carrello.
Per studiare l’urto elastico fra due carrelli devi montare come di consueto la rotaia
assicurandoti, con la livella, che sia orizzontale.
Devi misurare la massa dei due carrelli (compresi gli eventuali pesetti aggiunti) e
la lunghezza dei traguardi posti sui carrelli. Per effettuare quest’ultima operazione,
puoi porre il carrello davanti alla fotocellula e misurare le sue posizioni negli istanti in cui, rispettivamente, si attiva e si ferma il cronometro:
Materiale occorrente
o Una rotaia a cuscino d’aria dotata
di compressore e martelletto
di spinta
o Due carrelli con respingente
elastico, porta-pesi e traguardo
rettangolare
o Due cronometri digitali
(sensibile al centesimo di secondo)
collegati ciascuno a una
fotocellula
MA (...................... ; ......................) kg
x1A (...................... ; ......................) m
x2A (...................... ; ......................) m
o Un metro (sensibile al mm)
lA ¢ x x2 A x1A (...................... ; .......................) m
o Una bilancia digitale
(sensibile almeno
al centesimo di grammo)
MB (...................... ; ......................) kg
x1B (...................... ; ......................) m
o Alcuni pesi noti
x2B (...................... ; ......................) m
lB ¢ x x2 B x1B (...................... ; .......................) m
o Una livella a bolla
o Una massa incognita
Poni il carrello A all’estremità della rotaia, aderente al martelletto di spinta, e il carrello B tra le due fotocellule.
Quando esegui la prova, il carrello A, spinto dal martelletto, inizia a muoversi, attiva la prima fotocellula, urta contro il carrello B e, a seconda che la sua massa sia
maggiore, uguale o minore di questo, si possono avere tre casi:
– MA MB, i due carrelli si muovono nella stessa direzione e quindi dovrai registrare i tempi segnalati dalla seconda fotocellula;
– MA MB, il carrello A si ferma e il carrello B inizia a muoversi nella direzione
che aveva il carrello A; dovrai verificare che la velocità del carrello B sia uguale a quella che aveva il carrello A prima dell’urto;
– MA MB, il carrello A, dopo l’urto, inverte la direzione del moto.
Esegui una prova per ognuna delle tre situazioni descritte e riporta i tempi rilevati nella seguente tabella.
TABELLA 1
MA
MB
t1A
t2A
t1A
t2A
t1B
t2B
MA MB
MA MB
MA MB
Calcola, per ciascuna prova, le energie cinetiche di A e di B, rispettivamente prima
e dopo l’urto:
vA lA
(...................... ; ......................) m/s
t 2 A t1 A
v'A lA
(...................... ; ......................) m/s
t'2 A t'1A
25
da cui:
K A (...................... ; ......................) J
vB 0
KB 0
K'A (...................... ; ......................) J
lB
v'B (...................... ; ......................) m/s
t'2 B t'1B
K'B (...................... ; ......................) J
Sommando le energie cinetiche di A e di B, rispettivamente prima e dopo l’urto, ottieni:
K tot K A K B (...................... ; ......................) J
K'tot = K'A + K'B (...................... ; ......................) J
Risultati
Confrontando le energie totali prima e dopo l’urto puoi affermare che l’energia cinetica totale si è conservata/non si è conservata entro gli errori sperimentali.
Nel caso in cui l’energia cinetica non risulti conservata, discuti le possibili cause
d’errore.
Osservazioni
Con i dati che hai, puoi verificare anche la conservazione della quantità di moto.
Quesiti
• Aggiungi al carrello A la massa incognita e utilizza questa esperienza per determinarne l’entità.
26
LABORATORIO
19
Moto circolare uniforme
e accelerazione centripeta
Obiettivo
Svolgimento
Analizzare un moto circolare e determinare l’intensità della forza centripeta che agisce su un oggetto che si
muove di moto circolare uniforme.
Lo schema di montaggio dell’apparato è mostrato nella figura.
Dopo aver montato l’apparato e aver misurato la distanza R0, rispetto al centro di
rotazione, delle masse a riposo, accendi il motore e, gradualmente, fai aumentare il
numero di giri. Potrai notare che, superata una certa velocità, non sei più in grado
di distinguere chiaramente la barra che ruota, ma ti appare come un cerchio pieno.
Posiziona ora la lampada stroboscopica al di sopra dell’apparato, in modo da illuminarlo. È preferibile oscurare un po’ l’ambiente per facilitare l’osservazione.
Accendi la lampada e regola la sua frequenza fino a che non vedi la barra quasi
ferma. Raggiunta questa situazione, puoi affermare che la frequenza del moto della barra è uguale alla frequenza della lampada.
Fissata la frequenza, misura la distanza dal centro delle masse attaccate alle molle.
Se le molle e le masse sono uguali, basta misurare la distanza tra le due masse e dividere il risultato per 2. Tale distanza corrisponde al raggio del moto circolare compiuto da ciascuna massa.
Conoscendo la frequenza f e il raggio R, è possibile calcolare tutte le grandezze cinematiche del moto di ciascuna massa. Si ha, infatti:
v2
acp 2 R 2f
v R
R
Ripeti lo stesso procedimento, facendo variare di volta in volta la frequenza di rotazione del motore. Riporta i risultati ottenuti nella tabella 1.
Materiale occorrente
o Un motore elettrico a velocità
variabile
o Una barra graduata con guida,
da agganciare al motore
o Coppie di masse uguali
che scorrano nella guida
della barra graduata
o Due molle uguali, di costante
elastica k nota, per collegare le
masse al centro della piattaforma
o Un metro (sensibile al mm)
o Una bilancia (meglio se digitale)
o Una lampada stroboscopica con
frequenza variabile
Motore
TABELLA 1
f
R
v
acp
Misura ora la massa dei corpi attaccati alle molle. Moltiplicando la massa per l’accelerazione centripeta ottieni la forza centripeta Fcp applicata a ciascuna massa. Riporta in
tabella 2, per ciascuna frequenza, la forza centripeta così calcolata e confrontala con la
forza elastica Fe k (R R0), esercitata dalle molle, corrispondente a quella frequenza.
TABELLA 2
f
R
acp
Fcp
Fe
Risultato
La forza centripeta e la forza elastica calcolate in questa esperienza coincidono/non
coincidono entro gli errori sperimentali.
Osservazioni
Questa esperienza presenta molte criticità per la complessità dell’apparato e per la difficoltà della stima dell’incertezza da associare ad alcune misure, in particolare la frequenza f e la distanza R dal centro. Non è raro, quindi, che ci sia
un forte scarto fra la forza centripeta e la forza elastica.
Quesiti
• Se raddoppi la massa attaccata alle molle, di quanto varia il raggio della circonferenza percorsa dalle masse? Verifica sperimentalmente la tua risposta.
27
LABORATORIO
20
Confronto fra oggetti che rotolano
(senza strisciare) su un piano inclinato
Obiettivo
Svolgimento
Valutare la differenza di comportamento fra un cilindro pieno e uno cavo
che rotolano su un piano inclinato.
Assicurati che le superfici a contatto
(piano e cilindri) non scivolino l’una
sull’altra.
Puoi ottenere un migliore funzionamento dell’apparato se almeno una
delle due superfici (piano o cilindro)
è gommata.
Misura la massa dei due cilindri:
Materiale occorrente
o Un piano inclinato
o Due cilindri, uno pieno (1)
e uno cavo (2),
con lo stesso raggio
e la stessa massa
(possono avere altezze diverse)
o Un calibro
o Un metro (sensibile al mm)
o Un cronometro (sensibile
al centesimo di secondo)
2
M1 (...................... ; ......................) kg
Misura il raggio dei due cilindri:
1
M2 (...................... ; ......................) kg
R1 (...................... ; ......................) m
R2 (...................... ; ......................) m
Calcola il momento di inerzia dei due cilindri:
1
I 1 M1 R12 (...................... ; ......................) kg m 2
2
I 2 M2 R22 (...................... ; ......................) kg m 2
o Una bilancia digitale (sensibile
almeno al centesimo di grammo)
Inclina leggermente il piano. Misura l’altezza dalla quale farai partire i cilindri e la
lunghezza del percorso del cilindro sul piano:
h (...................... ; ......................) m
l (...................... ; ......................) m
Lascia andare un cilindro alla volta e misura il tempo che occorre affinché rotoli fino in fondo.
Ripeti la prova, variando l’altezza del piano, e riporta i valori ottenuti per il tempo
nella tabella 1.
TABELLA 1
h
l
¢t1
¢t2
v1
v2
Costruisci un grafico, riportando, per ogni altezza del piano, sull’asse delle ascisse
la velocità del cilindro 1 e sull’asse delle ordinate quella del cilindro 2.
Risultato
Il rapporto fra le velocità dei due cilindri è/non è costante entro gli errori sperimentali. Se il rapporto è costante, il suo valore è:
v2
(...................... ; ......................)
v1
Osservazioni
La relazione fra v1 e v2 dovrebbe essere lineare e il rapporto che hai calcolato dovrebbe essere uguale a
Ciò è coerente con il fatto che il momento di inerzia del cilindro pieno è minore di quello del cilindro cavo.
Quesiti
• Dimostra che
28
v2
v1
3
.
2
3
.
2