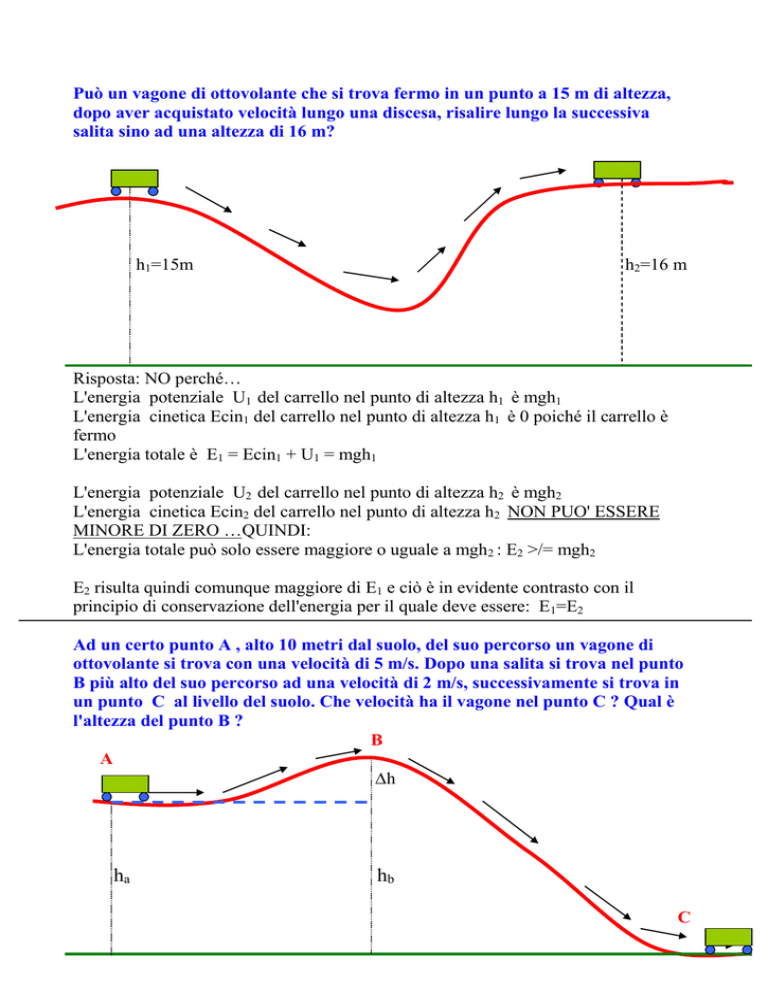
Può un vagone di ottovolante che si trova fermo in un punto a 15 m di altezza,
dopo aver acquistato velocità lungo una discesa, risalire lungo la successiva
salita sino ad una altezza di 16 m?
h1=15m
h2=16 m
Risposta: NO perché…
L'energia potenziale U1 del carrello nel punto di altezza h1 è mgh1
L'energia cinetica Ecin1 del carrello nel punto di altezza h1 è 0 poiché il carrello è
fermo
L'energia totale è E1 = Ecin1 + U1 = mgh1
L'energia potenziale U2 del carrello nel punto di altezza h2 è mgh2
L'energia cinetica Ecin2 del carrello nel punto di altezza h2 NON PUO' ESSERE
MINORE DI ZERO …QUINDI:
L'energia totale può solo essere maggiore o uguale a mgh2 : E2 >/= mgh2
E2 risulta quindi comunque maggiore di E1 e ciò è in evidente contrasto con il
principio di conservazione dell'energia per il quale deve essere: E1=E2
Ad un certo punto A , alto 10 metri dal suolo, del suo percorso un vagone di
ottovolante si trova con una velocità di 5 m/s. Dopo una salita si trova nel punto
B più alto del suo percorso ad una velocità di 2 m/s, successivamente si trova in
un punto C al livello del suolo. Che velocità ha il vagone nel punto C ? Qual è
l'altezza del punto B ?
B
A
h
ha
hb
C
Scegliamo il livello di terra (linea verde) come livello zero per l'energia potenziale.
La velocità nel punto C si trova imponendo il principio di conservazione dell'energia
fra i punti A e C:
1/2 mva2 + mgha = 1/2 mvc2 (il secondo membro non ha il termine di energia
potenziale perché nel punto C quest'ultima è nulla)
da cui si ricava :
vc2 - va2 = 2gha e, sostituendo i valori ai simboli:
vc2 = 25 + 2·9,8·10 = 25+196 =221
da cui:
vc= 14,87 m/s
Scegliamo adesso per comodità il livello del punto A come livello zero
dell'energia potenziale (linea tratteggiata blu). Il punto B così risulta ad
una altezza h.
Applicando il principio di conservazione dell'energia fra i punti A e B possiamo
ricavare h:
1/2 mva2 =1/2 mvb2 +mgh (il primo membro non ha il termine di energia
potenziale perché con la nuova scelta del livello di riferimento l'energia potenziale in
A è nulla)
da qui otteniamo per h :
h= 1/2(va2 - vb2)/g e, sostituendo i valori ai
simboli: h= 0,5·(25-4)/9,8 =1,07 m
Il punto B è quindi ad una altezza di 11,07 m dal suolo
Un vagoncino di massa 200 Kg scivola su una rotaia diottovolante dauna
altezza di 10 m e viene fermato in seguito ad un urto con un respingente
ancorato ad una grossa molla la cui costante elastica è K .
Stabilire quanto deve valere la costante K della molla se si vuole che il
vagone venga arrestato comprimendo la molla di 1 m.
H=10m
L'energia potenziale del carrello e Ug= mgh = 200·9,8·10 = 20000 J
Se nel punto più alto il carrello è fermo, la sua energia cinetica è zero
pertanto l'energia totale del carrello è pari alla sola energia potenziale
E=20000J.
Alla fine della discesa e prima di urtare la molla, la sua energia (sempre
uguale a 20000 J) sarà soltanto energia cinetica perché l'energia potenziale
gravitazionale è ridotta a zero.
Successivamente, quando il carrello ha compresso la molla sino a fermarsi
l'energia cinetica è ridotta a zero e l'enria totale (sempre di 20000 J) è
soltanto il termine di energia potenziale elastica di compressione della
molla Ue= 1/2·K·x2 dove x è la compressione (o allungamento) della
molla.
Il problema allora si risolve eguagliando le due espressioni dell'energia
potenziale all'inizio e alla fine del percorso (essendo in entrambi i casi
l'energia cinetica nulla)
mgh =1/2·K·x2
da cui: K= 2mgh/x2
quindi, sostituendo i valori numerici:
K=40000/12 = 4·104 N/m












