Energia potenziale
L’energia potenziale elettrostatica è una funzione della posizione tale che la sua variazione (tra due
punti del campo) cambiata di segno uguaglia il lavoro compiuto dalle forze del campo per portare la
carica dal primo al secondo punto. Tale funzione esiste in quanto il lavoro compiuto non dipende
dal percorso effettuato dalla carica, ma solo dalla posizione iniziale e dalla posizione finale, cioè in
quanto il campo elettrico statico è un campo conservativo. Tale funzione è definita a meno di una
costante additiva.
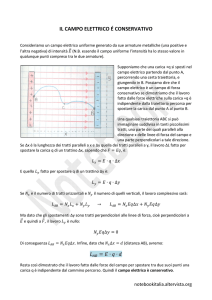
Caso del campo elettrico uniforme:
Si verifica facilmente che il campo è conservativo.
Infatti, per portare una carica q da A a B lungo il
segmento AB il lavoro è:
C
A
B
L = F ⋅ AB = qE ⋅ ∆s
mentre lungo il percorso passante per C è:
AB
cos α = F ⋅ AB = qE ⋅ ∆s
cos α
cioè il lavoro compiuto non dipende dal percorso effettuato dalla carica.
L = F ⋅ AC cos α + F ⋅ BC cos 90° = F ⋅
r
Introducendo un livello di riferimento (linea r)
perpendicolare alle linee di forza ed indicando
con xA la distanza di A da esso e con xB la
distanza di B da esso, risulta:
L = qEx A − qExB
A
B
Si può dunque introdurre la funzione U ( x ) = qEx e scrivere:
L = U ( x A ) − U ( x B ) = −∆U
Anche la funzione U ( x ) = qEx + k soddisfa la condizione L = − ∆U (come si può facilmente
verificare). Tuttavia importa la variazione di questa funzione (che è legata al lavoro) e tale
variazione non dipende dal particolare k. Scegliere un diverso valore di k equivale a fissare il livello
di riferimento in un’altra posizione.
Caso del campo elettrico centrale:
Anche il campo elettrico generato da una carica puntiforme è conservativo. Si dimostra che il lavoro
compiuto per portare una carica q da un punto A ad un punto B risulta in questo caso dato dalla
espressione:
1 Qq
1 Qq
L=
⋅
−
⋅
4πε rA 4πε rB
1 Qq
Si può quindi introdurre la funzione U ( r ) =
e scrivere:
⋅
4πε r
L = U (rA ) − U (rB ) = −∆U
Il potenziale elettrostatico
Il potenziale elettrostatico V in un punto è il rapporto tra l’energia potenziale di una carica q posta
U
in quel punto e la carica stessa: V = .
q
E’ quindi una grandezza scalare.
E’ una caratteristica del campo in quanto non dipende dalla carica di prova.
Dipende evidentemente dal livello di riferimento dell’energia potenziale, tuttavia ciò che importa è
la differenza di potenziale (d.d.p.) tra due punti del campo e questa non dipende dal livello di
riferimento, ma solo dalla posizione dei due punti.
U A − U B LAB
=
da cui
LAB = q (VA − VB )
q
q
LAB è il lavoro compiuto dalle forze del campo per portare la carica q da A a B; pertanto la d.d.p tra
A e B è uguale al lavoro compiuto dalle forze del campo per portare la carica unitaria dal punto A al
punto B.
Cariche positive vengono spinte dalle forze del campo da punti a potenziale maggiore verso punti a
potenziale minore.
La d.d.p. si misura in Volt (V), quindi tra due punti A e B c’è la differenza di potenziale di 1 V se le
forze del campo compiono un lavoro di 1 J per portare la carica di 1 C da A a B.
VA − VB =
In particolare risulta:
∆U
qExB − qEx A
VA − VB = −
=−
q
q
VA − VB = −
∆U
Q 1
1
=−
−
q
4πε 0 xB x A
per un campo elettrico uniforme
per un campo elettrico centrale
Relazione tra campo elettrico e potenziale
Caso del campo elettrico uniforme:
U − U B qEx A − qExB
VA − VB = A
=
= E ( x A − xB )
A
B
q
q
da cui:
V −V
∆V
∆V
E= A B =−
=−
x A − xB
∆s
AB
E ha la direzione perpendicolare alle superfici equipotenziali.
E ha il verso che va da punti a potenziale maggiore verso punti a potenziale minore.
r
Caso di un campo elettrico qualunque:
Pur di considerare un volumetto molto piccolo, il campo elettrico può essere considerato uniforme
in esso. Pertanto per un campo elettrico qualunque, supponendo i punti A e B sufficientemente
∆V
vicini, risulta: E = −
con ∆s estremamente piccolo.
∆s