Alcune applicazioni delle equazioni differenziali ordinarie alla teoria

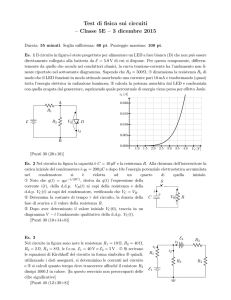
Alcune applicazioni delle equazioni differenziali
ordinarie alla teoria dei circuiti elettrici
Attilio Piana, Andrea Ziggioto
1
1.1
Regime variabile in un circuito elettrico.
Circuito RC.
Carica del condensatore
Consideriamo un circuito di resistenza R e capacità C, alimentato da un
generatore di forza elettromotrice costante E0 , di resistenza interna trascurabile. Supponiamo che il circuito sia inizialmente aperto. Si supponga inoltre
che il condensatore sia inizialmente completamente scarico. Si vuole studiare
il comportamento del circuito dopo che all’istante iniziale t = 0 esso sia stato
chiuso.
Indichiamo con VR (t) la tensione ai capi della resistenza R al tempo t.
Sappiamo che, detta i(t) l’intensità di corrente ai capi del condensatore al
tempo t, si ha
VR (t) = Ri(t).
(1)
Indicando con q(t) la carica del condensatore al tempo t e con VC (t) la
tensione ai capi del condensatore, sappiamo anche che
q(t) = CVC (t).
Derivando la (2) rispetto al tempo t e ricordando che i(t) =
i(t) =
dVC
dq
=C
= CVC0 (t).
dt
dt
Allora la legge di Ohm generalizzata
VR + VC = E0
1
(2)
dq
,
dt
otteniamo
(3)
diventa, usando la (1) e la (3),
RC VC0 + VC = E0 .
(4)
La (4) è un’equazione differenziale del primo ordine a variabili separabili che
diventa, dividendo ambo i membri per RC,
1
dVC
=−
dt.
VC − E0
RC
Integrando ambo i membri otteniamo
log(VC − E0 ) = −
1
t + c,
RC
da cui
c∈R
1
VC (t) = E0 + k e− RC t ,
avendo posto k = ec .
Imponendo la condizione iniziale
VC (0) = 0
troviamo k = −E0 , da cui
³
1
− RC
t
´
VC (t) = E0 1 − e
(5)
Derivando la (5) otteniamo
VC0 (t) = E0
1 − 1 t
e RC
RC
(6)
e, sostituendo la (6) nella (3), ricaviamo infine
i(t) =
E0 − 1 t
e RC ,
R
che rappresenta l’intensità di corrente di carica del condensatore (vedere
Figura 1).
2
i(t)
O
t
Figura 1: Corrente di carica del condensatore in RC
1.2
Scarica del condensatore
Se un condensatore di capacità C, caricato con una tensione E0 , viene posto
in un circuito comprendente una resistenza complessiva R e se all’istante
t = 0 si chiude il circuito, il condensatore si scarica sulla resistenza.
Poichè nel circuito non esistono f.e.m. dovute a generatori, le tensioni ai
capi del condensatore e della resistenza devono essere uguali:
VC = VR .
Se i(t) è l’intensità di corrente ai capi del condensatore all’istante t, ricordando che
dq
i(t) = − = −C VC0 (t)
(7)
dt
e che
VR = Ri = −RCVC0 ,
abbiamo
VC = −RCVC0 .
Anche questa è un’equazione differenziale del primo ordine a variabili separabili. Otteniamo
dVC
1
=−
dt.
VC
RC
3
Integrando membro a membro abbiamo
log VC (t) = −
1
t + c,
RC
da cui
c∈R
1
VC (t) = ke− RC t
avendo posto k = ec . Imponendo la condizione iniziale
VC (0) = E0
ricaviamo
1
VC (t) = E0 e− RC t .
Ricavando VC0 (t) e inserendola nella (3) possiamo ottenere l’andamento dell’intensità di corrente di scarica del condensatore (vedere Figura 2):
i(t) =
E0 − 1 t
e RC
R
i(t)
O
t
Figura 2: Corrente di scarica del condensatore in RC
4
2
Regime variabile in un circuito elettrico.
Circuito RL.
2.1
Circuito RL con forza elettromotrice costante
Consideriamo un circuito di resistenza R, induttanza L, alimentato da un
generatore di forza elettromotrice costante E0 , di resistenza interna trascurabile. Scriviamo la legge di Ohm generalizzata, indicando con i = i(t)
l’intensità della corrente all’istante t. Si ha
L
di
+ Ri = E0 .
dt
Questa è un’equazione differenziale del primo ordine a variabili separabili.
Possiamo quindi separare le variabili e ottenere
L
di = dt
E0 − Ri
da cui, integrando membro a membro, otteniamo
−
cioè
L
log(E0 − Ri) = t + c,
R
c ∈ R,
R
log(E0 − Ri) = − (t + c)
L
da cui
R
E0 − Ri = ke− L t ,
−R
c
L
con k = e
(8)
. Da questa uguaglianza si ricava
R
E0 − ke− L t
i(t) =
.
R
Poichè si sa che, quanto è t = 0, anche i = 0, dalla (8) si deduce che
0=
E0 − ke0
,
R
da cui k = E0 . Quindi, sempre dalla (8), si ottiene l’espressione dell’intensità
di corrente:
´
E0 ³
−R
t
L
1−e
.
i(t) =
R
5
R
Osservazioni. Osserviamo che il termine e− L t tende a 0 con l’aumentare
del tempo t e tanto più rapidamente quanto più piccola è l’induttanza L.
Il diagramma della corrente in Figura 3 mostra che l’intensità della corrente, alla chiusura del circuito, non raggiunge subito il valore di regime
i0 = ER0 , ma cresce esponenzialmente tendendo al valore i0 ; se l’induttanza L
del circuito è molto piccola, il circuito raggiunge il valore di regime in breve
tempo.
i
i
0
t
O
Figura 3: RL con E0
R
Il termine i1 = −i0 e− L t si chiama extracorrente di chiusura del
circuito.
2.2
Circuito RL senza forza elettromotrice
Dopo che la corrente nel circuito ha raggiunto il valore di regime i0 , supponiamo di escludere il generatore di forza elettromotrice costante E0 , chiudendo
il circuito direttamente su R e L. La presenza dell’induttanza L determina
una forza elettromotrice autoindotta che fa circolare nel circuito una corrente, detta extracorrente di apertura, che può essere calcolata risolvendo
l’equazione differenziale
di
L + Ri = 0,
dt
ottenuta applicando la legge di Ohm con E0 = 0.
Questa è nuovamente un’equazione differenziale del primo ordine a variabili separabili, il cui integrale generale è
R
i(t) = ce− L t ,
6
c ∈ R.
(9)
Tenendo presente che all’istante t = 0, in cui è stato escluso il generatore,
la corrente aveva intensità i0 , si ottiene il valore della costante arbitraria c;
infatti si ha
i0 = c · e0 = c.
Pertanto la (9) può scriversi come
R
i(t) = i0 e− L t .
L’extracorrente di apertura decresce rapidamente con legge esponenziale e
dopo breve tempo è difficilmente valutabile (Figura 4).
i
i0
t
O
Figura 4: RL senza E0
2.3
Circuito RL con forza elettromotrice alternata
Consideriamo un circuito di resistenza R, induttanza L, alimentato da un
generatore di f.e.m. alternata E sin ωt. Applicando la legge di Ohm generalizzata possiamo scrivere
L
di
+ Ri = E sin ωt.
dt
(10)
La (10) è un’equazione differenziale del primo ordine lineare, che può scriversi
come
E
R
i0 + i = sin ωt,
L
L
7
il cui integrale generale è dato da
½Z
R
R
E
− R
dt
i(t) = e L
sin ωt e
L
da cui
½
i(t) = e
−R
t
L
E
L
¾
R
L
dt
dt + c1 ,
¾
Z
sin ωt e
R
t
L
dt + c1 .
(11)
Calcoliamo a parte l’integrale
Z
I=
R
sin ωt e L t dt.
R
R
Poniamo f (t) = e L t e g 0 (t) = sin ωt. Allora f 0 (t) = R
e L t e g(t) = − ω1 cos ωt.
L
Integrando per parti abbiamo
Z
R
1 Rt
R
cos ωt e L t dt.
I = − e L cos ωt +
ω
Lω
R
R
Poniamo f (t) = e L t e g 0 (t) = cos ωt. Allora f 0 (t) = R
e L t e g(t) = ω1 sin ωt.
L
Integrando nuovamente per parti otteniamo:
½
¾
Z
R
1 Rt
R 1 Rt
R
t
I = − e L cos ωt +
sin ωt e L dt =
e L sin ωt −
ω
Lω ω
Lω
R Rt
R2
1 R
L sin ωt −
= − e L t cos ωt +
e
I.
ω
Lω 2
L2 ω 2
In questo modo otteniamo che
µ
¶
¶
¶
R µ
R µ
R2
eLt R
eLt R
1+ 2 2 I =
sin ωt − cos ωt = 2
sin ωt − ω cos ωt .
Lω
ω
Lω
ω
L
e con qualche semplice passaggio algebrico abbiamo (a meno di una costante
arbitraria)
¶
µ
µ
¶
R
R
eLt
R
R sin ωt − ωL cos ωt
eLt
sin ωt − ω cos ωt
I=
.
2 =
ω 2 L2 +R2
L
L
ω2 + R
L2
L2
(12)
Sostituendo la (12) nella (11) si ha
i(t) =
R
E
(R sin ωt − ωL cos ωt) + c1 e− L t .
2
+R
ω 2 L2
8
(13)
Tenendo conto della condizione iniziale i = 0 per t = 0, si ottiene il valore
della costante arbitraria c1 :
0=
E
(−ωL) + c1
+ R2
ω 2 L2
da cui
c1 =
E
ωL.
+ R2
ω 2 L2
La (13) può cosı̀ riscriversi come
´
³
E
t
−R
L
i(t) = 2 2
R
sin
ωt
−
ωL
cos
ωt
+
ωL
e
.
ω L + R2
Ponendo
def
Z =
√
(14)
ω 2 L2 + R2 ,
grandezza che viene detta, per un circuito ohmico-induttivo, impedenza e
corrisponde alla resistenza dei circuiti in corrente continua, abbiamo
µ
¶
E R
ωL
ωLE − R t
i(t) =
sin ωt −
cos ωt +
e L .
(15)
Z Z
Z
Z2
Poniamo ora
R def
ωL def
= cos ϕ,
= sin ϕ,
Z
Z
osservando che tale posizione è giustificata dall’essere
cos2 ϕ + sin2 ϕ =
(16)
R2 ω 2 L2
R2 + ω 2 L2
R2 + ω 2 L2
+
=
=
= 1,
Z2
Z2
Z2
R2 + ω 2 L2
e sostituiamo nella (15), ottenendo
i(t) =
E
ωLE − R t
(sin ωt cos ϕ − cos ωt sin ϕ) +
e L ,
Z
Z2
da cui
i(t) =
E
ωLE R
sin(ωt − ϕ) + 2 e− L t .
|Z
{z
} | Z {z }
i1
(17)
i2
In Figura 5 si può vedere l’andamento di i(t). Si è cosı̀ ottenuto che
l’intensità i(t) della corrente che attraversa il circuito è la somma del termine
i1 =
ωLE − R t
e L ,
Z2
9
i
O
t
Figura 5: RL con f.e.m. alternata
che decresce esponenzialmente con il tempo, e del termine
i2 =
E
sin(ωt − ϕ),
Z
che rappresenta l’andamento della corrente in condizione di regime: i2 ha
andamento sinusoidale ed è in ritardo rispetto alla tensione alternata del
generatore. L’angolo ϕ, detto angolo di sfasamento tra la tensione e la corrente, è compreso fra 0 e π2 perchè, per le posizioni prima fatte in (16), sin ϕ
e cos ϕ sono entrambi positivi.
3
Regime variabile in un circuito elettrico.
Circuito RLC
Consideriamo ora il caso di un circuito elettrico contenente una resistenza R,
un’induttanza L e un condensatore di capacità C. Supponiamo che all’istante
iniziale t = 0 in cui il circuito viene chiuso vi sia la carica q0 sulle armature
del condensatore.
Vogliamo studiare l’intensità i = i(t) della corrente di scarica del condensatore.
Indicando con V1 − V2 la differenza di potenziale esistente tra le armature
del condensatore all’istante t, l’armatura a potenziale maggiore possiede la
carica
q = q(t) = C(V1 − V2 ),
10
da cui
q
.
(18)
C
L’intensità della corrente i(t) che circola a spese della scarica del condensatore
è data da
dq
i(t) = − .
(19)
dt
Per la legge di Ohm generalizzata si ha
V1 − V2 =
V1 − V2 − L
di
= Ri.
dt
Ricordando la (18) e la (19), otteniamo
L
d2 q
dq
1
+R
+ q = 0.
2
dt
dt C
(20)
Si ottiene cosı̀ un’equazione differenziale lineare del secondo ordine omogenea
a coefficienti costanti.
L’equazione caratteristica associata alla (20) è
L λ2 + R λ +
1
= 0.
C
(21)
Il discriminante ∆ della (21) è allora
L
∆ = R2 − 4 .
C
Potranno cosı̀ presentarsi 3 diversi casi, a seconda del segno del discriminante
∆.
3.1
q
∆ > 0 =⇒ R > 2 CL
L’equazione (21) ammette due radici reali, entrambe negative, che indichiamo
con λ1 = −α e λ2 = −β (α, β > 0).
L’integrale generale è
q(t) = c1 e−αt + c2 e−βt
da cui
i(t) = −
dq
= α c1 e−αt + β c2 e−βt ,
dt
11
dove le costanti arbitrarie c1 e c2 si determinano in base alle condizioni iniziali:
q(0) = q0 ,
Si ha cosı̀
(
da cui
i(0) = 0.
c 1 + c 2 = q0
α c 1 + β c2 = 0

β q0

c1 =
α−β
αq0

c2 =
.
α−β
L’intensità di corrente i(t) è perciò
i(t) =
α β q0 −βt
(e
− e−αt ).
α−β
Si può osservare che, essendo
lim i(t) = 0,
t→+∞
l’intensità di corrente tende asintoticamente a 0 (vedere Figura 6).
i(t)
t
O
Figura 6: RLC con ∆ > 0
12
3.2
q
∆ < 0 =⇒ R < 2 CL
L’equazione (21) fornisce due soluzioni complesse coniugate
r
4L
i
− R2
R
C
λ1,2 = −
±
.
2L
2L
Poniamo per comodità
r
4L
− R2
C
= ω.
2L
Dunque l’integrale generale della (20) è
(22)
R
q(t) = e− 2L t (c1 cos ωt + c2 sin ωt).
L’espressione dell’intensità di corrente i(t) diventa perciò
R
dq
R −Rt
=
e 2L (c1 cos ωt + c2 sin ωt) − e− 2L t (−c1 ω sin ωt + c2 ω cos ωt).
dt
2L
(23)
Affinchè siano soddisfatte le due condizioni iniziali
i(t) = −
q(0) = q0 ,
dovrà essere
da cui
i(0) = 0,
(
q0 = c1
R
c1 − c2 ω,
0 = 2L
(24)


c = q0

 1


c2 = Rq0 .
2ωL
Sostituendo questi valori di c1 e c2 nella (23) otteniamo
R
i(t) = q0 e− 2L t sin ωt
R2 + 4L2 ω 2
.
4ωL2
(25)
Ricavando ω 2 dalla (22) e sostituendolo nel fattore R2 + 4L2 ω 2 della (25)
otteniamo infine
q0 − R t
e 2L sin ωt.
i(t) =
LCω
13
q ´
Si vede cosı̀ che, se la resistenza è sufficientemente piccola R < 2 CL , la
corrente di scarica del condensatore è una corrente alternata con intensità
decrescente in modo esponenziale (vedere Figura 7).
³
i(t)
O
t
Figura 7: RLC con ∆ < 0
q
3.3
∆ = 0 =⇒ R = 2
L
C
La carica q(t) varia nel tempo secondo la legge
R
q(t) = (c1 + c2 t) e− 2L t .
La carica sul condensatore decresce, tendendo asintoticamente a 0. L’intensità di corrente sarà perciò
µ
¶
R
R
R
dq
− c2 + c2 t e− 2L t .
i(t) = − = c1
dt
2L
2L
Tenendo conto delle condizioni iniziali
q(0) = q0 ,
abbiamo
i(0) = 0,
R2 − R t
t e 2L .
4L2
Essendo lim i(t) = 0, anche in questo caso l’intensità di corrente tende
i(t) = q0
t→+∞
asintoticamente a 0 (vedere Figura 8).
14
i(t)
O
t
Figura 8: RLC con ∆ = 0
4
Regime variabile in un circuito elettrico.
Circuito LC
Interessa particolarmente in caso in cui la resistenza sia trascurabile. In
queste condizioni la legge di Ohm generalizzata si riduce a
L
di
q
+ = 0,
dt C
cioè
d2 q
q
+
= 0.
(26)
2
dt
LC
Siamo in presenza di un’equazione differenziale del secondo ordine lineare
omogenea a coefficienti costanti, la cui equazione caratteristica
λ2 +
1
=0
LC
1
ammette le due radici immaginarie opposte λ = ±i √LC
e cioè, ponendo
1
ω = √LC ,
λ = ±iω.
Si ha cosı̀ che l’andamento della carica q(t) sulle armature del condensatore
è
q(t) = c1 cos ωt + c2 sin ωt.
(27)
15
Derivando rispetto a t la (27) si ha
i(t) = −
dq
= c1 ω sin ωt − c2 ω cos ωt.
dt
(28)
Tenendo conto delle condizioni iniziali
q(0) = q0 ,
i(0) = 0,
si ottiene, dalla (27) e dalla (28),
(
q0 = c 1
0 = −c2 ω
da cui
(
c 1 = q0
c2 = 0.
La corrente di scarica sarà perciò
i(t) = q0 ω sin ωt.
La scarica è dunque oscillatoria (vedere Figura 9), con ampiezza costante
q0 ω, ed il periodo
√
2π
= 2π LC
T =
ω
prende il nome di periodo proprio del circuito.
i(t)
O
t
Figura 9: corrente di scarica in circuito LC
16
5
Il fenomeno della risonanza.
Supponiamo di avere un circuito RLC in cui è presente anche un generatore
di corrente alternata di frequenza Ω 6= 0. L’equazione che governa il circuito
allora diventa
d2 q
dq
1
L 2 +R
+ q = V0 sin Ωt.
(29)
dt
dt C
con le condizioni iniziali q(0) = q0 e i(0) = 0. L’equazione è pertanto
contraddistinta dalla presenza del termine forzante V0 sin Ωt.
Prima di risolvere l’equazione (29), è necessario enunciare (senza dimostrazione) i seguenti risultati generali:
Teorema 1. Data un’equazione differenziale ordinaria lineare del secondo
ordine a coefficienti costanti completa
ay 00 + by 0 + cy = f (t),
il suo integrale generale è dato dalla somma dell’integrale generale yo (t)
dell’equazione omogenea associata
ay 00 + by 0 + cy = 0
e di una soluzione particolare yp (t) dell’equazione completa.
Teorema 2. Sia data un’equazione differenziale ordinaria del secondo ordine
lineare a coefficienti costanti completa
ay 00 + by 0 + cy = f (t),
con
f (t) = k sin βt,
k, β ∈ R.
Si hanno i seguenti casi:
1. se iβ non è soluzione dell’equazione caratteristica
aλ2 + bλ + c = 0
allora una soluzione particolare della (30) è del tipo
yp (t) = A sin(Ωt + α),
con A, α costanti reali da determinarsi;
17
(30)
2. se iβ è soluzione dell’equazione caratteristica, allora una soluzione particolare della (30) è del tipo
yp (t) = At sin(Ωt + α),
con A, α costanti reali da determinarsi. In quest’ultimo caso, matematicamente si dice che siamo in presenza del fenomeno della risonanza.
Vogliamo cercare di indagare e di scoprire se e in quale misura
la risonanza da un punto di vista matematico è legata al fenomeno
della risonanza in campo elettronico.
Torniamo alla (29). L’equazione caratteristica ad essa associata è
L λ2 + R λ +
1
= 0.
C
(31)
Posto
L
∆ = R2 − 4 ,
C
ci occupiamo di risolvere la (29) quando
r
L
R<2
e R 6= 0.
C
Sappiamo già che l’integrale generale dell’equazione omogenea associata alla
(29) è
R
q0 (t) = e− 2L t (c1 cos ωt + c2 sin ωt).
con c1 , c2 costanti arbitrarie e
√
ω=
−∆
.
2L
Come visto nel Teorema 2, sicuramente una soluzione particolare qp (t) della
(29) è del tipo
qp (t) = A sin(Ωt + α).
(32)
Non può essere
qp (t) = At sin(Ωt + α)
18
perchè in tal caso iΩ dovrebbe essere soluzione dell’equazione caratteristica
(31) e quindi dovremmo avere
L(iΩ)2 + RiΩ +
da cui
−LΩ2 +
1
=0
C
1
+ iRΩ = 0,
C
il che comporterebbe
−LΩ2 +
1
= 0 e R = 0,
C
contro le nostre ipotesi (R 6= 0). Troviamo allora A e α nella (32). Abbiamo
qp0 (t) = AΩ cos(Ωt + α)
e
qp00 (t) = −AΩ2 sin(Ωt + α).
Sostituendo nella (29) avremo
−LAΩ2 sin(Ωt + α) + RAΩ cos(Ωt + α) +
A
sin(Ωt + α) = V0 sin Ωt,
C
da cui, utilizzando le formule di addizione del seno e del coseno note dalla
trigonometria,
−LAΩ2 sin Ωt cos α − LAΩ2 cos Ωt sin α + RAΩ cos Ωt cos α−
A
A
− RAΩ sin Ωt sin α + sin Ωt cos α + cos Ω sin α = V0 sin Ωt.
C
C
Pertanto dovrà essere


−LAΩ2 cos α − RAΩ sin α + A cos α = V0
C
A

2
−LAΩ sin α + RAΩ cos α + sin α = 0
C
da cui
µ
¶
1

2

− LΩ sin α = −RΩ cos α

¶
µC
1

2

− LΩ A cos α − ARΩ sin α = V0

C
19
e, dividendo ambo i membri delle 2 equazioni per Ω,
µ
¶
1


− LΩ sin α = −R cos α

µ ΩC
¶
1
V0


− LΩ cos α − R sin α =

LΩ
AΩ
Poniamo
def
X = ΩL −
Allora otteniamo
Pertanto
1
.
ΩC


tan α = R
X
V

−X cos α − R sin α = 0 .
AΩ

R = X tan α
−X cos α − X tan α sin α =
da cui
V0
AΩ

R = X tan α
2
−X cos α − X sin α = V0 .
cos α
AΩ
e quindi
In definitiva troviamo

R = X tan α
1
V0
−
=
cos α
AXΩ


α = arctan R
X
V0

A = −
cos α
ΩX
Allora
V0
cos α sin(Ωt + α)
ΩX
R
con α = arctan X
. L’integrale generale della (29) pertanto è, in base al
Teorema 1,
qp (t) = −
R
q(t) = e− 2L t (c1 cos ωt + c2 sin ωt) −
20
V0
cos α sin(Ωt + α).
ΩX
(33)
Per l’intensità di corrente avremo
R
R −Rt
dq
i(t) = − =
e 2L (c1 cos ωt + c2 sin ωt) − e− 2L t (−c1 ω sin ωt + c2 ω cos ωt)+
dt
2L
V0
cos α cos(Ωt + α).
+
X
Ponendo α = ϕ + π2 , si ha
³
π´
cos α = cos ϕ +
= − sin ϕ
2
e
³
π´
cos(Ωt + α) = cos Ωt + ϕ +
= − sin(Ωt + ϕ).
2
Quindi
i(t) = −
R
R −Rt
dq
=
e 2L (c1 cos ωt + c2 sin ωt) − e− 2L t (−c1 ω sin ωt + c2 ω cos ωt)+
dt
2L
V0
+
sin ϕ sin(Ωt + ϕ).
X
, segue che
Poichè tan ϕ = − tan1 α = − X
R
sin ϕ = − cos α = − √
1
1 + tan2 α
= −√
X
.
R2 + X 2
Cosı̀ abbiamo in definitiva che
R
R −Rt
i(t) =
e 2L (c1 cos ωt + c2 sin ωt) − e− 2L t (−c1 ω sin ωt + c2 ω cos ωt)−
2L
V0
sin(Ωt + ϕ).
−√
2
R + X2
(34)
def √ 2
Le quantità X e Z = R + X 2 sono rispettivamente chiamate reattanza e
impedenza del circuito. Imponiamo ora le condizioni iniziali per trovare le
costanti arbitrarie c1 e c2 .
Imponendo q(0) = q0 nella (33) otteniamo
c 1 = q0 +
V0 cos α sin α
V0 sin ϕ cos ϕ
= q0 −
.
ΩX
ΩX
Imponendo i(0) = 0 nella (34) otteniamo
c2 =
Rq0
RV0 sin ϕ cos ϕ
V0 sin ϕ
.
−
− √
2Lω
2LωΩX
ω R2 + X 2
21
A noi interessa ragionare per un tempo t sufficientemente grande, cioè ci
interessa studiare il fenomeno una volta superato il transitorio. Poichè
·
¸
R
R −Rt
−
t
lim
e 2L (c1 cos ωt + c2 sin ωt) − e 2L (−c1 ω sin ωt + c2 ω cos ωt) = 0
t→+∞ 2L
possiamo dire che, superato il transitorio, l’intensità di corrente sarà
i(t) = − √
V0
sin(Ωt + ϕ).
+ X2
(35)
R2
Consideriamo (in modulo) la sua ampiezza, come funzione di Ω:
A(Ω) = √
V0
=s
+ X2
R2
µ
V0
1
R2 + ΩL −
ΩC
¶2 .
Proviamo a vedere per quali valori della frequenza esterna Ω si ha che A(Ω)
è massima:
¢¡ 1
¢
¡
− ΩL
V0 L + Ω21C ΩC
dA
= h
.
¡
¢ i3
dΩ
1 2 2
2
R + ΩL − ΩC
Si ha che
quando
dA
≥0
dΩ
1
− ΩL ≥ 0,
ΩC
cioè quando
1 − Ω2 LC ≥ 0.
Otteniamo allora che A(Ω) è massima quando
Ω= √
e vale
1
LC
V0
.
R
1
si chiama frequenza di risonanza del circuito. Si
La frequenza Ω = √LC
ha quindi risonanza quando la frequenza esterna coincide con la frequenza
che ci dà la massima oscillazione dell’intensità di corrente del circuito.
Amax =
22
Notiamo che, in condizioni di risonanza, lo sfasamento ϕ tra l’intensità
di corrente i(t) e la tensione esterna applicata V0 sin(Ωt), pari a
µ
¶
µ
1 ¶
ΩL − ΩC
X
ϕ(Ω) = arctan −
= arctan −
R
R
si annulla.
In condizioni di risonanza, dunque, l’intensità di corrente diventa, dopo
opportune semplificazioni e ricordando che ϕ = 0,
µ
µ
¶
¶
R
R −Rt
Rq0
Rq0
t
−
i(t) =
e 2L q0 cos ωt +
sin ωt − e 2L −q0 ω sin ωt +
cos ωt −
2L
2Lω
2L
V0
sin Ωt =
−
R µ
¶
R
R2 q0
V0
− 2L
t
=e
+ q0 ω sin ωt −
sin Ωt.
2
4L ω
R
In particolare, superato il transitorio, l’intensità di corrente diventa
i(t) = −
V0
sin Ωt.
R
1
Osservazione. Notiamo che, in condizioni di risonanza (Ω = √LC
), superato
il transitorio, quando R → 0 (cioè quando la resistenza all’interno del circuito diventa trascurabile), le oscillazioni dell’intensità di corrente crescono
all’infinito (in modulo):
V0
lim+
= +∞.
R→0 R
Possiamo in qualche modo trovare un riscontro matematico a questo fenomeno?
Per rispondere a quest’ultima domanda, consideriamo il circuito ideale
LC, in cui R = 0, con generatore di tensione sinusoidale esterno:
Lq 00 +
1
q = V0 sin Ωt,
C
(36)
con le condizioni iniziali q(0) = q0 e i(0) = 0. Supponiamo di metterci in
1
. Notiamo che in queste condizioni, vi
condizioni di risonanza, cioè Ω = √LC
1
è anche risonanza da un punto di vista matematico perchè se Ω = √LC
allora
iΩ è soluzione dell’equazione caratteristica:
Lλ2 +
1
= 0.
C
23
1
Come vediamo, Ω = √LC
è esattamente la frequenza propria del circuito e
coincide con la frequenza di risonanza che si verifica quando R 6= 0.
Nel caso di risonanza, inoltre, si ha in questo caso che
q
√
4 CL − R2
1
−∆
ω=
=
=√
= Ω.
2L
2L
LC
Risolviamo la (36). Sappiamo che l’integrale generale dell’equazione omogenea associata è
q0 (t) = c1 cos ωt + c2 sin ωt
con c1 , c2 costanti arbitrarie. Una soluzione particolare della (36) è
qp (t) = At sin(ωt + α)
che scriviamo nella forma equivalente
qp (t) = t(A cos ωt + B sin ωt),
con A, B costanti da determinarsi. Abbiamo
qp0 (t) = A cos ωt + B sin ωt + t(−Aω sin ωt + Bω cos ωt)
e
qp00 (t) = −2Aω sin ωt + 2Bω cos ωt + t(−Aω 2 cos ωt − Bω 2 sin ωt).
Sostituiamo nella (36) e semplifichiamo:
µ
¶
A
−2ALω sin ωt + 2BLω cos ωt + −ALω +
t cos ωt+
C
µ
¶
B
2
−BLω +
t sin ωt = V0 sin ωt.
C
2
Essendo ω 2 =
1
,
LC
avremo
−ALω 2 +
1
A
A
= −AL
+ =0
C
LC C
−BLω 2 +
1
B
B
= −BL
+ = 0.
C
LC C
e
24
Allora si ha
−2ALω sin ωt + 2BLω cos ωt = V0 sin ωt.
Pertanto dovrà essere
da cui
(
−2ALω = V0
2BLω = 0


A=−
B = 0.
V0
2Lω
Una soluzione particolare della (36) è quindi
qp (t) = −
V0
t cos ωt.
2Lω
Otteniamo cosı̀ che l’integrale generale della (36) è
q(t) = c1 cos ωt + c2 sin ωt −
V0
t cos ωt.
2Lω
Allora l’intensità di corrente è
i(t) = −
dq
V0
V0
= c1 ω sin ωt − c2 ω cos ωt +
cos ωt −
t sin ωt.
dt
2Lω
2L
Imponendo le condizioni iniziali troviamo

 c 1 = q0
V0
 c2 =
.
2Lω 2
Pertanto, dopo opportune semplificazioni, l’intensità di corrente del circuito
LC con generatore di tensione sinusoidale esterno è
µ
¶
V0
i(t) = q0 ω −
t sin ωt.
(37)
2L
Notiamo che in questo caso l’ampiezza dell’oscillazione dell’intensità di corrente è funzione del tempo:
A(t) = q0 ω −
25
V0
t.
2L
Essa, per t → +∞, tende all’infinito (in modulo), in perfetto accordo con
quanto studiato nel caso della risonanza del circuito RLC quando R → 0.
Otteniamo cioè il classico fenomeno della risonanza in cui l’ampiezza delle
oscillazioni diventa sempre più grande per tendere all’infinito.
Osserviamo inoltre che, superato il transitorio τ = 2L
, si ha che
R
|A(τ )| ∼
V0 2L
V0
·
=
2L R
R
avendo trascurato il termine q0 ω che per tempi sufficientemente grandi non
è influente. Vediamo cosı̀ che A(τ ) è esattamente l’ampiezza massima di
oscillazione dell’intensità di corrente che si aveva nel caso in cui R 6= 0, in
condizioni di risonanza.
26