Spettroscopia rotazionale
•
•
La spettroscopia rotazionale si occupa dello studio delle eccitazioni rotazionali delle molecole.
La spettroscopia rotazionale è utile in fase gas, in cui le molecole sono libere di ruotare e le rotazioni
sono quantizzate. In fase liquida o solida le rotazioni sono inibite.
•
Può essere effettuata in emissione o assorbimento nell’intervallo spettrale delle onde radio, delle
microonde e della radiazione infrarossa
Per poter osservare uno spettro rotazionale occorre che la molecola sia dotata di momento di dipolo
permanente. È il momento di dipolo della molecola che fa sì che il campo elettrico dell’onda
elettromagnetica eserciti un momento (di una forza) sulla molecola, facendola ruotare più
velocemente (in eccitazione - assorbimento) o lentamente (in diseccitazione - emissione).
Le molecole biatomiche simmetriche come O2 o H2 non posseggono momento di dipolo permanente
e non mostrano spettro rotazionale (se non in presenza di concomitante eccitazione elettronica)
•
•
•
Può esser effettuata con sorgenti luminose di opportuna intensità (Laser) per effetto Raman
•
La spettroscopia rotazionale permette di risalire al momento di inerzia di una molecola e da qui alle
distanze di legame tra gli atomi presenti.
Il momento di inerzia di una molecola rispetto ad un asse qualsiasi passante per il suo centro di
massa è dato da
dove ri è la distanza dall’asse.
I = mi ri 2
•
•
i
Ciascun sistema è dotato di tre assi principali di inerzia mutualmente perpendicolari: si definiscono
tre momenti principali di inerzia Ia Ib Ic.
Molecola lineare Ia = Ib
Ic=0.
Rotore simmetrico Ia = Ib > Ic oppure Ia > Ib = Ic .
Rotore sferico Ia = Ib = Ic.
Rotore asimmetrico Ia
Ib
Ic.
1
Spettroscopia rotazionale – assorbimento/emissione
Rotori lineari: molecole biatomiche e poliatomiche
•
La probabilità di transizione tra due stati rotazionali è proporzionale al quadrato del momento di
transizione R = Ψ* µΨ dτ
if
rf
ri
•
Le regole di selezione rotazionale stabiliscono le condizioni affinché l’intensità di una transizione
non sia nulla
1.
2.
3.
La molecola deve possedere momento di dipolo permanente diverso da zero
∆J = ± 1
∆MJ = 0, ± 1 (solo se la molecola è in campo elettrico o magnetico)
h2
J ( J + 1) , I = µ R 2 , µ =
m1m2
m1 + m2
•
Si è visto in precedenza che per un rotore rigido Er =
•
La stessa espressione si ottene per qualsiasi molecola lineare; poiché I è maggiore, i livelli
energetici saranno tra loro più vicini.
Er
h
In pratica si misurano frequenze (ν ) e non energie
stati (o termini) F ( J ) = h = 2 J ( J + 1) = BJ ( J + 1)
8π I
•
•
•
8π 2 I
E
h
Oppure numeri d’onda ( w = 1 λ )
stati (o termini) F ( J ) = r = 2 J ( J + 1) = BJ ( J + 1)
hc 8π cI
Da cui ν = w f − wi (o ν ) = F ( J + 1) − F ( J ) = 2 B ( J + 1)
2
Spettroscopia rotazionale – assorbimento/emissione
3
Spettroscopia RAMAN rotazionale
•
•
•
•
•
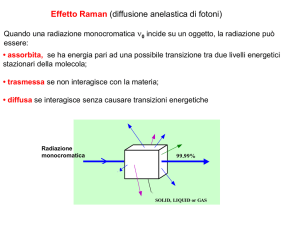
La spettroscopia RAMAN è usata per studiare transizioni rotazionali, vibrazionali, elettroniche.
L’effetto RAMAN è poco intenso: necessita di sorgenti ad alta intensità
Laser
La grandezza fisica che determina il grado di diffusione della radiazione incidente è la polarizzabilità.
La polarizzabilità è una grandezza tensoriale: può dipendere dalla direzione lungo cui la si osserva
Quando radiazione monocromatica incide su un campione se non è assorbita, il campo elettrico
oscillante induce nella molecola un dipolo elettrico legato alla polarizzabilità
α xx α xy α xz
α = α yx α yy α yz
α zx α zy
•
•
•
•
µ = α E;
E = E = E0 sin(ωt ) = E0 sin(2π cν t )
α zz
Se la molecola ruota con frequenza ν rot l’ampiezza della polarizzabilità varierà anche essa.
La radiazione ‘vedrà’ la polarizzabilità variare a una frequenza doppia rispetto alla frequenza di
rotazione (l’ellissoide di polarizzabilità è simmetrico per rotazioni di π).
La variazione di polarizzabilità con la rotazione è data da α = α 0,r + α1,r sin 2π c(2ν rot )t con α 0,r pol.media, α1,r amp.variaz.
Si ricava dunque per il modulo del dipolo indotto
1
2
1
2
µ = α 0,r E0 sin(2π cν t ) − α1,r E0 cos 2π c(ν + 2ν rot )t + α1,r E0 cos 2π c(ν − 2ν rot )t
•
•
Tutti e tre i termini rappresentano scattering di radiazione: il primo termine rappresenta la diffusione
della radiazione alla stessa lunghezza d’onda (scattering Rayleigh). Il secondo e terzo termine
rappresentano i termini di scattering Raman, rispettivamente detti di anti-Stokes e Stokes.
Poiché in un sistema quanto-meccanico la frequenza di rotazione può assumere solo valori discreti,
così i termini di Stokes e anti-Stokes daranno luogo a righe discrete.
4
Spettroscopia RAMAN rotazionale
Rotori lineari: molecole biatomiche e poliatomiche
•
Lo scattering Raman obbedisce alle seguenti regole di selezione
1.
2.
•
∆J = 0, ± 2 (J=0 corrisponde allo scattering Rayleigh)
La molecola deve possedere α anisotropa: ciò esclude solo i rotori sferici ma non le molecole lineari
simmetriche (che non hanno un momento di dipolo permanente)
Da quanto visto in precedenza ∆ν = ν − ν Laser = F ( J + 2) − F ( J ) = 4 BJ + 6 B con ∆ν positivo per
anti-Stokes e negativo per Stokes
5
Spettroscopia vibrazionale
•
•
La spettroscopia vibrazionale si occupa dello studio delle eccitazioni vibrazionali delle molecole.
La spettroscopia vibrazionale è utile in fase gas, liquida o solida.
•
•
Può essere effettuata in emissione o assorbimento nell’intervallo spettrale della radiazione infrarossa
Può essere effettuata con sorgenti luminose di opportuna intensità (Laser) per effetto Raman
•
La spettroscopia vibrazionale permette di risalire alla forza elastica che caratterizza un legame tra
atomi di una molecola. Questa dipende da un sottile bilanciamento tra repulsione tra nuclei,
repulsione tra elettroni e attrazione tra nuclei ed elettroni. Queste interazioni non sono influenzate
dalla massa nucleare: la costante elastica non è influenzata dalla sostiuzione isotopica.
Come per la spettroscopia rotazionale, anche per la spettroscopia vibrazionale è conveniente usare
anziché i livelli energetici i seguenti termini, espressi in numeri d’onda (vibrazionali).
•
Evibr = hcν vibr v +
1
, ν = cν vibr
2
Evibr
1
= G (v) = ν vibr v +
hc
2
6
Spettroscopia vibrazionale infrarossa - teoria
•
•
•
•
*
Il momento di transizione tra due stati i e f è dato da Rif = Ψ vf µΨ vi dx
La variabile x indica lo spostamento (x = r-re) della distanza internucleare rispetto all’equilibrio.
Il momento di dipolo =0 per una molecola biatomica omonucleare
Rif=0 e tutte le transizioni
vibrazionali sono proibite.
Per una molecola biatomica eteronuclare 0 e varia con x. Questa variazione può essere espressa
in serie di Taylor intorno alla posizione di equilibrio.
2
µ = µe +
•
•
x+
e
*
Ne consegue che il momento di transizione Rif = µe Ψ vf Ψ vi dx +
1 d µ
2! dx 2
dµ
dx
e
x 2 + ...
e
Ψ*vf xΨ vi dx + ...
Per la proprietà delle autofunzioni dell’hamiltoniana di essere ortogonali tra loro si ha che il primo
integrale si annulla. Si ha dunque
Rif =
•
•
dµ
dx
dµ
dx
e
Ψ*vf xΨ vi dx + ...
Il primo termine nella somma è diverso da zero se ∆v = ±1
Regola di selezione vibrazionale
Se lo spettro è osservato in assorbimento e a temperature ordinarie, le intensità sono regolate anche
dalla popolazione dei livelli di partenza i: questa decresce rapidamente all’aumentare del livello.
Nv
E
= exp − v
N0
K BT
•
•
Ogni transizione vibrazionale è chiamata banda, eventualmente suddivisa in una struttura fine dovuta
2
dµ
alle concomitanti transizioni rotazionali (solo in fase gas).
2
dx e . Può verificarsi che una
Le intensità delle transizioni sono proporzionali a Rif e dunque a
transizione permessa sia in realtà a intensità nulla se la derivata è uguale a 0!
7
Spettroscopia vibrazionale RAMAN - teoria
•
•
•
Sia per molecole omonucelari e eteronucleari (biatomiche) la polarizzabilità varia durante il moto di
vibrazione, portando all’effetto Raman vibrazionale.
Questa variazione può essere visualizzata pensando all’ellissoide di polarizzabilità che si espande e
si contrae alla frequenza (o meglio numero d’onda ν vibr ) della vibrazione.
Ne consegue che cambia nel tempo il modulo del momento di dipolo indotto dalla radiazione
monocromatica incidente di numero d’onda ν
1
2
1
2
µ = α 0,vibr E0 sin(2π cν t ) − α1,vibr E0 cos 2π c(ν + ν vibr )t + α1,vibr E0 cos 2π c(ν − ν vibr )t
•
•
L’espressione è simile a quanto visto nella Raman rotazionale, ad eccezione che la frequanza di
variabilità della polarizzabilità è pari (e non il doppio) della frequenza della vibrazione.
La variazione della polarizzabilità può essere espansa in serie di Taylor e ottenere Regola di selezione
α = αe +
•
•
•
con α 0,vibr pol.media durante la vibraz., α1,vibr amp.variaz.
dα
dx
x+
e
1 d 2α
2! dx 2
x 2 + ...
e
Rif =
dα
dx
e
E0 Ψ*vf xΨ vi dx + ...
∆v = ±1
Il vantaggio della spettroscopia Raman è che sono ammesse transizioni anche in molecole
biatomiche omonucleari!
Le intensità delle transizioni dipendono dalle popolazioni iniziali dei livelli e dunque da T.
2
2
Le intensità delle transizioni sono proporzionali a Rif e dunque a dα . Per meglio visualizzare il
dx e
problema è utile introdurre la polarizzabilità media
α = 13 (α xx + α yy + α zz )
Rispetto a d /dx, d /dx varia poco con
r
le intensità delle transizioni
Raman sono meno sensibili al
contorno della molecola (come il
solvente)
8
Spettroscopia vibrazionale – effetti anarmonici
•
Anarmonicità elettronica: dovuto ai termini di ordine superiore
omessi negli sviluppi di
e
modifica delle regole di
selezione sia nella Raman che nella spettroscopia infrarossa a
∆v = ±1, ±2, ±3,...
•
Le intensità dovute ai termini di ordine superiore (overtones)
sono però deboli
•
Anarmonicità meccanica: dovuta alla forma non parabolica del
potenziale di interazione tra i nuclei
–
•
•
•
•
Allontanando i nuclei progressivamente la molecola a un certo
punto dissocia! De è l’energia di dissociazione
L’anarmonicità meccanica è più importante di quella elettronica
Anche per l’anarmonicità meccanica si ha una modifica delle
regole di selezione (sia Raman che infrarossa)
G (v ) = ν vibr v +
∆v = ±1, ±2, ±3,...
Le transizioni di overtone sono solitamente deboli
L’anarmonicità meccanica modifica i termini vibrazionali:
–
–
I termini si avvicinano tra loro
I termini convergono verso il limite di dissociazione
G (v) = ν vibr ,e v +
1
1
− ν vibr ,e xe v +
2
2
num.d’onda di
vibrazione di un
oscillatore
armonico classico
per spostamenti
infinitesimi rispetto
a re
1
2
2
+ ν vibr ,e ye v +
costanti di
anarmonicità
9
1
2
3
+ ...
Spettroscopia vibrazionale – molecole poliatomiche
•
•
•
•
•
•
•
In una molecola poliatomica ogni nucleo interagisce con gli altri
lo spostamento di un nucleo dal
suo centro comporta la oscillazione di tutto il sistema.
Da un punto di vista classico si può pensare che le varie masse siano tra loro legare da interazioni di
tipo elastico
Modo normale di vibrazione si ha quando tutti i nuclei si muovono di
moto armonico, con la stessa fase e frequenza anche se in generale
con differenti ampiezze
I modi normali possono essere di differente natura coinvolgendo stiramenti, compressioni,
piegamenti dei legami tra gli atomi
Ogni modo normale (i) è caratterizzato da una propria frequenza caratteristica e le transizioni
1
vibrazionali che coinvolgono tale modo sono quantizzate G (v ) = ν
i
vibr ,i vi +
2
possono essere usate per riconoscimento molecolare
Anche se in generale un modo normale di vibrazione implica il moto di tutti gli atomi nella molecola,
in molti casi il movimento è ragionevolmente localizzato in una sola parte della molecola.
Per la vibrazione che coinvolge solo un gruppo di atomi all’interno della molecola si parla di numero
d’onda di vibrazione di gruppo
riconoscimento molecolare (Tavole di correlazione)
10
Spettroscopia IR vibrazionale – Strumentazione
Preparazione campioni
•
No acqua!
•
Campione tra dischi di sale o mescolato a
KBr
•
La maggior parte dei moderni spettrometri basano il loro funzionamento su metodi interferenziali e
sulla trasformata di Fourier
per maggiori dettagli si veda M. Hollas, Modern Spectroscopy, Wiley
11
Spettroscopia IR vibrazionale – alcuni esempi
12