18 Problemi proposti con risposte
Cap. 1 – Vettori
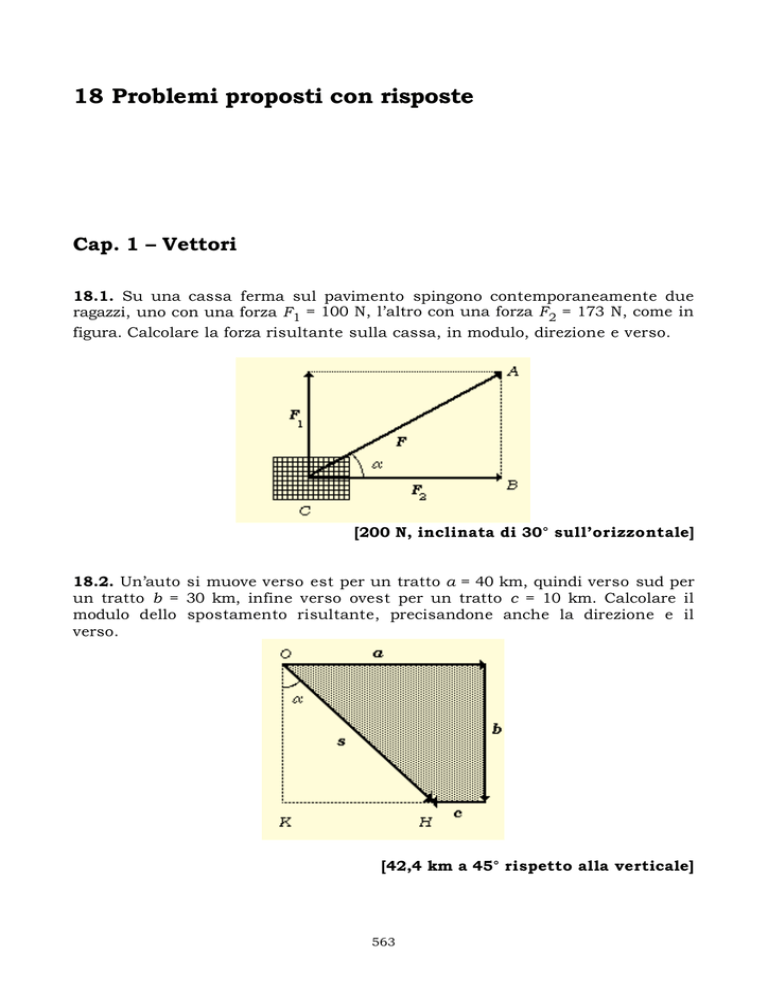
18.1. Su una cassa ferma sul pavimento spingono contemporaneamente due
ragazzi, uno con una forza F1 = 100 N, l’altro con una forza F2 = 173 N, come in
figura. Calcolare la forza risultante sulla cassa, in modulo, direzione e verso.
[200 N, inclinata di 30° sull’orizzontale]
18.2. Un’auto si muove verso est per un tratto a = 40 km, quindi verso sud per
un tratto b = 30 km, infine verso ovest per un tratto c = 10 km. Calcolare il
modulo dello spostamento risultante, precisandone anche la direzione e il
verso.
[42,4 km a 45° rispetto alla verticale]
563
18.3. Dati i due vettori a = 2 (i + 3 j) m e b = 2 ( 3 i + j) m, calcolare: a) il
prodotto scalare, b) il prodotto vettoriale.
[13,84 m2; 8 m2, entrante nel piano della pagina]
18.4. Dati i due vettori perpendicolari a = (3,1,–4) m e b = (x, 2, 1) m, calcolare:
a) x e b) il modulo del loro prodotto vettoriale.
[0,67 m; 11,9 m2]
18.5. Il vettore a = (1,2,3) m è perpendicolare al vettore b = (–1,1, bz) m.
Calcolare bz.
[–0,33 cm]
18.6. Dati i due vettori a = 3 i + 2 j – 2 k e b = 2 i – 2 j + k, determinare: a)
l’angolo tra i due vettori, b) il prodotto vettoriale, c) il vettore b – a; d) il vettore
(b – a) (b + a).
[90°; –2 i + 7 j – 10 k; –i – 4 j + 3 k; 4 i + 14 j + 20 k]
18.7. Calcolare l’angolo tra i vettori a = 3 i – j + 2 k e b = – i + 3 j – 4 k.
[137°12’]
18.8. Calcolare:
i k, k k, i j k, k j , i j k.
[– j; 1; 1; – i; 1]
564
18.9. Dati vettori a e 3 a, calcolarne: a) il prodotto vettoriale, b) il modulo della
differenza, c) il prodotto scalare, d) il prodotto scalare della somma per la
differenza.
[0; 2 a; 3 a2; – 8 a2]
18.10. Calcolare l’angolo tra i vettori a = 2 i – 3 j e b = 2 j + k.
[138°5’]
18.11. Dati i vettori
calcolare:
a = 2 i – j + 3 k,
b = – i +2 j + k,
( a b) a
( a b) b
( b a) i
( a b) a
( b a) b.
[0, 0, 7, – 12 i + 27 j + 17 k, 11 i – 4 j + 19 k]
Cap. 2 – Cinematica
18.12. Se un mobile inizialmente fermo nell’origine dell’asse x si muove lungo
tale asse con accelerazione a = k t, essendo k una costante, ricavare la legge
oraria del moto e le dimensioni di k.
[k t3/6; [k]= [a] [t–1] =[L T–3]]
18.13. Un punto materiale passa in 10 s da velocità v = (i + 3 j + 5 k) m/s a
velocità u = (2 i + 4 j + 6 k) m/s. Calcolare: a) l’aumento del modulo della
velocità, b) l’aumento di velocità, c) l’accelerazione vettoriale media, d) il
modulo dell’aumento di velocità.
[1,56 m/s; 1,73 m/s; 0,17 m/s 2; 1,73 m/s]
18.14. Due sassi vengono lanciati dal suolo con la stessa velocità iniziale v =
200 m/s e lo stesso angolo di alzo = 45° con un ritardo to = 5 s uno dall’altro.
Calcolare: a) dopo quanto tempo dal lancio del primo si incontreranno, b) a
quale distanza dal punto di lancio, c) a quale quota.
[16,9 s; 2,39 km; 990,5 m]
565
18.15. Un punto materiale inizialmente sull’asse x in xo si muove con legge v =
k/x. Ricavare le leggi orarie di x, v e a in funzione di k e di xo.
[x =
x02 + 2k t ; v =
k
x02 + 2k t
;a =
dv
k2
= 2
]
dt
(x + 2k t)3/2
0
18.16. Un’auto viaggia su strada orizzontale rettilinea con velocità v1= 30 m/s
quando viene frenata uniformemente in t = 8 s fino all’arresto. Calcolare: a) la
decelerazione dell’auto, b) la distanza di arresto, c) la velocità dopo 2 s
dall’inizio della frenata, d) la distanza percorsa dopo 2 s dall’inizio della
frenata.
[3,75 m/s 2; 120 m; 22,5 m/s; 52,5 m]
18.17. Due oggetti cadono contemporaneamente dall’altezza h = 1 m, il primo
in caduta libera, il secondo lungo un piano liscio inclinato di 45°. Calcolare: a)
il tempo di caduta del primo, b) quello del secondo, c) le due velocità finali, d)
dove si trova il secondo oggetto quando il primo è arrivato a terra.
[0,45 s; 0,64 s; 4,43 m/s; avrà percorso 0,7 m lungo il piano]
18.18. Un punto materiale si muove lungo l’asse x con legge
v=
6x ,
espressa in unità SI. Ricavare: a) la legge oraria del moto e b) le costanti del
moto.
[È un moto uniformemente accelerato con a = 3 m/s2; x o = 0; v o = 0]
18.19. Un proiettile viene lanciato dal livello del suolo con angolo di alzo =
60° e velocità iniziale vo = 80 m/s. Calcolare: a) la gittata, b) la velocità al
culmine, c) il tempo di volo, d) la massima quota raggiunta.
[565,6 m; 40 m/s; 14,1 s; 244,9 m]
18.20. Un proiettile viene lanciato dal suolo con velocità iniziale vo = 60 m/s in
modo che la gittata sia pari alla metà dell’altezza massima. Calcolare il tempo
di volo.
[12,1 s]
18.21. Due oggetti vengono lanciati da terra con la stessa velocità iniziale vo,
uno con angolo di alzo = 20°, l’altro con angolo di alzo = 70°. Calcolare i
rapporti tra: a) le gittate, b) i tempi di volo, c) le quote massime raggiunte.
[1; 0,36; 0,13]
566
18.22. Le equazioni parametriche del moto di un punto sono
x = 2 m, y = 2 t
2
m, z = t
2
m.
Calcolare, all’istante t = 1 s, a) la velocità del punto, b) la sua accelerazione.
[4,48 m/s; 4,48 m/s 2]
18.23. Per quale angolo di alzo la quota massima di un proiettile coincide con
la gittata, se il lancio avviene a livello del suolo?
[75°58’]
18.24. Un punto materiale descrive una circonferenza di raggio r = 2 m con
legge oraria
= 5 t rad
(unità SI).
All’istante t = 5 s, calcolare: a) la velocità periferica, b) l’accelerazione angolare,
c) l’accelerazione totale.
[10 m/s; 0; 50 m/s 2 ]
Cap. 3 – Dinamica del punto
18.25. Se due pesi identici P = 10 N sono fissati a un dinamometro come in
figura, quanto si legge sulla scala dello strumento?
[20 N]
18.26. Una massa m = 200 g appoggiata su un tavolo liscio è collegata mediante
un filo ideale che passa attraverso un foro praticato nel centro del tavolo a una
massa M e il tutto è in equilibrio mentre m sta ruotando con velocità angolare = 5 rad/s su una circonferenza di raggio r = 40 cm.
Calcolare il valore di M.
567
[204 g]
18.27. Una lastra di vetro di massa m = 2 kg si spezza sotto l’azione delle
vibrazioni infrasonore di frequenza = 10 Hz originate da una lontana
esplosione. Calcolare di quanto si flette tale lastra quando applichiamo nel suo
centro una forza F = 30 N.
[3,8 mm]
18.28. Una slitta di massa m = 15 kg viene trascinata sulla neve a velocità
costante da un cane che le applica una forza F =12 N inclinata di un angolo di
30° rispetto all’orizzontale.
Calcolare il coefficiente di attrito tra la slitta e la neve.
[0,07]
18.29. Un carico viene appeso a una fune ideale di lunghezza l e posto in
oscillazione come pendolo semplice; trascurando ogni attrito, se la fune viene
sollevata di un tratto x pari al 20% della lunghezza iniziale, di quanto varierà
percentualmente il periodo di oscillazione?
[–10,6 %]
18.30. Due forze con lo stesso modulo 2 N formano un angolo di 120°. Quale
sarà il modulo del loro risultante?
[2 N]
568
18.31. Se un corpo ha il peso di 1 dyn al polo Nord, a) quanto vale la sua
massa al polo Nord? b) e quanto all’equatore?
[1,02 mg dovunque]
18.32. Se la frequenza di un sistema massa-molla è = 5 Hz, quale sarà
l’accelerazione della massa quando lo spostamento dalla posizione di equilibrio
è s = 15 cm?
[–148 m/s 2]
18.33. Una sferetta di massa m = 50 g inizialmente in quiete nell’origine
dell’asse x si muove orizzontalmente con velocità vo = 40 m/s in un mezzo che
offre una resistenza del tipo F = – k v2, con k = 0,02 unità SI. Calcolare, dopo 20
s dall’inizio del moto: a) la velocità e b) la distanza percorsa dalla sferetta.
[12,5 cm/s; 14,4 m]
18.34. Qual è la lunghezza del filo di un pendolo semplice che batte il
secondo?
[0,993 m]
Cap. 4 – Lavoro ed Energia
18.35. Una massa puntiforme m in moto lungo l’asse x è soggetta a
un’accelerazione costante a per un tratto di lunghezza x, quindi viene
decelerata con decelerazione costante b in modo da fermarsi a una distanza l
dall’origine O. Se la massa è inizialmente in quiete nell’origine, ricavare: a)
l’espressione di x, b) l’espressione dell’energia cinetica nel punto A.
[x = b l/ (a + b); K = m a b l /(a + b)]
18.36. Un bambino seduto su un’altalena di lunghezza l = 1 m ha in mano un
pallone. L’altalena, sospesa nel punto O a distanza s = 1,3 dal suolo, viene
fatta oscillare partendo da ferma nella posizione angolare = 60°, ma giunta
nella posizione angolare = 30° al bambino sfugge di mano il pallone. Calcolare
a quale distanza d dal punto H toccherà terra il pallone.
569
[1,47 m]
18.37. Un blocco di massa m si muove lungo l’asse x in assenza di attriti sotto
l’azione di una forza F cui corrisponde un’energia potenziale
U(x) = (1 + a x + b x3) J.
Nell’origine F = 1 N e x = 1 m è una posizione di equilibrio; inoltre, il blocco è
in quiete per x = 2 m e passa dall’origine con velocità v = 3 m/s.
Determinare: a) le costanti a e b; b) la massa m; c) se la posizione di equilibrio
del blocco è stabile, instabile o indifferente.
[a = – 1 N, b = 0,33 N/m2; m = 148 g; instabile]
18.38. Una forza agisce su un punto materiale
radiale verso l’esterno con modulo F = (2/r) N,
posizione del punto P. a) Stabilire se tale forza
lavoro che essa compie per spostare il punto
posizione B (2,2) m.
P nel piano (x, y) in direzione
dove r è il modulo del vettore
è conservativa e b) calcolare il
dalla posizione A (1,1) m alla
[sì, 2,77 J]
18.39. Un palo di massa m = 100 kg viene interrato perpendicolarmente da un
blocco di massa M = 1000 kg che, dopo un salto h = 5 m, lo affonda di un tratto
s = 5 cm. Calcolare la forza resistente media offerta dal terreno.
[969,2 kN]
570
18.40. Un oggetto di massa m = 80 g viene lanciato con velocità iniziale vo= 6
m/s su un piano orizzontale scabro di coefficiente di attrito μ = 0,2. Calcolare:
a) il tempo di arresto, b) la distanza di arresto, c) dopo quanto tempo la velocità
iniziale si dimezza, d) la velocità media durante il moto.
[3,1 s; 9,2 m; 1,5 s; 3 m/s]
18.41. Un corpo in quiete viene messo in moto da una forza F = 200 N che gli
imprime in t = 10 s una velocità v = 30 m/s nella stessa direzione della forza.
Calcolare: a) l’accelerazione impressa, b) la massa del corpo, c) la potenza
impiegata.
[3 m/s 2, 66,7 kg, 6 kW]
18.42. Un uomo solleva un corpo di massa m fino a quota h. Stabilire il segno
del lavoro compiuto dall’uomo e dalla Terra e ricavare l’espressione del lavoro
compiuto dall’uomo se il sollevamento avviene con accelerazione costante 2 g.
[L uomo > 0, Lterra < 0, 3 m g h]
18.43. Se E è l’energia meccanica totale di un oscillatore armonico, quale
frazione di E sarà l’energia cinetica dell’oscillatore nella posizione x = A/2, con
A ampiezza di oscillazione ?
[3/4]
18.44. Una molla ideale di rigidità k = 10 N/m è in quiete su un piano
orizzontale liscio recando fissata a un estremo una massa m = 10 kg; se la si
allunga di s = 10 cm e poi la si rilascia, calcolare: a) l’energia totale del
sistema, b) dopo quanto tempo la massa ripassa dalla posizione iniziale, c) la
frequenza di oscillazione del sistema, d) l’accelerazione con cui m ripassa dalla
posizione iniziale di quiete.
[50 mJ; 1,57 s. 0,16 Hz; 0]
18.45. Su un blocco di massa m = 6 kg appoggiato su un piano inclinato di
altezza h = 1 m e angolo di inclinazione = 30° agiscono, oltre all’attrito (μ =
0,3), due forze F 1 = 4 N ed F 2 = 3 N come in figura. Calcolare il lavoro compiuto
sul corpo per fargli percorrere l’intero piano.
[36 J]
571
Cap. 5 – Urti. Quantità di moto. Centro di massa
18.46. Una bilia di massa m1 = 40 g è fissata su un piano liscio a una molla
ideale inizialmente scarica di rigidità k = 104 N/m. Se contro la prima bilia ne
viene lanciata frontalmente una seconda di massa m2 = 80 g con velocità v2 = 30
m/s, calcolare: a) la massima compressione della molla, b) la velocità della
bilia 2 immediatamente dopo l’urto supposto perfettamente elastico.
[8 cm; 10 m/s]
18.47. Una molla ideale di rigidità k = 1600 N/m è fissata a un blocco di massa
m1 = 40 g tenuto in quiete da un fermo che comprime la molla di un tratto d = 4
cm. A distanza d da m1 è fermo un secondo blocco di massa m2 = 20 g. Togliendo
il fermo, il blocco 1 va a urtare il blocco 2 in modo perfettamente elastico.
Calcolare: a) la velocità del blocco1 dopo l’urto, b) la massima compressione
della molla dopo il rinculo del blocco 1, c) la distanza dall’origine O a cui si
arresta il blocco 2 se la parte di piano sulla destra ha un coefficiente di attrito
μ = 0,4.
[– 2,67 m/s; 1,34 cm; 14,5 m]
18.48. Un cuneo scabro di massa M = 1 kg, inclinazione = 30° e lunghezza del
piano inclinato s = 60 cm con coefficiente di attrito μ 1 = 0,2 è in quiete su un
piano orizzontale scabro di coefficiente di attrito μ 2 = 0,1. Se dal vertice viene
lasciato libero un blocco di massa m = 100 g, calcolare: a) la velocità del cuneo
nell’istante in cui il blocco lo abbandona, b) la distanza che il cuneo percorre
sul piano orizzontale prima di arrestarsi.
[16,4 cm/s verso sinistra; 1,37 cm]
572
18.49. Un uomo R di massa m = 80 kg è in quiete all’estremità di un carrello di
massa M = 200 kg in quiete sull’asse x. Trascurando qualsiasi attrito, se l’uomo
comincia a muoversi con velocità costante v = 2 m/s relativa al carrello,
calcolare: a) la velocità acquistata dal carrello rispetto a un osservatore
assoluto A fermo nell’origine degli assi, b) la velocità assoluta dell’uomo R.
[a) 57 cm/s; b) –1,43 m/s]
18.50. Una barca di lunghezza l = 6 m e massa M = 320 kg è in quiete in acqua
ferma con un uomo di massa m = 80 kg fermo a poppa. Se l’uomo avanza di
moto uniforme verso prua, calcolare: a) quanto dista la prua da riva nell’istante
in cui l’uomo la raggiunge; b) l’energia spesa dall’uomo per spostarsi, sapendo
che il coefficiente di attrito sul fondo della barca è μ = 0,3
[1,2 m; 1,41 kJ]
18.51. Un blocco cubico di lato l = 3 m e massa M = 100 kg è fermo come in
figura con un vertice nell’origine degli assi; un uomo di massa m = 70 kg
inizialmente fermo in A, si muove verso B con velocità costante v = 40 cm/s.
Calcolare, trascurando ogni attrito, a) dove si troverà lo spigolo destro del cubo
quando l’uomo è giunto in B, b) con quale velocità si sta muovendo il blocco
quando l’uomo è arrivato in B.
[1,24 m; 16,5 cm/s]
573
18.52. Due sferette, una di massa doppia dell’altra, con velocità v1 e v2 (v1 >
v2) si inseguono e si scontrano centralmente lungo l’asse x. Dopo l’urto la
prima sferetta dimezza la velocità. a) Ricavare la nuova velocità della seconda
sferetta in funzione di v1 e v2; b) dire per quale valore di v2 l’urto è
perfettamente elastico.
[v 1 + v2; v 1/4]
18.53. Una sferetta di massa m = 50 g urta contro una parete rigida con velocità
v1 = 30 m/s che forma un angolo = 30° con l’orizzontale e vi rimbalza a un
angolo = 45°. Se nell’urto la pallina perde il 50% della propria energia cinetica,
calcolare: a) la velocità v2 con cui rimbalza la sferetta e b) la forza applicata alla
parete, sapendo che l’urto dura t = 6 ms.
[a) 21,2 m/s; b) 341,6 N, a un angolo di 15° con l’asse x]
18.54. Una particella di massa m = 10 g in moto con velocità v = 100 m/s lungo
l’asse x urta elasticamente una seconda particella di ugual massa ferma nel
punto O. Dopo l’urto le due particelle si allontanano formando con l’asse x
rispettivamente un angolo e – 2. Calcolare: a) l’angolo ., b) le energie
cinetiche delle due particelle dopo l’urto.
[ = 30°; K1 = 37,5 J, K2 = 12,5 J]
574
18.55. Una sferetta di massa m1 = 20 g si muove lungo l’asse x con velocità v1=
12 cm/s inseguendo una seconda sferetta di massa m2 = 30 g in moto nello
stesso verso con velocità v2 = 8 cm/s. L’urto è anelastico e la velocità relativa
della sferetta 1 rispetto alla 2 dopo l’urto è v = 3 cm/s. Calcolare: a) le velocità
delle due sferette dopo l’urto, b) l’energia dissipata nell’urto.
[11,4 cm/s, 8,4 cm/s; 4,2 μ J]
18.56. Due corpi di masse m1 ed m2 in moto lungo l’asse x con velocità v1 e v2
(< v1) si urtano anelasticamente proseguendo uniti. Ricavare l’espressione
dell’energia dissipata nell’urto e dire se esiste qualche caso particolare in cui
essa può essere nulla.
m1m 2
2
E d = 2 (m +m ) (v1 -v 2 ) .Ed = 0 quando v1 = v 2, ma in tal caso i corpi non 1
2
potranno urtarsi.
18.57. Un corpo puntiforme di massa m = 100 g con velocità iniziale vo = 10 m/s
urta frontalmente e anelasticamente a un’altezza h = 1 m dal suolo una parete
verticale, ricadendo a terra a una distanza d = 3 m dalla stessa.
Calcolare:a) l’impulso ricevuto dalla parete; b) la percentuale di energia
meccanica persa dal corpo tra la posizione iniziale (prima di toccare la parete) e
quella finale (quando tocca terra).
[0,34 N s; – 63,1%]
18.58. Una sferetta di massa m1 viene lanciata lungo l’asse x con velocità v
contro una seconda sferetta di massa m2 in quiete. Determinare, in funzione
delle quantità assegnate, l’espressione della massima quantità di calore Q che
si può liberare nell’urto, precisando la natura energetica dell’urto prevista.
575
m1m2v 2
Q
=
,
ipotizzando
un
urto
totalmente
anelastico.
2 ( m1 + m2 )
18.59. Un oggetto puntiforme in moto orizzontale con velocità vo urta
normalmente e anelasticamente una parete rigida a quota h dal suolo. Se esso
perde 1/4 della sua energia cinetica, ricavare l’espressione della distanza dalla
parete alla quale tocca terra.
d = v 0
3h 2 g 18.60. Un proiettile di massa m = 20 g penetra orizzontalmente in un blocco di
massa M >> m in quiete su un piano orizzontale liscio per un tratto d = 4 cm
impiegando t = 2 ms. Calcolare: a) la velocità del proiettile, b) l’energia
dissipata nell’urto, c) l’impulso ricevuto dal blocco, d) la forza esercitata dal
blocco sul proiettile.
[40 m/s; 16 J; 0,8 N s; 400 N]
18.61. Una sonda spaziale di massa m = 1 t viene messa in moto accendendo il
motore per un intervallo t = 50 s; in tale intervallo viene scaricato gas alla
velocità vr = 5 km/s e la velocità finale della sonda è v1 = 1200 m/s.
Trascurando il peso della sonda, calcolare la portata di massa del gas espulso.
[4,27 kg/s]
576
Cap. 6 – Dinamica dei sistemi
18.62. Una trave omogenea uniforme di lunghezza l = 3 m incernierata in O è in
equilibrio appesa in B a una molla ideale di rigidità k = 39,2 N/m che risulta
allungata di s = 6 cm, mentre un bambino di massa m = 40 kg è fermo sulla
trave in un punto C. Calcolare di quanto deve avanzare il bambino sulla trave
per portarla in posizione orizzontale.
[38,7 cm]
18.63. Un cilindro omogeneo di massa M e raggio R ruota attorno all’asse
baricentrale con velocità angolare iniziale o e posizione angolare iniziale o
quando viene sottoposto a un momento frenante Mo = – k , dove k è una
costante e la velocità angolare istantanea. Ricavare la legge oraria del moto
in funzione delle grandezze assegnate.
2k t 0M R 2
2
= 0 +
1 e MR 2k
18.64. Un metodo per calcolare il momento d’inerzia di un corpo di forma
irregolare rispetto all’asse baricentrale consiste nel sospenderlo a un filo
ideale, farlo ruotare di un certo angolo e misurare il periodo delle piccole
oscillazioni dopo averlo lasciato libero (pendolo di torsione). Sia T1 = (2,5 ±
±0,1) s tale periodo. Si prende poi un corpo campione di momento d’inerzia
noto, Io = (0,8 ± 0,01) kg m2 e lo si sospende allo stesso filo, ripetendo il
procedimento e trovandone il periodo delle piccole oscillazioni, T o = (1,6 ± ±0,1)
s. Calcolare: a) il momento d’inerzia del corpo irregolare, b) l’errore percentuale
più probabile della misura.
[1,95 kg m2, 14,9%]
577
18.65. Un cilindro omogeneo rotola dalla cima al fondo di un piano inclinato di
= 30°, raggiungendo al termine una velocità del centro di massa vCM = 4 m/s.
Calcolare: a) la lunghezza l del piano inclinato, b) l’accelerazione con cui scende
il cilindro, c) il tempo impiegato a percorrere il piano inclinato.
2
3 v CM
= 2, 45 m; = v CM / t = 3, 27 m / s 2 ; t = 2l / v CM = 1, 22 s l =
4g sin 18.66. a) Quale potenza media deve avere un motore per conferire a una sfera
omogenea di massa M = 2 kg e raggio r = 10 cm una velocità angolare = 40
giri/s in un tempo t = 15 s? b) Quanti giri ha compiuto la sfera in tale intervallo
di tempo?
2 2
7M r
t
= 58, 9 W, b)n =
= 300 giri a)W =
10t
2
18.67. Con riferimento al Problema 18.70, fissando l = 6 r, calcolare per quale
valore del rapporto M/m il pendolo composto in esame avrebbe lo stesso
periodo di un pendolo semplice di lunghezza l + r.
[18]
18.68. Supponendo la Terra sferica e omogenea, di massa mT = 5,98 1024 kg e
raggio r T = 6360 km, calcolare quale momento frenante è in grado di rallentare
il periodo di rotazione terrestre di 1 μs nell’arco di 24 h.
578
[9,42 1017 N m]
18.69. Un’asta omogenea uniforme di lunghezza l = 60 cm e massa M = 6 kg è
incernierata in O senza attriti a 2/3 della lunghezza e reca appese agli estremi
due masse puntiformi m = 2 kg e x incognita, mantenendosi in equilibrio.
Calcolare: a) il valore di x, b) il nuovo valore x’ quando la massa m viene appesa
nel punto C a 1/3 della lunghezza, c) il momento d’inerzia del sistema rispetto
all’asse passante per O nelle condizioni iniziali.
[7 kg, 5 kg, 0,84 kg m2 ]
18.70. Una sferetta di raggio r/2 urta orizzontalmente, frontalmente ed
elasticamente con velocità v una seconda sferetta di raggio r e dello stesso
materiale appesa in quiete al soffitto mediante un filo ideale di lunghezza l = 5
r. Esprimere: a) il valore di v in funzione di r perché in seguito all’urto la
sferetta ferma raggiunga, fermandovisi istantaneamente, la posizione B; b) la
velocità di rinculo v’ della prima sfera sempre in funzione di r.
[9
3 g r ; 7
3g r ]
18.71. Un blocco omogeneo di massa M = 0,4 kg è appeso al punto O mediante
un filo ideale di lunghezza l = 2 m ed è inizialmente in quiete in A. Una freccia
di massa m = 60 g scagliata con velocità v si conficca nel blocco e il sistema
entra in rotazione. Trascurando qualsiasi attrito, calcolare: a) per quale valore
di v il blocco si porta, fermandosi nella posizione B; b) il lavoro di perforazione
del blocco,c) che tipo di equilibrio è quello nella posizione B.
579
[48 m/s; 60,1 J; instabile]
18.72. Un uomo di massa m = 60 kg è in quiete sul bordo di una piattaforma di
massa M = 200 kg e raggio r che sta ruotando con velocità angolare costante =
15 rad/s attorno al proprio asse.
Se l’uomo si mette in moto radialmente con velocità costante v, a) ricavare,
trascurando gli attriti e considerando puntiforme l’uomo, l’espressione della
nuova velocità angolare in funzione della distanza x percorsa dall’uomo e b)
calcolarne il valore quando l’uomo è giunto nel centro della piattaforma.
[
= 0
(2m + M )r 2
2m ( r x )
2
+Mr
2
; 24
rad
]
s
18.73. Un’asta omogenea e uniforme lunga l = 1 m di massa M = 1 kg è appesa
verticalmente imperniata in P. Un proiettile di massa m = 10 g la colpisce
orizzontalmente nel centro di massa restandovi conficcato. Se l’asta in seguito
all’urto descrive un quarto di giro fermandosi per poi ricadere, calcolare: a) la
velocità del proiettile, b) il lavoro di perforazione.
580
[364,6 m/s; 660 J]
18.74. Un’asta e una sfera omogenee con la stessa massa M e tali che la
lunghezza l della prima uguaglia il diametro della seconda, ruotano con la
stessa velocità angolare costante attorno all’asse baricentrale. Calcolare i
rapporti:
a) tra i loro momenti d’inerzia baricentrali, b) tra i loro momenti angolari
rispetto all’asse baricentrale.
[5/6; 5/6]
Cap. 7 – Meccanica relativa
18.75. Un ragazzo fermo su un tappeto mobile lancia verticalmente una palla
con velocità vo = 6 m/s nell’istante in cui il tappeto accelera verso destra con
accelerazione aT = 2 m/s2. a) quale sarà il tempo di volo della palla? b) in quale
punto del tappeto ricadrà?
[a) 1,5 m alle spalle del ragazzo; b) 1,22 s]
581
18.76. Sul pianale di un camion è appoggiata una cassa il cui coefficiente di
attrito col pianale è μ = 0,8. Mentre il camion sta viaggiando con velocità v = 63
km/h, l’autista, per evitare di investire un cane, è costretto a frenare fino
all’arresto del veicolo. Supponendo che la sua decelerazione sia costante,
calcolare: a) la minima distanza di arresto perché la cassa non si sposti sul
pianale, b) il tempo di arresto del camion.
[19,5 m; 2,23 s]
18.77. Un pendolo semplice di lunghezza l oscilla in un ascensore fermo a terra
con periodo T 1; quando l’ascensore accelera verso l’alto con accelerazione
costante a = 2,3 m/s2, il periodo misurato dal passeggero diventa T 2 = 0,9 T1.
Calcolare l’accelerazione di gravità del luogo.
[9,805 m/s2]
18.78. Un pendolo conico è costituito da un corpo puntiforme sospeso a un
punto fisso O mediante un filo ideale di lunghezza l =1 m e posto in rotazione
in modo da compiere una traiettoria circolare di raggio r = 90 cm in un piano
orizzontale. Calcolare il periodo di tale pendolo conico.
[1,32 s]
18.79. Un treno, ciascuna carrozza del quale ha massa m =120 t sta viaggiando
alle alte latitudini nell’emisfero Nord su un binario disposto lungo un parallelo
a velocità v = 30 m/s. Calcolare la forza agente sulle rotaie e stabilire qual è la
rotaia maggiormente consumata per effetto di tale forza.
[524,9 N; quella più vicina al polo]
582
18.80. Un pendolo di Foucault compie un’oscillazione completa a Parigi (Lat.
48°52’) in 31 h 52 min. In quanto tempo compie l’oscillazione a Milano (Lat.
46°30’)? In quanto tempo ai poli?
[33 h 5 min; 24 h]
18.81. Al soffitto di un ascensore è appeso un dinamometro al quale è fissata
una massa m = 200 g. Calcolare quale peso indica il dinamometro a un
passeggero nei seguenti casi di moto dell’ascensore:a) salita con velocità
costante v = 3 m/s; b) discesa con la stessa velocità; c) per la rottura del cavo,
moto in caduta libera; d) salita con accelerazione costante a = 2 m/s2; e)
discesa con la stessa accelerazione.
[a) 1,96 N; b) 1,96 N; c) 0; d) 2,36 N; e) 1,56 N]
18.82. Una pulce si muove radialmente con velocità costante v R = 5 cm/s sul
piatto di un giradischi che sta ruotando con frequenza f = 33 giri/min. Calcolare
a quale distanza dal centro del piatto deve trovarsi la pulce perché la sua
accelerazione assoluta formi un angolo di 45° con la direzione radiale.
v
r
=
=
2,
9
cm
f
18.83. Due treni si muovono con la stessa velocità v in verso opposto su due
binari paralleli e sono lunghi complessivamente l = 200 m. Se essi impiegano t
= 5 s per superarsi, calcolare v.
[72 km/h]
18.84. Un nuotatore capace di nuotare con velocità vn = 1,8 km/h si tuffa in un
fiume largo l = 200 m con l’obiettivo di raggiungere la sponda opposta nel punto
esattamente antistante quello di partenza. Se la corrente ha velocità vc = 1,5
km/h, calcolare: a) in quale direzione deve tuffarsi, b) quanto tempo impiegherà
a raggiungere l’obiettivo.
[a) Controcorrente a un angolo di 33°33’ con le linee di corrente;
b) 12 min 4 s]
18.85. Un razzo viaggia lungo un parallelo con velocità v = 1000 km/h da ovest
verso est. Calcolare in modulo, direzione e verso l’accelerazione di Coriolis
agente su esso.
[aC = 4,05 cm/s 2, in direzione perpendicolare
all’asse terrestre e orientata verso l’asse stesso]
583
Cap. 8 – Fluidi
18.86. Un cilindro di sezione S = 100 cm2 galleggia in acqua ( = 1000 unità SI);
appoggiando sul cilindro un oggetto di massa m, esso affonda di un tratto s = 3
mm. Calcolare m.
[30 g]
18.87. Un cubetto di ghiaccio (densità gh = 920 unità SI) di spigolo a = 4 cm
galleggia in un bicchiere cilindrico di sezione S = 25 cm2 pieno d’acqua fino a
un’altezza h = 10 cm. Calcolare la nuova altezza h’ dell’acqua quando il cubetto
è completamente fuso.
[10 cm]
18.88. Una sferetta di ferro di densità 0 = 8000 unità SI e volume V0 = 6 cm3 è
immersa in acqua ( = 1000 unità SI) appesa a una molla ideale di rigidità k =
20 N/m mediante un filo ideale fissato al soffitto. Se la molla, in condizioni di
equilibrio, è allungata di un tratto x = 1 cm, calcolare la tensione del filo.
[T
= ( 0 ) V g k x = 0, 21 N]
18.89. Un cilindro omogeneo di legno di altezza h e densità = 950 unità SI
immerso in un liquido galleggia in modo che la parte emergente è pari a 3/4 h.
Calcolare la densità del liquido.
[3800 unità SI]
584
18.90. Un cilindro di legno di sezione S = 300 cm2 galleggia su un liquido;
appoggiandovi un corpo di massa m = 0,9 kg, il cilindro affonda di un ulteriore
tratto s = 2 cm. Calcolare la densità del liquido.
[ = m/(S s) = 1500 unità SI]
18.91. Una sferetta omogenea appesa a un filo ideale viene immersa dapprima
in un liquido di densità 1 = 2 g/cm3, quindi in un secondo liquido di densità
2 = 1 g/cm3. Se la tensione del filo nel secondo caso è doppia che nel primo,
calcolare la densità della sferetta.
[3 g/cm3]
18.92. Un blocco prismatico retto di densità = 900 unità SI e volume V = 0,2 l
è appeso a due identiche molle di rigidità k = 60 N/m galleggiando radente al
pelo libero dell’acqua e recando appesa nella parte inferiore mediante un filo
ideale una sferetta di volume V1= 5 cm3 e densità 1 = 5000 unità SI.
Calcolare: a) la tensione del filo, b) l’allungamento delle molle.
[0,196 N/m; 0]
18.93. Una sfera cava di ferro ( = 7800 unità SI) di diametro esterno d2 = 61
cm galleggia in acqua a Milano emergendo per metà. a) Calcolare il diametro
585
interno della sfera. b) All’equatore la spinta di Archimede sulla sfera varierà? in
che senso? c) Ai poli la sfera emergerà di più o di meno?
[59,7 cm; diminuisce; la linea di galleggiamento rimarrà costante]
18.94. Una sottile asta omogenea e uniforme di massa m = 40 g è appesa come
in figura a una molla ideale di rigidità k = 200 N/m e galleggia emergendo
esattamente per metà in un liquido di densità 1 in rapporto r = 4/3 con quella
dell’asta. Calcolare l’allungamento della molla.
mgr
= 0, 65 mm ]
[x =
4k
18.95. Una canna barometrica torricelliana contiene acqua per un’altezza h =10
cm al di sopra del mercurio. Se la pressione atmosferica è 90 kPa, quale sarà
l’altezza x della sottostante colonna di mercurio?
[66,8 cm]
586
18.96. Un tubo orizzontale di diametro h = 30 cm alimentato da un acquedotto
presenta un ugello di sezione a = 2 cm2 inclinato di = 30° sull’orizzontale.
Calcolare quale deve essere la portata di volume dell’acquedotto perché lo
zampillo del getto tocchi terra a distanza d = 6 m dall’inizio dell’ugello
[Q = a d
g
d sin 60° + 2h cos 30°
2
= 1, 58
l
s
]
18.97. Quale deve essere la portata di volume di un condotto perché da un foro
aperto in corrispondenza di una strozzatura di sezione A = 40 cm2 fuoriesca
uno zampillo alto h = 10 m?
[56 l/s]
18.98. Sulle pareti di un recipiente pieno d’acqua vengono praticati due
forellini di sezione trascurabile rispetto alla sezione di base rispettivamente a
distanza h1 = 20 cm e h2 = 80 cm dal pelo libero.
Supponendo che un rubinetto immetta acqua nel recipiente mantenendo
costante il livello del liquido mentre questo fuoriesce dai forellini e sapendo
che i due getti toccano terra nello stesso punto, calcolare:
a) l’altezza h del recipiente, b) la distanza d.
[h = 1 m; d = 80 cm]
18.99. Un silos cilindrico di sezione A = 1 m2 pieno di vino presenta sul fondo
un forellino di sezione a = 0,5 cm2. Il livello iniziale del liquido è h = 6 m; per
evitare di perdere il prezioso liquido, si pone sotto al silos una vasca di
capacità V = 40 l. In quanto tempo si riempirà tale vasca?
[5 h 35 min 39 s]
587
18.100. A quale altezza arriva lo zampillo fuoriuscente da un forellino praticato
in un condotto in cui scorre acqua in regime stazionario con velocità 14 m/s? A
quale altezza se il liquido è mercurio?
[10 m, la stessa]
18.101. Calcolare la pressione dinamica esercitata sulle pareti di un condotto
di sezione costante 1200 cm2 nel quale scorre acqua con portata di volume 100
l/s.
[347,2 Pa]
18.102. Il raggio dell’arteria aorta dell’uomo è 1 cm, mentre la portata di
volume corrispondente al flusso cardiaco è 5 l/min. Calcolare, supponendo un
regime stazionario, la velocità media del flusso sanguigno nell’aorta.
[26,5 cm/s]
18.103. In una miniera a profondità 200 m si verificano infiltrazioni d’acqua al
ritmo di 600 l/min. Quale potenza deve avere una pompa per garantire
l’asportazione di tutta l’acqua di infiltrazione?
[19,6 kW]
18.104. In un capillare di raggio r = 1 mm si ha un gradiente di pressione di 4
mmHg/cm. Calcolare la portata di volume quando in esso scorre un liquido con
viscosità 2 mPa s.
[10,4 cm3/s]
18.105. Un blocchetto cubico di legno di densità o = 950 unità SI galleggia su
un liquido emergendo per 2/3 del suo volume V. Calcolare la densità del
liquido.
[2,85 g/cm3]
18.106. Un oggetto pesa 100 N in aria e 75 N immerso in acqua. Calcolare la
densità relativa all’acqua dell’oggetto.
[ r = 4]
18.107. Se nell’esperimento di Torricelli il tubo barometrico viene inclinato a
45°, quale sarà la lunghezza l della colonna di mercurio?
[107,5 cm]
588
18.108. Un condotto di raggio r si suddivide in 4 condotti di raggio r/3. Se la
velocità media di un liquido omogeneo nel primo condotto è v, qual è la velocità
media in ciascuno dei condotti più piccoli ipotizzando un regime stazionario?
[9 v/4]
18.109. In una piccola arteria di raggio r = 4 mm la pressione relativa è p = 80
mmHg. Calcolare la tensione elastica delle pareti.
[21,3 N/m]
18.110. Un blocco di sezione a = 150 cm2 e massa m = 4 kg viene appoggiato su
un pistone mobile di sezione A = 1500 cm2. Quale pressione vi esercita?
[0,26 kPa]
18.111. In un ramo di un tubo a U si trova acqua, nell’altro mercurio. In
condizioni di equilibrio, quanto vale il rapporto tra l’altezza dell’acqua e quella
del mercurio, misurate rispetto alla superficie di separazione tra i due liquidi?
[13,6]
18.112. Un motore pompa 10 l/s di liquido a una pressione media di 2 atm in
un condotto orizzontale. Calcolare il lavoro compiuto in 2 s.
[4,04 kJ]
18.113. Un’arteria nella quale scorre del sangue con velocità v si biforca in due
arteriole ciascuna di raggio pari alla metà di quello dell’arteria principale. Quale
sarà la velocità media del sangue nelle due arteriole?
[2 v]
18.114. La zattera del Problema 8.62. ha spessore d = 25 cm ed è costruita con
un materiale di densità 0 = 960 unità SI. Calcolare il periodo delle piccole
oscillazioni della zattera dopo la perdita del carico.
T = 2
589
0d
= 0, 98
g
s
18.115. Quando un sommergibile si immerge a 120 m di profondità, quale
pressione devono esercitare le pompe per espellere acqua dai compartimenti
stagni, se la densità dell’acqua marina è 1030 unità SI?
[1,31 MPa]
Cap. 9 – Gravitazione
18.116. Calcolare a quanti kilometri dalla superficie terrestre un satellite
lanciato da Terra con velocità v = 1 km/s dimezza la propria velocità. (Assumere
i seguenti valori: raggio terrestre: 6,36 Mm; massa terrestre: 5,98 1024 kg.)
[38,3 km]
18.117. Un satellite è detto geostazionario quando il suo periodo di
rivoluzione attorno alla Terra è di 24 h. Supponendo che la sua orbita sia
circolare, calcolare: a) il raggio dell’orbita, b) la velocità orbitale.
[42300 km; 3,1 km/s]
18.118. A quale distanza massima da Terra può arrivare un razzo lanciato
verticalmente verso l’alto con velocità iniziale v 32=1800 km/h? Trascurare la
resistenza dell’atmosfera e assumere per la massa e il raggio terrestre i
seguenti valori: mT = 5,98 1024 kg, r T = 6,36 106 m.
[12,7 km]
18.119. Tre masse identiche m = 20 g sono in quiete nei vertici A, B, C di un
triangolo equilatero di lato l = 40 cm. Se la massa posta in A viene lasciata
libera, con quale velocità passerà dal punto medio M di BC?
[3,66 μm/s]
18.120. Un satellite artificiale di massa m = 100 kg si trova in orbita circolare
attorno alla Terra a una distanza dalla superficie terrestre h = 1140 km;
sapendo cha la massa e il raggio terrestri valgono rispettivamente mT = 5,98 1024 kg ed r = 6,36. 106 m, calcolare:
T
590
a) la velocità periferica del satellite, b) la forza centripeta agente su esso, c) il
suo peso in orbita, d) la sua massa in orbita, e) l’energia totale, f) la gravità in
orbita.
[7,29 km/s; 709,1 N; 709,1 N; 100 kg; – 2,66 GJ; 7,1 m/s 2]
18.121. Ricavare l’espressione dell’energia potenziale derivante da una forza
attrattiva radiale di modulo F = k/r4.
k
]
[U = 3 r3
18.122. Tre masse uguali m = 3 kg si trovano in quiete ai vertici di un triangolo
equilatero di lato l = 60 cm. Calcolare: a) la forza gravitazionale agente su una
quarta massa M = 10 kg posta al centro del triangolo, b) il minimo lavoro che si
deve compiere per separare a distanza infinita le quattro masse, precisando il
significato dell’aggettivo "minimo".
[0; 20,3 nJ; il lavoro è minimo se le masse separate
a distanza infinita sono in quiete]
18.123. Calcolare di quanto varia percentualmente l’accelerazione di gravità di
un pianeta sferico di raggio r salendo dal livello del mare a una quota doppia
del raggio del pianeta.
[– 75%]
18.124. Un pendolo semplice sulla Terra ha un periodo T = 4 s. Se lo si porta
su un pianeta sferico avente raggio doppio della Terra e densità media pari a un
quarto di quella terrestre, calcolare: a) l’accelerazione di gravità di tale pianeta
e b) il periodo T’ del pendolo.
[4,9 m/s 2 5,66 s]
18.125. Un pianeta di massa M ha un satellite di massa m che percorre
un’orbita circolare di raggio r = 20000 km e periodo T = 5 104 s. Supponendo m
<< M, calcolare la massa M.
[1,89 1024 kg]
18.126. Se la massa della Terra raddoppiasse senza alcuna variazione del
raggio, ipotizzandola sferica e omogenea, stabilire: a) la nuova durata dell’anno
solare, b) la nuova accelerazione di gravità terrestre, c) la nuova distanza TerraSole, d) la nuova durata del mese lunare.
[a) inalterata; b) 19,6 m/s 2; c) inalterata; d) 19 giorni 9 h]
18.127. Calcolare l’intensità del campo gravitazionale terrestre: a) a 6360 km di
quota, b) a 3180 km di profondità all’interno della Terra.
[a) 2,45 N/kg; b) 4,88 N/kg]
591
18.128. Sapendo che il raggio terrestre vale rT = 6360 km e supponendo che
l’atmosfera terrestre sia alta h = 1000 km, calcolare la massa dell’atmosfera
terrestre.
[6,02 1018 kg]
Cap. 10 – Termologia
18.129. Un barometro è munito di una scala graduata in ottone; alla
temperatura t1 = 27 °C l’altezza della colonna di mercurio letta sulla scala è h1
= 751,3 mm. Calcolarne l’altezza a to = 0 °C, sapendo che il coefficiente di
dilatazione lineare dell’ottone è =1,9.10–5°C–1, mentre quello del mercurio è [h = h1 [(1– t1 ( – )] = 748,0 mm]
= 1,82 10–4 °C–1.
18.130. L’acqua di uno stagno (densità = 103 unità SI) si trova a temperatura
t1 = 0 °C, mentre la temperatura esterna dell’aria è t2 = –14 °C. Quale spessore
di ghiaccio si forma nell’intervallo T = 24 h contato a partire dall’istante in cui
l’acqua comincia a solidificare? La conducibilità termica
del ghiaccio è k = 2,1 unità SI, il calore di fusione del ghiaccio è c f = 80 cal/g.
[x =
]
T (t1 t2 ) k
= 8,7 cm
cf
18.131. Mescolando in un calorimetro 8,0 g di limatura di ferro (c 1 = 0,12 cal
/(g °C) e 12,0 g di l limatura di alluminio (c2 = 0,21 cal /(g °C)) alla stessa
temperatura, qual è il calore specifico della miscela ottenuta?
cal
[0,17
]
g° C
18.132. Un chiodo di massa m = 10 g inizialmente in quiete si muove lungo
l’asse x spinto da una forza F = 0,02 t in unità SI. Dopo t = 10 s il chiodo
incontra un blocco di ghiaccio a 0°C e vi penetra fermandosi in esso. Calcolare
la massa di ghiaccio fusa, se la pressione esterna è 1,0 atm e il calore di
fusione del ghiaccio è cf = 80 cal/g.
[ mgh =
592
F dt 0
4 m cf
10
2
= 0,15 g ]
18.133. Un cilindro di ottone di sezione S = 20 cm2 contiene un volume V1=
200 cm3 di glicerina compressa da un pistone di peso P = 600 N. Trascurando la
dilatazione termica dell’ottone, se si riscalda il cilindro da t1 = 60 °C a t2 = 160
°C, calcolare:
a) l’aumento di volume V della glicerina, il cui coefficiente di dilatazione cubica
è = 5,3 10–4 °C–1, b) il lavoro compiuto dalla glicerina sul pistone, c) la
quantità di calore assorbita dalla glicerina, se la sua densità è = 1260 unità SI
e il suo calore specifico c = 0,5 cal/(g°C).
V (t t )
pV
3
= 3, 08 J; c) Q = 12, 6 kcal a) V = 1 2 1 = 10, 27cm ; b) L =
S
1 + t1
18.134. Due oggetti isolati mobili nella stessa direzione e nello stesso verso si
urtano procedendo uniti dopo l’urto. Le masse, le temperature, le velocità e i
calori specifici dei due oggetti sono: m1 = 2,0 kg, m2 = 4,0 kg, t1 = 20 °C, t2 = 24
°C, v1 = 50 m/s, v2 = 80 m/s, c1 = 1,0 cal/(g°C), c2 = 0,2 cal/(g°C). Supponendo
nullo il lavoro di deformazione e trascurando qualsiasi dispersione di calore,
calcolare la temperatura finale dell’oggetto risultante.
(m1v1 +m 2v 2 )2 1
1
m1v12 m 2v 22 +m1c1t1 +m 2c2t2
2
2
t = 2(m1 +m 2 )
=
21,1
°C
m1c1 +m 2c2
18.135. Calcolare la velocità che deve avere un proiettile di piombo (c = 0,3
cal/g°C) per poter fondere urtando anelasticamente una lastra di acciaio. La
temperatura del proiettile è t1 = 27 °C, quella di fusione del piombo è tf = 327 °C
e il calore di fusione del piombo è cf = 5 cal/g.
[ v = 2( c t + c f = 892 m
]
s
18.136. Qual è il calore specifico di un oggetto di massa m = 2 kg che
inizialmente alla temperatura to = 350°C, immerso in un calorimetro in1 l di
acqua a t1 = 20°C ne fa innalzare la temperatura a t2 = 50°C ?
[0,05 cal/g °C]
18.137. Ricavare la relazione tra il calore specifico c riferito all’unità di massa
e quello molare c’.
[c’ = M c]
593
Cap. 11 – Teoria cinetica dei gas
18.138. Calcolare il numero di molecole di azoto contenuto in un recipiente di
volume V=1,0 l a temperatura T = 300 K e pressione p = 10–6 mmHg.
pV
= 3, 2 1013 N =
kT
18.139. Calcolare la velocità quadratica media delle molecole di anidride
carbonica (M = 44 g/mol) contenute in un recipiente a p = 2,0 atm e il cui
affollamento molecolare è N = 1019 molecole/cm3.
[910,6 m/s]
18.140. M = 12 g di un gas perfetto triatomico a T = 1000 K hanno un’energia
interna U = 16,6 kJ. Calcolare il peso molecolare M del gas.
[18 g/mol]
18.141. 1 mol di gas ideale biatomico ha energia interna di U = 6,23 kJ. Se la
velocità quadratica media delle molecole del gas è, alla stessa temperatura, vqm
= 1,5 km/s, calcolare la massa m di una molecola.
[5,52 10–27 kg]
18.142. Un recipiente cilindrico di sezione S = 200 cm2 munito di un pistone di
massa m = 3,0 kg contiene ossigeno, il cui raggio molecolare è r = 0,18 nm. Se
la velocità quadratica media delle molecole è vqm = 1 km/s, calcolare il cammino
libero medio secondo Clausius, C.
[22,2 μm]
18.143. In un recipiente a pareti rigide adiatermane inizialmente vuoto viene
introdotto un gas ideale di peso molecolare M = 4 g/mol le cui molecole hanno
tutte la stessa velocità v = 2 km/s. Calcolare la temperatura del gas una volta
raggiunto l’equilibrio termico.
[641,8 K]
18.144. Calcolare l’energia cinetica traslazionale di una mole di ammoniaca
NH 3 ideale alla temperatura di 300 K.
[3,74 kJ]
18.145. Un gas perfetto è una miscela di due gas, uno dei quali ha molecole di
raggio r1 = 2.10–8 cm; il cammino libero medio delle molecole del primo gas è 1
= 2.10–5 cm, mentre quello delle molecole del secondo, nelle stesse condizioni
594
di temperatura e pressione, è 2 = 8.10–5 cm. Calcolare a quale distanza devono
trovarsi i centri di due molecole della miscela perché possa aver luogo un urto
nei seguenti casi:
a) le due molecole sono del primo gas, b) le due molecole appartengono al
secondo gas, c) le due molecole appartengono una al primo e una al secondo
gas.
[0,4 nm; 0,2 nm; 0,3 nm]
18.146. Un uomo ha un volume V = 80 l. Calcolare in unità SI la spinta di
Archimede agente sull’uomo in aria a temperatura t = 20 °C e pressione p =1
atm, sapendo che il peso molecolare dell’aria, considerata gas perfetto, è M =
29 g/mol.
[0,94 N]
Cap. 12 – Primo principio della termodinamica
18.147. Calcolare la variazione di energia interna di una mole di gas perfetto
monoatomico se il gas si riscalda di T =100 K a) in una trasformazione
isocorica, b) in una isobara, c) il rapporto tra le due quantità di calore
necessarie.
[1,25 kJ; 1,25 kJ; 0,6]
18.148. Un gas perfetto è racchiuso in un recipiente cilindrico A nel quale può
scorrere senza attrito un pistone pesante. Aprendo la valvola R, il gas si
espande in un secondo recipiente B, inizialmente vuoto, fino al raggiungimento
dell’equilibrio termodinamico. Supponendo che le pareti siano rigide e
adiatermane e che l’espansione sia lentissima, si dica:
a) se la trasformazione è o meno reversibile,
b) se al termine del processo la temperatura del gas è aumentata, diminuita o è
rimasta invariata.
[irreversibile; aumentata]
595
18.149. Un gas viene compresso in condizioni identiche dal volume V1 al
volume V2, una volta rapidamente, una volta lentamente. In quale caso è
maggiore il lavoro compiuto sul gas?
[nella compressione rapida]
18.150. Se un gas perfetto pentaatomico dimezza il volume mentre quintuplica
la pressione, calcolare: a) l’esponente politropico, b) il calore specifico molare.
[2,32; 2,24 R]
18.151. Un gas perfetto contenuto in un cilindro chiuso da un pistone di
massa trascurabile riceve una quantità di calore Q = 400 J, mentre il pistone si
sposta e il volume aumenta. La temperatura del gas resta costante e il lavoro
compiuto viene utilizzato solo per sollevare una massa m = 80 kg, calcolare a
quale altezza essa può essere portata.
[0,51 m]
18.152. Se si comprime adiabaticamente e reversibilmente un gas ideale, esso:
a) si raffredda,
b) diminuisce il volume,
c) mantiene inalterata la velocità quadratica media,
d) compie lavoro sull’esterno,
e) mantiene costante l’energia interna.
Quali risposte cambiano e in che modo, se il processo è irreversibile?
[falso; vero; falso; falso; falso; nessuna]
18.153. Un gas passa da uno stato con U1 = 600 kJ a uno stato con U2 =200 kJ
compiendo un lavoro L = 300 kJ. Calcolare la quantità di calore ricevuta dal gas
nel caso di processo a) reversibile, b) irreversibile.
[a) –100 kJ; b) –100 kJ]
Dal primo principio, abbiamo: Q = L + U = L + U2 – U1 = 300 + 200 –600 = –100 kJ.
Il gas non assorbe, ma cede calore. Il risultato è indipendente dalla reversibilità del
processo, perché la forma del primo principio da noi utilizzata vale anche per
processi irreversibili.
18.154. Un gas perfetto poliatomico espande isotermicamente da V1 = 0,1 m3 a
V = 0,3 m3 e la pressione finale è p = 2.10 5 Pa. Calcolare:
2
2
a) l’aumento di energia interna, b) il lavoro compiuto dal gas, c) la quantità di
calore assorbita.
[0; 65,9 kJ; 65,9 kJ]
596
18.155. Ricavare il coefficiente di comprimibilità di un gas perfetto alla
pressione p = 2 atm in una trasformazione reversibile di equazione T V2=
costante.
6
1
[ 3, 3 10 Pa ]
18.156. Si dice che l’acqua è la sostanza con il più elevato calore specifico;
tuttavia, esistono trasformazioni politropiche di gas perfetti nelle quali il calore
specifico molare supera quello dell’acqua. Ricavare per quale minimo valore del
coefficiente politropico k ciò si verifica per l’idrogeno.
[k > 0,85]
18.157. L’energia interna di un gas è data da U = a ln (T/T o) + b ln (p/p o), dove
a = 3 kJ, b = 7 kJ. Se il gas viene riscaldato da T1 = 250 K a T2 = 500 K,
assorbendo la quantità di calore Q = 14,33 kJ e compiendo un lavoro L =
= 4,56 kJ, quale sarà la variazione percentuale di pressione?
[200 %]
18.158. Se la pressione atmosferica cambia da p1 = 983 hPa a p2 = 1003 hPa,
qual è stata la variazione di energia interna dell’aria contenuta in un locale di
volume V = 50 m3?
[250 kJ]
18.159. Il calore specifico molare di un gas tetraatomico varia in una
trasformazione secondo la legge c = (20 + 500/T) J/(mol K). Calcolare il lavoro
di 1 mol di gas nel riscaldamento da T 1 = 200 K a T 2 = 544 K.
[ –1,2 kJ]
18.160. A parità di variazione di volume, partendo dallo stesso stato iniziale,
in quale delle seguenti trasformazioni reversibili di un gas perfetto il gas
compie la maggior quantità di lavoro: a) adiabatica, b) isobara, c) isotermica ?
[isobara]
Cap. 13 – Cicli. Entropia
18.161. Un ciclo di profilo ellittico viene percorso in senso antiorario nel piano
(p, V); calcolare la quantità di calore assorbita complessivamente nel ciclo dal
fluido operante.
[52,9 J]
597
18.162. 1 mol di gas perfetto monoatomico subisce una compressione
irreversibile dalla pressione p1 = 3 atm alla pressione p2 = 6 atm; se il volume
finale è uguale a quello iniziale (V = 3 l), calcolare, sapendo che durante il
processo vengono fornite al gas Q = 1209 J:
a) il lavoro compiuto sul gas, b) la variazione di energia interna, c) la variazione
di entropia del gas.
[–154,5 J, 1,36 kJ, 8,64 J/K]
18.163. Calcolare il rendimento e il fattore di qualità del ciclo reversibile
eseguito da un olio combustibile indicato in figura.
[50%, 1]
18.164. 1 mol di gas perfetto monoatomico è contenuta in un recipiente
adiatermano sigillato. Una resistenza libera calore all’interno del gas e la
variazione di energia interna è U = 8 kJ. Calcolare la variazione di entropia del
gas, sapendo che l’energia interna iniziale vale U i = 4 kJ.
[13,7 J/K]
598
18.165. Un recipiente a pareti metalliche rigide e sottili è diviso in due parti
diverse da un setto; nella prima vi sono n1 = 2 mol, nella seconda n2 = 4 mol di
gas perfetti, differenti tra loro, ma alla stessa temperatura e pressione.
Calcolare la variazione di entropia del sistema dei due gas dopo aver tolto il
setto.
[31,7 J/K]
18.166. L’entropia di un sistema termodinamico varia con la temperatura
secondo la legge S = a + b T, con b = 5 J /K2. Se il sistema viene portato da T1 =
290 K a T 2 = 310 K, quale quantità di calore assorbirà?
[30 kJ]
18.167. Calcolare: a) la variazione di entropia di 1 mol di gas perfetto che,
espandendo isotermicamente a temperatura T = 400 K, compie un lavoro L =
800 J; b) il rapporto di espansione tra il volume finale e quello iniziale.
[2 J/K, 1,27]
18.168. In un processo isotermico reversibile a T = 350 K, un olio compie un
lavoro L = 80 J, mentre la sua energia interna aumenta di U = 7,5 J. Calcolare
la variazione di entropia dell’olio.
[0,25 J/K]
18.169. A quale temperatura fonde un blocco di ghiaccio compresso con un
peso che lo sottopone alla pressione p = 300 atm? (densità del ghiaccio: 920
unità SI; calore di fusione: 80 cal/g).
[– 2,15 °C]
18.170. Calcolare la variazione di entropia di 2 mol di gas perfetto poliatomico
durante una trasformazione di equazione p T 2 = costante nella quale il volume
del gas si dimezza.
[– 23 J/K]
18.171. Una macchina termica reversibile opera tra tre sorgenti alle
temperature T1= 300 K, T2 = 400 K e T3 = 500 K, cedendo in ogni ciclo la
quantità di calore Q1 = 300 cal alla prima sorgente e assorbendo dalla terza
sorgente la quantità di calore Q3 = 500 cal. Calcolare il rendimento di tale
macchina.
[40 %]
18.172. Una macchina termica di Carnot compie in un ciclo un lavoro L = 10 kJ.
Se la massima differenza di entropia tra due punti del ciclo è S = 100 J/K,
qual è la differenza tra le due temperature di lavoro?
[100 K]
599
18.173. Una centrale termoelettrica consuma una massa di carbone c = 1,5
t/h; se il potere calorifico del carbone è p = 32 MJ/kg e la potenza della
centrale è W = 1,4 MW, calcolare il rendimento della macchina.
[10,5 %]
Cap. 14 – Gas reali. Potenziali termodinamici
18.174. Una massa m = 10 g di azoto subisce un’espansione isotermica
reversibile a temperatura T = 500 K nel corso della quale la pressione si
dimezza. Calcolare la variazione della funzione di Gibbs.
[– 1,03 kJ]
18.175. Una certa quantità di gas biatomico perfetto viene fatta espandere
reversibilmente e adiabaticamente dallo stato A (pA = 2 atm, VA = 1 l) allo stato
B (VB = 3 l). Calcolare la variazione di entalpia del gas.
[– 251 J]
18.176. 1 mol di gas perfetto subisce un processo isotermico reversibile a
temperatura T = 300 K nel corso del quale il volume raddoppia. Calcolare la
variazione di energia libera del gas.
[– 1,73 kJ]
18.177. 1 mol di azoto (costante di van der Waals a = 1,39 l2 atm/mol2)
espande nel vuoto dal volume Vi = 1 l al volume Vf = 10 l. Calcolarne la
variazione di temperatura.
[– 6,1 K]
600
18.178. In una isotermica reversibile di un gas perfetto a temperatura T = 400
K il potenziale di Gibbs subisce una variazione G = –400 J. Calcolare: a) la
variazione di entropia del gas e b) la quantità di calore scambiata con l’esterno.
[1 J/K, 400 J]
18.179. Calcolare la quantità di calore che si deve fornire a una certa quantità
di ossigeno perfetto in un processo isobarico perché esso subisca un aumento
di entalpia H = 104 J.
[Ovviamente 104 J, dato che la variazione di entalpia coincide con la quantità
di calore scambiata in un processo isobarico]
Cap. 15 – Onde meccaniche
18.180. Una corda di massa m = 0,5 g e lunghezza l = 90 cm è vincolata per un
estremo a un supporto fisso e per l’altro al rebbio di un diapason che vibra con
frequenza f = 340 Hz. Calcolare la tensione alla quale deve essere sottoposta la
corda per poter vibrare con la sua frequenza fondamentale.
[208,1 N]
18.181. La frequenza di vibrazione di un diapason è 290 Hz. Calcolare la
lunghezza d’onda del suono emesso in aria a 25 °C, sapendo che la velocità del
suono in aria aumenta, a partire da 0 °C, di 0,6 m/s per ogni grado di aumento
della temperatura.
[1,2 m]
18.182. Calcolare: a) frequenza e b) lunghezza d’onda del suono prodotto da
una sirena che ha un disco con 50 fori che ruota a 1200 giri/min. (La velocità
del suono è 344 m/s).
[1000 Hz; 0,344 m]
18.183. Un’onda si propaga in una corda tesa con equazione, in unità SI:
y = 0,4 cos (0,2 x – 16 t).
Calcolare:
a) la lunghezza d’onda, b) la frequenza, c) la velocità di propagazione, d)
l’ampiezza, e) la massima velocità trasversale delle particelle della corda.
[31,4 m, 2,55 Hz, 80 m/s, 0,4 m, 6,4 m/s]
601
18.184. Ipotizzando un meccanismo di propagazione adiabatico, calcolare il
rapporto tra le velocità del suono in due gas perfetti alla stessa temperatura,
uno tetraatomico con peso molecolare 17 g/mol e l’altro monoatomico con peso
molecolare 87 g/mol.
[2,02]
18.185. Una corda fissa agli estremi è lunga l = 0,99 m e ha massa m =1 g. Se
essa vibra in tre segmenti con una frequenza f = 500 Hz, calcolarne la tensione.
[110 N]
18.186. Un’onda si propaga in una corda di densità lineare 40 g/m tesa lungo
l’asse x. Se la sua equazione in unità SI è
y = 0,2 sin (3 x + 0,6 t)
calcolare: a) la tensione della corda, b) la massima accelerazione trasversale.
[1,6 mN; 7,2 cm/s2]
18.187. Un’onda sonora piana ha in aria a 20 °C intensità I =10,0 W/m2.
Calcolare la forza esercitata da tale onda su una parete di superficie S = 5 m2,
supponendo incidenza normale e assumendo che la velocità dell’onda alla
suddetta temperatura sia v = 343,5 m/s.
[F = I S/v = 146 mN]
18.188. La lunghezza d’onda del suono emesso da un diapason in aria è =
1,20 m quando la temperatura dell’aria è 20 °C. Se la velocità di propagazione
del suono in aria a 0 °C è v0 = 332 m/s, calcolare la frequenza del diapason.
[286,6 Hz]
18.189. Ipotizzando per l’elio (M = 4 g/mol) un meccanismo di propagazione del
suono adiabatico, calcolare la velocità del suono in tale gas a temperatura 800
°C e pressione 2,3 105 Pa.
[1,93 km/s]
18.190. Un ascoltatore vuole stimare a quale distanza d da lui è caduto un
fulmine misurando il tempo trascorso tra l’osservazione del lampo e la
ricezione del rumore del tuono, t = 4 s. Se l’aria è considerata un gas perfetto
biatomico e la sua temperatura è T = 280 K, calcolare d ipotizzando un
meccanismo di propagazione adiabatico.
[1,34 km]
602
Cap. 16 – Errori
18.191. In una misura di viscosità di un liquido si lascia cadere in esso una
sferetta e si misura la velocità costante che essa raggiunge dopo un certo
tratto di caduta. Se il raggio della sferetta viene misurato con una precisione
dell’1%, la velocità limite con una precisione del 2%, la densità della sferetta e
quella del fluido in cui si muove con una precisione dell’1%, ritenendo nota con
precisione assoluta l’accelerazione di gravità, da quale errore percentuale sarà
affetta la misura del coefficiente di viscosità del liquido?
[3,16%]
18.192. Un corpo di volume 1 l viene pesato in aria con una bilancia a piatti e
risulta avere una massa di 800 g. Se i pesi campione usati sono di rame
(densità 8800 unità SI), calcolare a) la vera massa del corpo, b) l’errore
percentuale commesso.
[801,2 g; 0,15 %]
18.193. In una misura del coefficiente di viscosità di un liquido in un capillare,
si misura il raggio del capillare con un errore percentuale dell’1%, la lunghezza
dello stesso con un errore percentuale dello 0,5%, la differenza di pressione
agli estremi con un errore percentuale dell’1,5% e la portata di volume con un
errore percentuale del 2%. Da quale errore percentuale sarà inficiata la misura
di ?
[4,74%]
18.194. Un pianeta di massa M ha un satellite di massa m che percorre
un’orbita circolare il cui raggio e il cui periodo sono noti entrambi con un errore
percentuale dell’1% Supponendo m « M, qual è l’errore percentuale con cui
viene misurata la massa M?
[3,61%]
18.195. Un ascoltatore vuole stimare a quale distanza d da lui è caduto un
fulmine misurando il tempo trascorso tra l’osservazione del lampo e la
ricezione del rumore del tuono, t = (4 ± 0,1) s. Se l’aria è considerata un gas
perfetto biatomico di peso molecolare M = (29 ± 0,1) g/mol e la sua temperatura
è T = (280 ± 0,4) K, calcolare: a) la distanza d ipotizzando un meccanismo di
propagazione adiabatico, b) l’errore percentuale da cui è affetta la stima,
supponendo noti con precisione molto alta l’esponente adiabatico dell’aria e la
costante universale dei gas perfetti.
[1341 m; 2,60 %]
603
Cap. 17 – Calcolo dimensionale
18.196. Ricavare le dimensioni del momento angolare in un sistema metrico
che adotta come grandezze fondamentali la forza, la frequenza e l’energia.
[ [P] = [f –1] [E] ]
18.197. Ricavare le dimensioni della forza nel sistema metrico che adotta come
grandezze fondamentali il momento d’inerzia, la densità e la potenza.
[[F]=[I
2/15
] [
1/5
] [W
2/3
]]
18.198. Individuare quale grandezza è espressa nel SI dalla relazione
x =
K V QV ,
Ia
nella quale K è un’energia cinetica, V un volume, QV una portata di volume, I
un momento d’inerzia, una densità e a un’accelerazione.
[[x] = [M L2 T–1], quindi
si tratta di un momento angolare]
18.199. Ricavare l’espressione dimensionale della pressione nel sistema
metrico che adotta come grandezze fondamentali la viscosità, la forza e la
velocità.
[[p] = [
2
] [F
–1
2
] [v ]]
18.200. Tra le seguenti terne di grandezze fisiche, quali possono essere
assunte come terne metriche per la costruzione di un sistema metrico
coerente?
a) momento meccanico – lavoro – velocità angolare
b) massa – energia cinetica – velocità
c) momento angolare – momento d’inerzia – periodo
d) rigidità – tensione superficiale – accelerazione
e) potenza – momento meccanico – momento d’inerzia.
[nessuna]
604












