Semiconduttori

PORTATORI ALL’EQUILIBRIO NEL SILICIO INTRINSECO.
Le proprietà elettriche dei semiconduttori dipendono in modo sostanziale dalla concentrazione di
cariche mobili negative e positive presenti, dette portatori di corrente o semplicemente portatori.
In un semiconduttore i portatori sono sia gli “elettroni presenti nella banda di conduzione”, sia
i buchi o lacune della banda di valenza;
♦ gli elettroni di conduzione si addensano verso i livelli inferiori della banda di conduzione;
♦ i buchi o lacune della banda di valenza si addensano verso i livelli superiori della banda di
valenza.
In un semiconduttore in condizioni di equilibrio termico, la distribuzione di elettroni e lacune lungo
l’asse delle energie è determinata dall’energia termica, quindi dalla temperatura del solido e da
nessun’altra fonte esterna di energia.
SEMICONDUTTORE INTRINSECO: dicesi intrinseco un semiconduttore puro nel quale la
generazione di un elettrone di conduzione implica la rottura di un legame covalente tra atomi del
semiconduttore e quindi la creazione di un buco di valenza o lacuna.
In un semiconduttore intrinseco la concentrazione di elettroni di conduzione
eguaglia la concentrazione di buchi di valenza detti lacune:
n = p =ni
ove ni è detta concentrazione di portatori intrinseci.
La concentrazione d’equilibrio ni è il risultato della compensazione di due meccanismi competitivi:
♦ uno di generazione di coppie elettrone di conduzione − buco di valenza, tanto più rapido quanto
più elevata è la temperatura e l’energia termica fornita dal cristallo per attivare il processo di
salto di un elettrone dalla banda di valenza a quella di conduzione;
♦ l’altro è un meccanismo di ricombinazione tanto più probabile quanto maggiore è il numero di
elettroni di conduzione e buchi di valenza.
In condizione di equilibrio le velocità dei due processi sono uguali: tante coppie si creano
nell’unità di tempo quante se ne ricombinano.
Se aumenta la temperatura, cresce il ritmo del processo di generazione e l’equilibrio si ristabilisce
quando il numero di coppie è aumentato tanto da incrementare la probabilità di ricombinazione fino
a compensare quella di generazione. Ci si aspetta perciò che la concentrazione di portatori intrinseci
aumenti sensibilmente con la temperatura.
Il prodotto n·p all’equilibrio dipende solamente dalla temperatura T, espressa in gradi Kelvin, e
dall’ampiezza EG del “gap”, espressa in eV (elettronvolt), fra la banda di valenza e la banda di
conduzione ed è perciò una quantità caratteristica di ogni semiconduttore.
Riferendoci ad un semiconduttore intrinseco, si ottiene:
n·p =ni2
Questa relazione, di fondamentale importanza in tutta la teoria dei semiconduttori, definisce la
condizione di equilibrio di un semiconduttore.
Il valore della concentrazione di portatori intrinseci alla temperatura ambiente è data da:
ni = 1,45·1010 cm− 3
ni = 2,40·1013 cm− 3
per il silicio ( Si )
per il germanio ( Ge )
Dalla relazione di equilibrio deriva che per il silicio, alla temperatura ambiente (27°C = 300°K),
vale la posizione seguente:
n·p =ni2 = 2,1·1020 cm−6
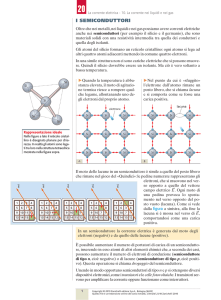
PORTATORI ALL’EQUILIBRIO NEL SILICIO DROGATO.
SEMICONDUTTORE ESTRINSECO: dicesi drogato o estrinseco un semiconduttore contenente
certi tipi d’impurezze che ne alterano la struttura elettronica. In un campione di silicio o germanio
contaminato con impurezze pentavalenti come arsenico, fosforo o antimonio, si crea la situazione
descritta in figura 1:
¾ l’atomo pentavalente sostituisce un atomo del semiconduttore in modo tale che uno dei cinque
elettroni di valenza dell’impurezza, non trovandosi coinvolto in alcun legame covalente, resta
pressoché libero di muoversi.
Questo corrisponde, in uno schema a bande, alla formazione di un livello localizzato nel “gap” e
prossimo alla banda di conduzione. È sufficiente una piccola quantità di Energia Ej, detta
energia di ionizzazione, per rompere il debole legame che lega l’elettrone in eccesso, al suo
atomo ed eccitarlo dal livello localizzato originale, alla banda di conduzione.
Impurezze pentavalenti si chiamano donatori ed i livelli loro associati si chiamano livelli
donatori.
Donatori ionizzati
sono ioni positivi
Accettori ionizzati
sono ioni negativi
Banda di conduzione
EC
Banda di conduzione
EC
Ej
Neutri
ionizzati
Gap
EV
Neutri
ionizzati
Ej
EV
Banda di valenza
Figura 1. Livelli donatori ionizzati e neutri
Banda di valenza
Figura 2. Livelli donatori ionizzati e neutri
In un campione di silicio o germanio contaminato con impurezze trivalenti come boro, alluminio
o gallio, si crea invece la situazione descritta in figura 2:
¾ attorno all’atomo di impurità che ha sostituito l’atomo di semiconduttore, si forma un buco in
eccesso (lacuna) o un elettrone in difetto. Tale buco, o lacuna, in eccesso può venire sostituito
da un elettrone ed allontanato dalla sua posizione iniziale, partecipando alla conduzione.
Il fenomeno è perfettamente analogo a quello sopra descritto per i donatori; le impurezze
trivalenti si dicono accettori e la loro presenza comporta la formazione di livelli accettori
localizzati nel “gap” in prossimità della banda di valenza.
Un semiconduttore drogato con atomi donatori si dice di tipo n, poiché le impurità offrono un
contributo di cariche negative alla conduzione; viceversa un semiconduttore drogato con atomi
accettori è detto di tipo p,
L’energia di ionizzazione degli atomi trivalenti e pentavalenti nel silicio è così bassa che già a
300°K l’energia termica reticolare è sufficiente ad operare una quasi totale ionizzazione delle
impurità. Si assumerà pertanto, d’ora in poi, che i droganti accettori e donatori siano, in
condizioni normali, totalmente ionizzati alla temperatura ambiente.
Nel caso di completa ionizzazione dunque ND donatori per cm3 cedono ND elettroni
di conduzione per cm3 (n = ND), mentre NA accettori per cm3 cedono NA buchi o
lacune per cm3 (p = NA).
Se la concentrazione di droganti è molto elevata, tipicamente maggiore di 1018 −
1019 cm-3, allora la condizione di completa ionizzazione non è verificata alla
temperatura ambiente, ed il semiconduttore si dice degenere.
LA NEUTRALITÀ DI CARICA
La carica totale contenuta in ogni zona di un semiconduttore omogeneo è nulla in condizioni di
equilibrio. Questa condizione di neutralità di carica è il risultato della compensazione tra cariche
positive e negative che, in caso di completa ionizzazione può esprimersi nella forma seguente:
NA + n = ND + p
(1)
in cui il primo membro indica la concentrazione di cariche negative (NA ioni ed “n” elettroni)
mentre il secondo membro esprime la concentrazione di cariche positive (ND ioni e “p” buchi o
lacune).
La relazione (1) si semplifica nel caso, verificato normalmente per il silicio alla temperatura
2
ambiente, in cui sia ⏐ND − NA⏐>> ni; infatti, ricordando l’equazione di equilibrio, n·p = ni si
può scrivere:
2
ni
n = ND − N A + p ⇒ n = ND − N A +
n
e per un semiconduttore n, in cui sia ⏐ND − NA⏐>> ni, la relazione precedente assume la forma:
n = ND − NA
(2)
mentre per un semiconduttore p, in cui sia ⏐NA − ND⏐>> ni, si ha invece:
p = NA − ND
(3)
Quando in un semiconduttore sono presenti ND donatori ed NA accettori ionizzati, si ha un effetto
di compensazione definito dalle relazioni (2) e (3).
I semiconduttori usati in pratica, contengono sia donatori, sia accettori, e vengono suddivisi nei
seguenti tre tipi
Se ND > NA
Semiconduttori di tipo n
Se NA > ND
Semiconduttori di tipo p
Se ND = NA
Semiconduttori compensati o impropriamente intrinseci
Si dicono portatori maggioritari le cariche mobili presenti in maggior numero e portatori
minoritari le cariche mobili presenti in minoranza. Il teorema di equilibrio applicato alle relazioni
(2) e (3) permette di ricavare la concentrazione di minoritari in funzione di quella dei maggioritari:
in un semiconduttore p:
2
p = N A − ND
n
⇒ i = N A − ND
n
2
ni
⇒ n=
N A − ND
in un semiconduttore n:
2
n = ND − N A
n
⇒ i = ND − N A
p
2
ni
⇒ p=
ND − N A
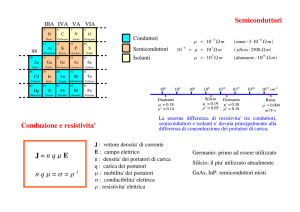
LA CONDUCIBILITÀ ELETTRICA
Le cariche mobili nei solidi sono soggette ad un moto disordinato di agitazione termica, con una
velocità dell’ordine di 107 cm·sec-1 alla temperatura ambiente. Durante questo moto le particelle
subiscono continue collisioni contro gli atomi del reticolo compiendo deviazioni in ogni direzione:
il risultato è quello di una velocità effettiva nulla.
Sotto l’influenza di un campo elettrico Ε la velocità Vth di agitazione termica si compone con la
velocità di spostamento dovuta all’azione del campo, col risultato di uno spostamento effettivo non
nullo nella direzione del campo elettrico. Il risultato è, quindi, espresso da una velocità di deriva vd,
che risulta essere proporzionale al campo Ε secondo la relazione seguente:
vd = µe·Ε
[m·sec-1]
in cui la costante di proporzionalità “µe” è chiamata mobilità degli elettroni e risulta definita dalla
relazione:
2
⎡ m ⋅ sec −1
m ⎤
⎢
⎥
=
−1
⋅
V
sec
⎢⎣ V ⋅ m
⎥⎦
v
µe = d
Ε
a) Densità di Corrente
N elettroni sono distribuiti uniformemente all’interno di un conduttore di lunghezza L e sezione
normale A. Un elettrone, sotto l’influenza di un “campo
N elettroni elettrico” Ε si sposta di un tratto di lunghezza L (metri) in un
tempo T (secondi) e questo avviene per effetto di una
velocità di deriva vd data dalla relazione:
vd = L T
L
La corrente I è, per definizione, la carica totale che attraversa
ogni
sezione del conduttore nell’unità di tempo ed è data dal
Sezione normale A
prodotto della carica elettrica di ogni portatore per il numero
di portatori che attraversano la sezione A in ogni secondo. Ciò premesso, si ha
I =q
N
N L qN
=q ⋅ =
⋅ vd
T
T L
L
[ Ampere]
La densità di corrente J, è la corrente per unità di area, ovvero J = I/A [A/m2]. Sostituendo, si
ottiene:
J=
I qN
N
1
=
⋅ vd ⋅ = q ⋅ vd ⋅
A L
A
A⋅ L
è evidente che il prodotto A·L è il volume contenente gli N elettroni. La concentrazione volumetrica
degli elettroni, o semplicemente la concentrazione degli elettroni è data da:
−3
numero elettroni
N
n=
volume
=
A⋅ L
[m ]
L’espressione della densità di corrente assume, allora, la forma seguente:
J=
I
N
= q ⋅ vd ⋅
= q ⋅ n ⋅ vd = δ C ⋅ vd
A
A⋅ L
2
[A/ m ]
in cui δC = q·n è la densità di volume di carica espressa in Coulomb per metro cubo (C/m3).
La relazione ottenuta è indipendente dalla forma del conduttore. Ricordando, inoltre, che la velocità
vd è proporzionale al campo elettrico Ε tramite la mobilità µn degli elettroni, tramite la relazione
già ricordata: vd = µn·Ε. Pertanto, in riferimento alla densità di corrente J, si ottiene:
2
J = q ⋅ n ⋅ vd = q ⋅ n ⋅ µ n ⋅ E = σ ⋅ E [ A / m ]
in cui: σ = q·n·µn è la conducibilità elettrica del materiale ed è espressa in (Ω·m)-1 oppure in
(mho·m-1). Infatti la conducibilità elettrica è definita, dalla prima legge di Ohm, come coefficiente
di proporzionalità tra densità di corrente J ed intensità del campo elettrico Ε.
Ricordando che il campo elettrico Ε è il gradiente del potenziale elettrico V del campo, allora la
relazione E·L = V definisce la tensione o differenza di potenziale applicata al conduttore. Si
ottiene così la scrittura di seguito riportata, nota come legge di Ohm:
I = J ⋅ A = σ ⋅ E ⋅ A = Aσ ⋅ E
L Aσ
V
=
⋅V =
L
L
R
in cui si definisce resistenza elettrica R del conduttore la grandezza individuata dalla relazione:
R=
1 L
L
L
= ⋅ =ρ
Aσ σ A
A
[Ω]
La grandezza fisica ρ = 1/σ, inverso della conducibilità elettrica definisce la resistività elettrica
del materiale conduttore.
b) Conducibilità e Resistività di un semiconduttore.
Nel caso di un materiale semiconduttore con concentrazione n di elettroni e p di buchi o lacune, la
conducibilità σ sarà data dalla somma dei contributi relativi alla conducibilità dei singoli portatori,
si ottiene, cioè, la relazione:
−1
σ = q ⋅ n ⋅ µ n + q ⋅ p ⋅ µ p [mho·cm ]
in cui µn e µp sono, rispettivamente, le mobilità degli elettroni e dei buchi o lacune. Si dimostra
che la mobilità è inversamente proporzionale alla massa efficace di una particella; nel silicio, a
causa delle diverse masse efficaci, la mobilità degli elettroni risulta circa tre volte maggiore della
mobilità delle lacune.
Alla luce di quanto sopra affermato, si evince che la resistività di un semiconduttore è espressa dalla
relazione seguente:
2
ρ=
1
σ
=
1
1
=
qµ n n + qµ p p q ⋅ ( µ n n + µ p p )
[
Ω⋅m
= Ω ⋅ m]
m
Ponendo n = p =ni nella relazione precedente, si ottiene l’espressione della resistività intrinseca
ρi. Nel caso del germanio e del silicio, alla temperatura ambiente di 300°K, ricordando che:
ni = 1,45·1010 cm− 3
ni = 2,40·1013 cm− 3
per il silicio ( Si )
per il germanio ( Ge )
si ottengono i valori seguenti di resistività:
ρi.= 47 Ω·cm
ρi.= 214.000 Ω·cm
per il Germanio
per il Silicio
Si nota che la resistività intrinseca ρi del silicio è molto maggiore essendo ni molto maggiore nel
germanio.
Introducendo le espressioni che forniscono le concentrazioni dei portatori per i semiconduttori
drogati in condizione di completa ionizzazione, si ricavano le seguenti espressioni per la resistività:
ρn =
ρp =
1
qµ n ( N D − N A )
1
qµ p ( N A − N D )
Per semiconduttori di tipo “n”
Per semiconduttori di tipo “p”
Le espressioni, ora ricavate, descrivono con buona approssimazione la dipendenza sperimentale
della resistività dalla concentrazione efficace di droganti, quale appare nel grafico di J. C. IRVIN.
che è riportato in figura 3. La resistività dipende dalla temperatura attraverso i parametri mobilità e
concentrazione di portatori; la resistività del silicio si può, in prima approssimazione, considerare
costante entro un ampio campo di temperatura attorno alla temperatura ambiente. Essa cresce
invece rapidamente alle bassissime temperature e decresce alle temperature a cui il silicio diventa
intrinseco.
La figura 3 riporta, in funzione della concentrazione totale di droganti, la mobilità dei buchi o
lacune e degli elettroni nel silicio, alla temperatura ambiente, ricavata da misure sperimentali
secondo E. M. CONWELL.
Figura - 3
La figura 4 mostra l’andamento della resistività del silicio, alla temperatura ambiente, in funzione
della concentrazione delle impurità, di tipo n e di tipo p, così come segnalato nella pubblicazione
di J.C. IRVIN.
Figura - 4