Percorsi logici

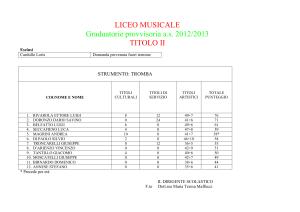
Percorsi logici
Prima lezione: Gli insiemi
A cura di Luigi Boscaino
Prima provocazione
Alunno:
Un giovane ha davanti a se sei maglie diverse per colore e
modello ma tutte della sua taglia. Quante possibili scelte può
fare il giovane con le sei maglie? (Considerare anche la
possibilità che non ne acquisti)
Risposta:
Attività di laboratorio
Percorsi logici a cura di Luigi Boscaino
Seconda provocazione
Alunno:
I soci di un club sportivo praticano almeno uno dei tre sport:
basket, nuoto, tennis. 21 giocano a basket, 23 a tennis, 19
praticano nuoto. 9 praticano basket e tennis, 7 basket e
nuoto, 8 tennis e nuoto. 3 di questi praticano tutti gli sport.
Sapendo che ogni mese il club incassa 2730 €, qual è la quota
mensile per ogni socio?
Risposta:
Attività di laboratorio
Percorsi logici a cura di Luigi Boscaino
Logica matematica
è il nome assegnato da Giuseppe Peano
a quella che era nota anche come logica
simbolica. In buona sostanza è ancora
la logica formale di Aristotele, ma viene
riconsiderata come branca dell'algebra
PEANO GIUSEPPE (1858-1932)
astratta e della combinatoria.
filosofo greco (384-322 a.C.)
Percorsi logici a cura di Luigi Boscaino
Le aree principali della logica matematica
Includono:
la teoria degli insiemi,
la teoria dei modelli,
la teoria della dimostrazione,
la teoria della ricorsione.
Percorsi logici a cura di Luigi Boscaino
Teoria egli insiemi
possiede molte sovrapposizioni con
l'informatica, fin dai lavori dei
pionieri di questa disciplina, come
2 nov 1815 - 8 dic 1864
George Boole e Alan Turing, i quali
erano matematici e logici.
23 giugno 1912-7 giugno 1954
Percorsi logici a cura di Luigi Boscaino
Teoria ingenua degli insiemi (Cantor)
Il concetto di insieme è alla base delle
scienze (Logica matematica, Matematica,
Informatica, Biologia, ecc.)
Come definiresti un Insieme?
Georg Cantor, 1845 - 1918
Percorsi logici a cura di Luigi Boscaino
Strano ma vero!
Tutto l'intero edificio della matematica si
basa sul concetto di insieme.
Cos'è un insieme? E' quasi incredibile, ma il
concetto di insieme non è definibile. Tutta
la matematica,
e quindi la scienza, si basa su un concetto
indefinibile !!!
Ma non è così anche per la geometria
euclidea?
Percorsi logici a cura di Luigi Boscaino
Proviamo con dei sinonimi
Il concetto di insieme è innato (primitivo),
solamente
intuibile ma non definibile.
Al massimo possiamo definire dei sinonimi:
aggregato, classe, collezione ecc.
Un contenitore ideale di cui è ben definito il
contenuto (Gigi Boscaino)
Percorsi logici a cura di Luigi Boscaino
Prendiamo spunto dai testi




Un insieme è una collezione distinguibile di oggetti, detti
elementi dell'insieme.
Un insieme è una collezione di oggetti ben definiti. Tali
oggetti si chiamano elementi dell'insieme.
Penseremo un insieme come una "collezione" di oggetti (in
generale facente parte di un fissato universo di discorso)
Intuitivamente con il termine insieme si indica una
collezione di oggetti chiamati elementi dell'insieme. In
molte esposizioni il concetto di insieme è considerato
primitivo ed intuitivo. (Fonte: WikipediA).
Percorsi logici a cura di Luigi Boscaino
Vediamo se è chiaro il concetto
Quali, tra quelli elencati, sono insiemi?

I fiumi italiani

Le donne giovani

Gli alunni della classe III A dell’IC di Torrecuso

I cani bassotti

Gli attori italiani più bravi

Gli stati d’America
Percorsi logici a cura di Luigi Boscaino
Modalità rappresentative

Per elencazione
A={0,1,2,3,4,5}

V={a,e,i,o,u}
Per caratteristica
A={numeri naturali <6}

Grafica
V={vocali}
A
1
3
0
4
5
V
u
a
2
o
Percorsi logici a cura di Luigi Boscaino
i
e
Esempio

Per elencazione
A={p, a}

Per caratteristica
A={lettere della parola “pappa”}

Grafica
A
a
p
Percorsi logici a cura di Luigi Boscaino
Sottoinsieme
Se tutti gli elementi di un insieme A sono
presenti in un altro insieme B allora A si dice
sottoinsieme di B
Percorsi logici a cura di Luigi Boscaino
Le operazioni insiemistiche

Insieme delle parti

Intersezione

Unione

Differenza

Prodotto cartesiano
Intersezione, unione e differenza le
affrontiamo in classe!
Percorsi logici a cura di Luigi Boscaino
Insieme delle parti
L’insieme delle parti risolve tutti i
problemi di scelta binaria di tipo (si/no o
vero/falso).
Se ho un vassoio con tre dolci, in quanti
modi posso scegliere quanti e quali dolci
prendere?
Percorsi logici a cura di Luigi Boscaino
Insieme delle parti
Si spazia dalla volontà di non mangiare
alcun dolce all’ingordigia di mangiarli tutti.
Potrei non desiderare alcun dolce (insieme vuoto)
Percorsi logici a cura di Luigi Boscaino
Insieme delle parti
Dunque tutte le scelte si possono esprimere mediante l’insieme
di tutti i possibili sottoinsiemi:
{}
{
{
{
}{
} {
} {
}
} {
}
Percorsi logici a cura di Luigi Boscaino
}
Problemi di distribuzione
Problemi di distribuzione risolti con le rappresentazioni
insiemistiche di Eulero-Venn
Percorsi logici a cura di Luigi Boscaino
Soluzione del problema 1 proposto all’inizio
Tutti
praticano uno sport
21 giocano a basket
23 giocano a tennis
19 praticano il nuoto
8 praticano nuoto e tennis
9 giocano a basket e tennis
7 basket e nuoto
Solo 3 praticano tutti gli sport
Modello matematico
Basket
Nuoto
4
8
I soci del club sono 42.
2730/42 = 65 €
Percorsi logici a cura di Luigi Boscaino
6
3
9
Tennis
7
5
Ora tocca a voi ….
Un gruppo di 50 studenti del Liceo Scientifico di Foglianise viene
intervistato in riferimento agli esami per il conseguimento della
Patente Europea del computer alla fine del primo anno
scolastico. Alle domande mirate cui gli intervistati vengono
sottoposti si ottiene l’esito seguente:







3 studenti hanno superato tutte le prove
13 hanno superato la seconda prova
5 studenti hanno superato la prima e la seconda
9 hanno superato la seconda e la terza
ben 30 studenti sostengono di aver superato la prima e la terza
36 studenti sostengono di aver superato la terza prova
infine 6 superano esclusivamente la prima.
Si desidera conoscere il numero dei candidati che ha superato
solo la terza prova e quanti studenti non hanno ancora superato
prove d’esame.
Percorsi logici a cura di Luigi Boscaino
Soluzione
•
•
•
•
•
•
•
3 studenti hanno superato tutte le prove
13 hanno superato la seconda prova
5 studenti hanno superato la prima e la seconda
9 hanno superato la seconda e la terza
ben 30 studenti sostengono di aver superato la prima e la terza
36 studenti sostengono di aver superato la terza prova
infine 6 superano esclusivamente la prima.
I
II
6
2
2
3
27
6
Nessuna
0
III
Percorsi logici a cura di Luigi Boscaino
4
Fine attività
Grazie per
l’attenzione!
Percorsi logici a cura di Luigi Boscaino