Liceo Scientico Paritario Ven. A. Luzzago di Brescia.
Classe 5A - Anno Scolastico 2012/2013 - Prof. Simone Alghisi
1
Funzione inversa
Come abbiamo visto, una funzione f : A → B è una relazione che ad ogni x ∈ A associa un
unico y ∈ B . Ci chiediamo se è possibile invertire tale relazione, cioè se è possibile trovare una
funzione g : B → A che ad ogni elemento y ∈ B associ uno ed un solo elemento x ∈ A tale per
cui g(y) = g(f (x)) = x. Diciamo subito che in generale, la relazione inversa di una funzione
non è una funzione. Infatti, ssato y ∈ B potrebbe non esistere in A alcun elemento la cui
immagine mediante f coincida con y , oppure potrebbero esisterne più di uno. Una situazione
del genere si verica per la funzione y = sin x. Fissato ad esempio y = 2, non esiste alcun x tale
che sin x = 2. Fissato invece y = 12 , esistono inniti valori di x per cui sin x = 12 (essi sono della
forma x = π6 + 2kπ oppure x = 56 π + 2kπ ). Si deduce che la relazione inversa di una funzione f
è anch'essa una funzione solo nel caso in cui f sia una funzione biiettiva.
(1.1) Denizione Siano A, B ⊆ R ed f
: A → B una funzione biiettiva. Chiamiamo funzione
inversa di f la funzione g : B → A tale che ad ogni y ∈ B associa l'unico elemento x ∈ A tale
per cui g(y) = g(f (x)) = x.
La funzione inversa g denita nella precedente denizione la si indica con f −1 e, per quanto
si è detto, risulta
∀x ∈ A :
f −1 (f (x)) = x .
(1.2) Esempio La funzione
f (x) = 2x − 1 è biiettiva. Risolvendo l'equazione y = 2x − 1
y+1
y+1
rispetto ad x, si ottiene x =
. La funzione inversa è quindi f −1 (y) =
.
2
2
(1.3) Osservazione Dal fatto che solo le applicazioni biiettive ammettono inversa sembrerebbe
che la funzione inversa si possa denire solo per una ristretta classe di funzioni. In realtà non
è proprio così. Data una funzione f : A → B possiamo cercare un sottoinsieme A0 di A ed un
sottoinsieme B 0 di B tali per cui la funzione f : A0 → B 0 sia biiettiva. In tal modo, restringendo
la funzione f al dominio A0 si può denire la funzione inversa f −1 che avrà come dominio B 0 .
(1.4) Esempio La funzione
f (x) = x2 è tale che dom (f ) =] − ∞; +∞[ e come codominio
[0; +∞[. La funzione non è biiettiva. Infatti, ssato y ∈ [0; +∞[, l'equazione y = x2 ammette
√
due valori distinti x = ± y . Se però restringiamo il dominio della funzione all'insieme R+ , la
√
funzione f diventa biiettiva ed ammette la funzione inversa f −1 (y) = y .
1
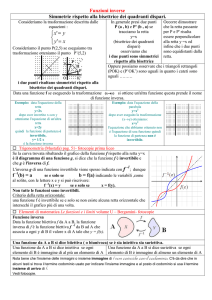
L'invertibilità di una funzione biiettiva f possiede un notevole risvolto sotto l'aspetto geometrico. Siano γ il graco della funzione y = f (x) e γ 0 il graco della funzione inversa. Nel piano
cartesiano xOy il graco della funzione inversa x = f −1 (y) coincide con quello della funzione
y = f (x). Se però si desidera avere la nuova x come variabile indipendente sulle ascisse allora
occorre scambiare il ruolo delle due coordinate. Invertendo l'ascissa con l'ordinata si ottiene
un graco simmetrico di quello originario rispetto alla bisettrice del primo e terzo quadrante.
Quindi, se γ è il graco della funzione biiettiva y = f (x), il graco γ 0 della funzione inversa
y = f −1 (x) (in cui x ed y sono state scambiate) non è altro che il simmetrico di γ rispetto alla
retta y = x.
Se la funzione f è invertibile, il dominio della funzione inversa coincide con il codominio della
funzione f . Il codominio della funzione inversa coincide con il dominio della funzione f .
(1.5) Esercizio Determinare, se esiste, la funzione inversa della funzione f (x) = e−x + 1.
Soluzione. Il dominio della funzione è dom (f ) = R. Risolvendo rispetto a x l'equazione y = f (x)
si ha
y = e−x + 1 ⇒ e−x = y − 1 ⇒ x = − log(y − 1) .
Avendo trovato una unica soluzione, la funzione f è invertibile. Inoltre il codominio di f coincide
con il dominio di f −1 che è
dom f −1 = {y ∈ R : y − 1 > 0} =]1; +∞[ .
Quindi il codominio di f è l'insieme ]1; +∞[. Si noti che la funzione è limitata inferiormente ma
superiormente illimitata.
(1.6) Esercizio Si consideri la funzione f
: R → R denita da
f (x) = y =
2x2 + 1
.
x2 + 1
Dire se la funzione data è invertibile e si determini la sua inversa f −1 . Determinare dom f −1
e si dica se f è limitata.
Soluzione. Anzitutto Df = dom (f ) = R. Risolvendo rispetto a y l'equazione y = f (x) si ha
r
2x2 + 1
1−y
2
y= 2
⇒ x (y − 2) = 1 − y ⇒ x = ±
.
x +1
y−2
Dal fatto che non si trova un'unica soluzione x dell'equazione y = f (x) si può aermare che la
funzione non è invertibile in R. Esistono tuttavia due funzioni inverse:
f
−1
r
(y) =
1−y
y−2
e
f
2
−1
r
1−y
(y) = −
,
y−2
ciascuna in un'opportuna restrizione del dominio Df . Tuttavia dom f −1 = [1; 2[. Questo
intervallo è anche il codominio della funzione f : Cf = [1; 2[. Dal fatto che Cf è limitato, segue
che la funzione f è limitata.
(1.7) Esercizio Si consideri la funzione f
: R → R denita da f (x) = 2 + 2 sin(5x). Si dica se
f è invertibile e si trovi (se esiste) la funzione f −1 . Determinare il codominio della funzione f
e dire se f è limitata.
Soluzione. Risolvendo l'equazione y = f (x) si ha
sin(5x) =
y−2
.
2
Sappiamo che la funzione seno non è biunivoca in R, ma lo è nell'intervallo I = [−π/2; π/2].
Possiamo quindi invertire la funzione sin(5x) quando −π/2 ≤ 5x ≤ π/2, cioè x ∈ [−π/10; π/10].
In questo caso otteniamo
5x = arcsin
y−2
2
Inoltre
dom f
−1
=
⇒ f
−1
1
(y) = arcsin
5
y−2
≤1
y ∈ R : −1 ≤
2
y−2
2
.
= [0; 4] .
Segue che il codominio della funzione y = f (x) è Cf = [0; 4] e quindi la funzione f è limitata
poichè il suo codominio è limitato.
Esercizi
x2 − 2
. Si dica se è invertibile ed eventualmente si determini
x
f −1 . Determinare il codominio della funzione y = f (x).
1. Si consideri la funzione
2. Si consideri la funzione
y =
g(x) = x2 + 1 + 2x.
Dire se g è invertibile ed eventualmente
determinarne l'inversa g −1 . Si trovi il codominio Cg .
3. Determinare la funzione inversa di y = log5 (x+1). Determinare inoltre dom (f ) e il codominio
di f .
3