Campo elettrico in un conduttore
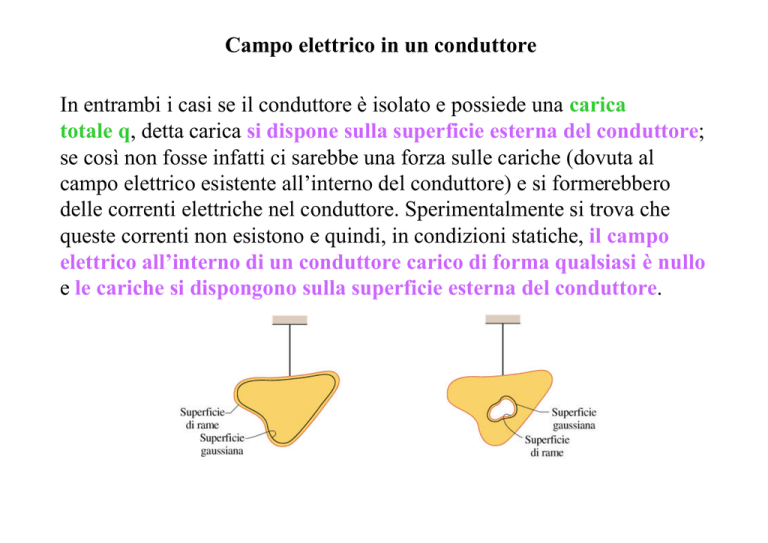
In entrambi i casi se il conduttore è isolato e possiede una carica
totale q, detta carica si dispone sulla superficie esterna del conduttore;
se così non fosse infatti ci sarebbe una forza sulle cariche (dovuta al
campo elettrico esistente all’interno del conduttore) e si formerebbero
delle correnti elettriche nel conduttore. Sperimentalmente si trova che
queste correnti non esistono e quindi, in condizioni statiche, il campo
elettrico all’interno di un conduttore carico di forma qualsiasi è nullo
e le cariche si dispongono sulla superficie esterna del conduttore.
Campo elettrico di una distribuzione sferica di cariche
Prendiamo una sfera di raggio a con carica q
il campo, per questioni di simmetria deve
essere radiale.
Consideriamo ora una superficie gaussiana di
raggio r concentrica con la prima, abbiamo
r r
Φ Er = ∫ E ⋅ u n dS = E ∫ dS = E 4πr 2
S
S
Applichiamo Gauss e d esaminiamo le possibilità al variare di r
r > a la carica q è tutta contenuta nella superficie gaussiana di raggio r
(
)
E 4πr 2 =
q
q
⇒E=
ε0
4πε 0 r 2
È come se la carica fosse tutta
concentrata nel centro della sfera
r<a
•Se la carica è superficiale ⇒ E = 0
•Se la carica è distribuita uniformemente in tutto il volume della sfera
q’ è la carica contenuta all’interno della superficie gaussiana e vale
q' =
q
4 3
q
πr = 3 r 3
4 3 3
a
πa
3
Quindi
3
qr
q
E (4πr 3 ) =
⇒
E
=
r
3
3
ε0 a
4πε0 a
Il campo elettrico dentro ad una sfera isolante uniformemente carica
varia proporzionalmente ad r
Infine resta da esaminare cosa succede sulla superficie della sfera
r=a
E− =
q a
q 1
=
venendo dall' interno
3
2
4πε 0 a
4πε 0 a
q 1
E+ =
4πε 0 a 2
venendo dall' esterno
I due alori E+ ed E- coincidono quindi il campo E è continuo
r=0⇒ E=0
E
a
r
Campo elettrico generato da una distribuzione cilindrica di carica
di lunghezze infinita
Consideriamo una distribuzione di carica per unità
di lunghezza λ distribuita uniformemente su un tratto
cilindrico di altezza h e tale che q = λ h; sia a il
raggio del cilindro. Il campo elettrico ha direzione
radiale per questioni di simmetria e certamente
dipenderà dalla distanza r dall’asse del cilindro.
Considero una superficie cilindrica coassiale alla
superficie carica e con raggio r, il flusso attraverso
detta superficie vale sempre
Φ Er = Φ Er (B1 ) + Φ Er (B2 ) + Φ Er (sup. lat.) = Φ Er (sup. lat.)
r r
Φ Er (sup. lat.) = ∫ E ⋅ un dS =E 2πrh
S
Anche in questo caso dobbiamo distinguere vari casi
r > a la carica q è tutta contenuta nella superficie gaussiana di raggio r
λh
λ 1
2πrhE =
⇒E=
ε0
2πε 0 r
Come nel caso del filo infinito con
carica uniforme
r< a
•Se la carica è superficiale ⇒ E = 0
•Se la carica è distribuita uniformemente in tutto il volume del cilindro
q’ è la carica contenuta all’interno della superficie gaussiana e vale
πr 2 h
r2
r2
q ' = q 2 = q 2 = λh 2
πa h
a
a
λhr 2
λ
2πrhE =
⇒E=
r
2
2
ε0a
2πε 0 a
Il campo elettrico dentro ad un cilindro isolante uniformemente carico
varia proporzionalmente ad r (come per la sfera)
Infine resta da esaminare cosa succede sulla superficie del cilindro
r=a
E− =
λ a
λ 1
=
venendo dall' interno
2
2πε 0 a
2πε 0 a
λ 1
E+ =
2πε 0 a
venendo dall' esterno
I due limiti coincidono quindi il campo E è continuo
r=0⇒ E=0
E
a
r
Legge di Gauss in forma differenziale
La parete ABCD ha area dS = dxdz e il flusso
z
del campo elettrico attraverso di essa vale
C’ C E
D’
D
Φ Er ( ABCD ) = EdS cos ϑ = (E cos ϑ )dxdz = E y dxdz
Ey
B’ B
θ
y
dx
Attraverso A’B’C’D’ abbiamo un flusso negativo
A’ dy A
x
Φ Er ( A' B' C' D') = −Ey' dxdz
'
Attraverso la superficie del cubo in direzione y il flusso vale
(
) (
)
Φ Er ( y ) = E y dxdz + − E 'y dxdz = E y − E y' dxdz
Se ora ricordiamo che AA’ = dy è infinitesimo, abbiamo che anche la
differenza Ey – E’y è molto piccola, quindi
E y − E y' = dE y =
con
∂E y
∂y
∂E y
∂y
dy
r
rapiditàdi variazionedella componente y di E
Quindi il flusso totale in direzione y vale
∂E y
∂E y
dy dxdz =
dV
∂y
∂y
Attraverso tutto il volume abbiamo
∂E y
∂E x
∂E
Φ =
dV +
dV + z dV =
∂x
∂y
∂z
r
E
∂E x ∂E y ∂Ez
dq
dV =
=
+
+
∂y
∂z
ε0
∂x
Ricordando ora che dq = ρ dV, otteniamo
∂E x ∂E y ∂Ez ρ
+
+
=
∂x
∂y
∂z ε 0
r ρ
divE =
ε0
Relazione locale tra campo elettrico e distribuzione di carica
Il potenziale elettrico e l’energia potenziale
Forza elettrica è centrale ⇒ conservativa ⇒ energia potenziale elettrica
Definiamo il potenziale elettrico in un punto come l’energia potenziale
posseduta da una carica unitaria posta in quel punto
U
V=
q
U = qV
[V ] = volt
V = m2 kgs − 2C −1
Il potenziale è una caratteristica del campo e non della carica
Il potenziale, come U, è definito a meno di una costante arbitraria:
poniamo V = 0 per r = ∞
q si muove da A verso B lungo la curva e
VB
attraversa una regione in cui c’è campo
E
B
elettrico E
ds ES
U A − U B = q(VA − VB )
VA
U A − U B = −∆U = LA→B lavoro fatto sulla carica
A
Pertanto troviamo
LA→ B = q (V A − VB )
differenza di potenziale elettrico
r r B r r
= ∫ F ⋅ dr = ∫ qE ⋅ dr
B
LA→B
A
Possiamo anche definire il potenziale
come il lavoro fatto dal campo elettrico
per portare la carica di prova dall’infinito
al punto in cui si misura V, V = (-L∞ /q)
A
r r
∫ E ⋅ dr = VA − VB
B
A
Lungo un percorso chiuso, dato che il campo è conservativo, abbiamo
r r
∫ E ⋅ dr = 0
In generale, lungo un percorso qualunque se ES è la componente del
campo lungo il percorso, si ha
B
∫ E ds = V
S
A
B
A
− VB = −(VB − V A ) = −∫ dV
A
Se A e B sono molto vicini possiamo scrivere
E S ds = − dV
Ex = −
ES = −
∂V
∂V
Ey = −
∂x
∂y
Quindi
∂V
∂s
Ez = −
∂V
∂z
r
E = − gradV
In questo modo posso calcolare V noto E e viceversa
Ad esempio consideriamo un campo elettrico uniforme (E = costante)
con unica componente lungo l’asse delle x
x
Edx = −dV
x
∫ Edx = −∫ dV
0
V = 0 per x = 0
0
V = -Ex
Notiamo che in questo caso il potenziale cresce nella direzione in cui il
campo elettrico decresce, ovvero che la direzione del campo elettrico è
quella in cui V decresce
Se mi sposto da x1 ad x2 ho
V1 = − Ex1
V2 = − Ex2
V2 − V1 = − E ( x2 − x1 )
E=−
V2 − V1 V1 − V2
=
d
d
d = (x 2 − x1 )
[E ] = Vm −1 = NC −1
Notiamo che
•se V1-V2 > 0 ⇒ E va da x1 a x2
•se V1-V2 < 0 ⇒ E va da x2 a x1
Consideriamo ora una carica puntiforme q sorgente del campo E
∂V
E=−
∂r
q
dV
=
−
4πε0 r 2
dr
q
4πε0
V=
∞
q>0
0
dr
∫0 r 2 = −V∫ dV
q 1
4πε0 r
V = 0 per r = ∞
V > o < 0 a seconda della carica
Il potenziale V è additivo, pertanto se ho più cariche, ottengo
q1
q2
qn
1
V=
+
+ ... +
=
4πε0 r1 4πε0 r2
4πε0 rn 4πε0
n
qi
∑
i =1 ri
Le superfici per cui è V = costante sono superfici equipotenziali, E è
sempre ⊥ ai punti di una superficie equipotenziale (il lavoro per
muoversi su una superficie equipotenziale è nullo)
Se E è uniforme, allora V = costante ⇒ x = costante ⇒ superfici
equipotenziali sono dei piani
Se E è generato da una carica puntiforme ⇒ superfici equipotenziali
sono delle sfere
Consideriamo il caso del filo di lunghezza infinita ed uniformemente
carico con distribuzione lineare di carica λ
r
E=
λ r r
ur E = - gradV
2πε 0 r
dV
λ 1
E =−
=
dr 2πε 0 r
λ
dr
− ∫ dV =
2πε 0 ∫ r
V =−
λ
ln r + C se C = 0 per r = 1 ⇒ V(1) = 0
2πε 0
Consideriamo ora l’energia totale di una particella di massa m e carica q
in una zona in cui è presente un campo elettrico E
1
ETOT = EK + U = mv 2 + qV
2
Dato che non ci sono forze dissipative, quando la particella si muove dalla
posizione 1 alla 2 abbiamo, per il principio di conservazione dell’energia
ETOT (1) = ETOT (2)
1 2
1
mv1 + qV1 = mv22 + qV2
2
2
1
1
∆EK = L1→ 2 = mv22 − mv12 L1→ 2 = q(V1 − V2 )
2
2
1 2 1 2
mv2 − mv1 = q(V1 − V2 )
2
2
12
Volt = variazione di potenziale elettrico che una carica di 1 C deve
effettuare per aumentare la propria energia di 1 J
q > 0 EK aumenta spostandosi verso V inferiori
q < 0 EK aumenta spostandosi verso V superiori
Se v1 = 0 e in 2 è V2 = 0
1 2
mv2 = qV1 ⇒ principiosu cui si basano gli acceleratori elettrostatici
2
1 eV = (1.6 · 10-19 C ) (1 V) = 1.6·10-19 J
Ee = mec2 = 8.1867 ·10-14 J = 0.511 MeV
Ep = mpc2 = 1.5032 ·10-10 J = 938.26 MeV
En = mnc2 = 1.5053 ·10-10 J = 939.55 MeV
Riconsideriamo ora il caso della sfera isolante con carica q e raggio R
a) carica superficiale uniforme σ
0≤r ≤R
E =0
r=R
ER =
r>R
q 1 σ R2
E=
=
2
4πε 0 r
ε0 r2
q 1
σ
=
4πε 0 R 2 ε 0
r2
V = VR = costante
σ
VR = R = ER R
ε0
q
V (r2 ) − V (r1 ) = − ∫ Edr =
4πε 0
r1
r2 → ∞
V (r2 ) → 0
q 1 σ R2
V (r ) =
=
4πε 0 r ε 0 r
1 1
−
r2 r1
b) carica volumetrica uniforme ρ
r=0
E =0
0<r<R
4
q(r) = ρ πr 3
q = ρV
3
q(r) 1
ρ r 3 ρr
E=
=
=
2
2
4πε 0 r
3ε 0 r
3ε 0
r=R
E = ER =
r>R
q 1
ρ R3
E=
=
2
4πε 0 r
3ε 0 r 2
q 1
ρR
=
4πε 0 R 2 3ε 0
Per il potenziale abbiamo
r >R
r =R
0<r< R
q 1 ρR 3 1
V=
=
4πε 0 r 3ε 0 r
q 1
ρR 2
V = VR =
= ER R =
4πε0 R
3ε 0
dV
=E
dr
VR
R
V(r)
r
- ∫ dV = ∫ Edr
ρr
ρ R
ρ 1 2 1 2
ρ
VR − V (r ) = − ∫
dr = −
rdr
=
−
R
−
r
=
−
(
R2 − r2 )
∫
3ε 0
3ε 0 r
3ε 0 2
2
6ε 0
r
R
ρ
ρR 2 ρR 2 ρr 2
2
2
V (r ) = VR +
(R − r ) = 3ε + 6ε − 6ε
6ε 0
0
0
0
1 ρR 2 ρr 2
V (r) =
−
2 ε0
6ε 0
r =0
ρR 2
V(0) =
= VMAX
2ε 0












