Terminologia e definizioni generali
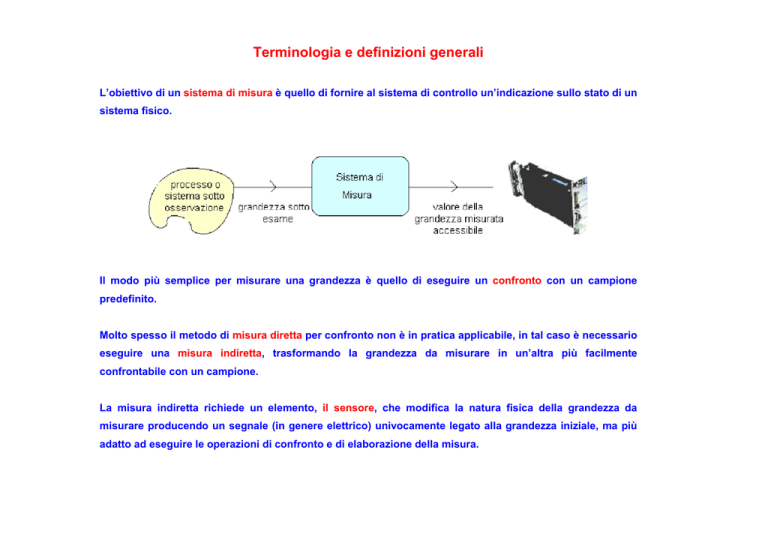
L’obiettivo di un sistema di misura è quello di fornire al sistema di controllo un’indicazione sullo stato di un
sistema fisico.
Il modo più semplice per misurare una grandezza è quello di eseguire un confronto con un campione
predefinito.
M lt spesso il metodo
Molto
t d di misura
i
diretta
di tt per confronto
f
t non è in
i pratica
ti applicabile,
li bil in
i tal
t l caso è necessario
i
eseguire una misura indiretta, trasformando la grandezza da misurare in un’altra più facilmente
confrontabile con un campione.
La misura indiretta richiede un elemento, il sensore, che modifica la natura fisica della grandezza da
misurare producendo un segnale (in genere elettrico) univocamente legato alla grandezza iniziale, ma più
adatto ad eseguire le operazioni di confronto e di elaborazione della misura.
Terminologia e definizioni generali
La definizione di sensore data dall’ International Electrotechnical Commission (IEC) è:
“L’ l
“L’elemento
t primario
i
i di una catena
t
di misura
i
che
h converte
t la
l variabile
i bil d’ingresso
d’i
in
i un segnale
l adatto
d tt alla
ll misura”
i
”
Terminologia e definizioni generali
La definizione di trasduttore data dall’ International Electrotechnical Commission (IEC) è:
“Dispositivo che accetta un’informazione nella forma di una variabile fisica (variabile d’ingresso) e la trasforma in una
variabile d’uscita della stessa o di diversa natura in accordo con una legge nota”
Il trasduttore quindi può essere identificato con l’intera catena di misura, mentre il sensore è il primo elemento della
stessa catena di misura.
In molti casi la distinzione tra sensore e trasduttore non è così netta e molto spesso nella letteratura tecnica e nella
pratica comune i due termini sono utilizzati come sinonimi.
sinonimi
Terminologia e definizioni generali
Le grandezze fisiche oggetto di misura da parte dei trasduttori possono essere classificate in:
grandezze continue, che possono assumere valori continui all’interno di un certo intervallo (es.
temperatura di un utensile,
utensile velocità di rotazione di un motore
motore, ecc
ecc...).
)
grandezze discrete, che assumono un insieme discreto di valori (es. verso di rotazione di un motore,
numero di pezzi lavorati al minuto, ecc...).
Le informazioni associate alle grandezze fisiche sono dette segnali.
•
•
le grandezze continue sono descritte da segnali analogici.
[
li logici,
l i i nell caso sii abbiano
bbi
due
d
valori
l i
segnali
ammissibili
le grandezze discrete sono descritte da:
segnali codificati, se il numero di valori ammissibili è
superiore a due
Terminologia e definizioni generali
Il principio di funzionamento di un sensore è basato su una legge fisica nota che regola la relazione tra la
grandezza fisica da misurare e una grandezza elettrica d’uscita.
Un esempio di sensore è la termoresistenza (sensore di temperatura).
La resistività si modifica al variare della temperatura.
ρ
R=
ρ = ρ 1 (1 + αΔθ )
ρ
1
ϑc
Vm
l
=ρ
I ref
S
ϑ1
ϑ
Δθ =
ρ − ρ 1 R − R1
=
αρ 1
αR1
Per poter acquisire il segnale occorre fornire una corrente (o una tensione) e misurare poi la tensione
(corrente) generata.
Classificazione dei sensori
•
In base alla grandezza da misurare
•
In base al principio fisico utilizzato
Classificazione dei sensori
•
In base alle caratteristiche energetiche:
♦Sensori attivi: convertono direttamente l’energia dell’ ingresso in energia di uscita, senza
l’ ausilio di sorgenti esterne.
♦Sensori passivi: richiedono energia dall’ esterno (eccitazione) per la conversione.
Classificazione dei sensori
•
In base al tipo di segnale che forniscono:
•
sensori analogici: forniscono un segnale elettrico continuo a risoluzione infinita, l’uscita cioè può
assumere infiniti valori all’interno di un dato intervallo.
•
sensori digitali: forniscono una informazione di tipo numerico con risoluzione finita, l’uscita cioè può
assumere solo un numero finito di valori all’interno di un dato intervallo.
•
Sensori logici: hanno una uscita di tipo booleano, codificata usualmente con la cifra “1”
(vero, presenza) e “0” (falso, assenza).
•
Sensori codificati: hanno un’uscita numerica codificata in una stringa di bits.
Errori di acquisizione del segnale
L’
L’operazione
i
di acquisizione
i i i
del
d l segnale
l da
d parte
t di un trasduttore
t
d tt
è inevitabilmente
i
it bil
t affetta
ff tt da
d errorii
dovuti alla non idealità del componente e della catena di amplificazione ed acquisizione del segnale
stesso.
Si intendono per errori le cause che fanno si che l’indicazione della misura non corrisponda esattamente
alla grandezza da misurare.
Gli errori possono essere classificati come:
•
Errori sistematici - Un errore è sistematico se, fissate le condizioni sperimentali, in grandezza e
segno ha la stessa influenza sul risultato della misura.
•
Errori casuali - Errori la cui influenza sulla misura può cambiare in grandezza e segno se si
ripete la procedura di misurazione
misurazione. (Le condizioni ambientali sono sorgenti di errori casuali se
non vengono monitorate o se non si conosce la loro influenza sulla grandezza da misurare,
diversamente possono essere sorgenti di errore sistematico).
•
Errori grossolani - Errori che riguardano l’operatore o guasti dello strumento.
Caratteristiche metrologiche dei trasduttori.
Le caratteristiche di funzionamento dei trasduttori possono essere raggruppate in tre categorie.
•
Caratteristiche statiche - Si riferiscono a condizioni di funzionamento in cui viene variata molto lentamente la
variabile di ingresso del sensore, registrando la corrispondente variabile di uscita.
•
Caratteristiche dinamiche - Se la variabile di ingresso varia velocemente l’uscita può evidenziare
un’attenuazione rispetto alla caratteristica statica ed un ritardo. La caratteristica dinamica del trasduttore
pone un limite alla banda passante di tutto il sistema di controllo.
•
Specifiche statistiche ed ambientali - E’ praticamente impossibile realizzare un dispositivo che operi per un
tempo illimitato
illimitato, mantenendo costanti le proprie caratteristiche e il cui funzionamento non venga influenzato
da altre grandezze fisiche oltre quella misurata. Ad esempio la temperatura o l’umidità.
Specifiche statiche
Range di ingresso e d’uscita
Linearità
Errore di offset
Errore di soglia
Errore di guadagno
Errore di isteresi
Risoluzione
Sensibilità
Precisione
Accuratezza
Deriva
Caratteristica statica
La caratteristica statica di un trasduttore è definita da una funzione del tipo:
dove il segnale X rappresenta il segnale di ingresso e Y il segnale di uscita dal trasduttore.
La caratteristica è definita su di un intervallo finito chiamato campo di ingresso avente estremi Xm e
XM ed ha valori sul campo di uscita (output range o span) con estremi Ym e YM.
Si definiscono:
Range d’ingresso: Xs = XM - Xm
Range d’uscita:
Ys = YM - Ym
E’ necessario selezionare opportunamente i range d’ingresso
E
d ingresso e d’uscita
d uscita del trasduttore in funzione
rispettivamente dei valori assunti dalla grandezza da misurare e delle specifiche del sistema di
calcolo, per assicurare livelli ottimali di sensibilità e risoluzione ed evitare danni al trasduttore.
Caratteristica statica
La caratteristica statica di un sensore deve avere idealmente un andamento lineare. La costante di
proporzionalità fra valori di ingresso e di uscita viene chiamata guadagno (K) del trasduttore.
I trasduttori commerciali hanno una caratteristica statica reale che si differenzia da quella ideale a
causa di inevitabili imperfezioni costruttive. La qualità di un sensore si misura in base a quanto la
caratteristica reale si scosta da quella ideale.
Linearità
La linearità di un trasduttore può essere definita in diversi modi, non del tutto equivalenti.
Secondo la definizione rigorosamente matematica, un sistema é lineare se la sua caratteristica
soddisfa le proprietà additiva ed omogenea, vale a dire se la sua caratteristica Y = f(X) soddisfa la
seguente eguaglianza:
Per un trasduttore lineare la relazione tra la g
grandezza
descrivibile attraverso una semplice relazione matematica:
essendo K il guadagno del trasduttore.
fisica misurata e il segnale
g
in uscita è
Errore di linearità
L’errore di linearità è la massima deviazione dell’uscita del trasduttore rispetto alla caratteristica
lineare che approssima al meglio la caratteristica reale
Errore di linearità
Tale caratteristica lineare viene normalmente ottenuta secondo il metodo dei minimi quadrati, cioè si
cerca quella retta r(X) che minimizzi la quantità:
Indicando con ΔY il massimo scostamento dalla caratteristica lineare, l’errore percentuale di non
linearità vale:
Errore di Offset
L’errore di Offset (o di fuori zero) è il valore d che assume l’uscita del trasduttore (Yo) quando la
grandezza da misurare è nulla.
Errore di Offset
La caratteristica di un trasduttore con offset non è lineare, anche se è definita tramite una retta, infatti,
se si considerano due grandezze fisiche in sequenza X1 e X2 , la lettura della grandezza pari alla
somma di X1 e X2 :
è differente rispetto alla somma delle letture del trasduttore:
Per rendere lineare la caratteristica occorre eliminare il termine di “offset” d dalla caratteristica del
trasduttore:
Errore di soglia
L’errore di soglia corrisponde al più basso livello di segnale rilevabile dal sensore. Esso non sempre
coincide con lo zero della grandezza da misurare.
Per rendere lineare la caratteristica occorre eliminare il termine di “soglia” s dalla caratteristica del
trasduttore:
Errore di guadagno
L’errore di guadagno è la differenza tra il guadagno della caratteristica ideale del trasduttore (K) e il
guadagno della retta (K1) che approssima al meglio la caratteristica reale del trasduttore.
L’errore di guadagno è solitamente espresso in percentuale:
Errore di isteresi
Il fenomeno dell’isteresi si manifesta nel caso in cui la caratteristica del trasduttore risulta differente
nella situazione in cui la grandezza da acquisire risulta crescente rispetto al caso in cui sia
decrescente.
L’errore di isteresi è la massima differenza tra le uscite del trasduttore a parità di grandezza in
ingresso, valutate in un primo caso per valori crescenti e in un secondo per valori decrescenti.
Campionamento e Quantizzazione
Il calcolatore di processo opera su dati numerici è quindi necessario trasformare il segnale analogico
da misurare in una sequenza di valori numerici. Ciò viene fatto automaticamente dai sensori digitali
codificati mentre è necessario utilizzare un sistema di conversione analogico/digitale nel caso di
sensori analogici.
Un segnale analogico ha la caratteristica di essere continuo nel tempo ed assumere valori continui
all’interno di un certo intervallo.
Campionamento e Quantizzazione
Il calcolatore di processo impiega un certo intervallo di tempo per elaborare i segnali di ingresso,
ingresso e
quindi non può seguire l’evolversi continuo del segnale analogico, ma dovrà acquisire campioni del
segnale analogico ad istanti discreti di tempo.
Questa operazione viene detta campionamento del segnale.
Campionamento e Quantizzazione
Il segnale campionato assume valori continui, e quindi teoricamente infiniti, mentre il calcolatore può
rappresentare un numero finito di valori in base alla massima dimensione di parola rappresentabile
dall’unità
dall
unità aritmetica.
aritmetica
Occorre eseguire una operazione di approssimazione del valore campionato al più vicino valore
rappresentabile dal calcolatore. Tale operazione viene detta quantizzazione del segnale.
Errore di Quantizzazione
L’informazione associata alla grandezza analogica campionata e quantizzata viene detta segnale
digitale.
•
L’operazione di campionamento non produce in via teorica un degrado dell’informazione
associata al segnale (se si rispettano le condizioni del teorema del campionamento),
•
L’operazione di quantizzazione comporta inevitabilmente l’introduzione di un errore sul
segnale acquisito.
Se YM e Ym sono rispettivamente il massimo ed il minimo valore assunto dal segnale Y in uscita dal
trasduttore, l’intervallo di valori Ys che l’uscita Y può assumere (output range o span), è dato da:
Rappresentando il segnale di uscita del trasduttore Y mediante una codifica binaria a N bits
(quantizzazione), ogni singolo bit corrisponde ad un valore detto LSB (o “bit meno significativo”) pari
a:
Errore di Quantizzazione
L’LSB corrisponde al valore minimo rappresentabile dalla codifica digitale, viene anche chiamato
quanto e rappresentato dal simbolo q.
A causa della quantizzazione,
quantizzazione tutti i valori di Y compresi all’interno di un LSB sono rappresentati da
una unica codifica digitale Yd, e quindi l’errore di quantizzazione è pari a:
Errore complessivo
Tutte le possibili sorgenti di errore vanno considerate nella valutazione dell’errore complessivo sul
segnale d’uscita del trasduttore:
L’errore sul segnale in uscita del trasduttore non è significativo se rimane inferiore all’errore di
quantizzazione, cioè se:
Risoluzione e Sensibilità
La risoluzione di un trasduttore è pari all’errore di quantizzazione e corrisponde alla più piccola
quantità che può essere misurata; ovvero alla minima variazione dell'ingresso che provoca
un'apprezzabile variazione in uscita.
L sensibilità
La
ibilità di un trasduttore
t d tt
è d
definita
fi it come la
l massima
i
variazione
i i
dell’uscita
d ll’
it rapportata
t t alla
ll
massima variazione dell’ingresso:
Occorre porre attenzione a non confondere la risoluzione e la sensibilità di un trasduttore.
La
definizione di sensibilità non tiene conto del segnale minimo o dalla minima variazione di segnale
misurabile, informazione che invece è contenuta nella definizione di risoluzione.
Precisione ed Accuratezza
Può accadere che ripetendo lo stesso esperimento più volte il sensore non fornisca l’identico
risultato.
La precisione di un trasduttore è una misura di quanto la sua uscita sia ripetibile su ripetuti
esperimenti.
La precisione di un sensore è indicata fornendo un intervallo di errore massimo (± errore), oppure una
percentuale di errore rispetto al campo di uscita:
dove eMAX rappresenta la variazione massima di lettura del trasduttore in corrispondenza dello stesso
valore della grandezza misurata.
Precisione ed Accuratezza
L’accuratezza è una misura di quanto l’uscita del trasduttore si scosta da quella che dovrebbe essere
l’uscita ideale, cioè quella uscita che avrebbe un trasduttore ideale che misurasse la stessa
grandezza di quello reale.
L’accuratezza viene espressa in percentuale rispetto al valore ideale:
Precisione ed Accuratezza
L’accuratezza non va confusa con la precisione: l’accuratezza ci fornisce un indice di quanto il
trasduttore dia una indicazione fedele al valore vero della variabile che si vuole misurare, la precisione
ci fornisce una misura di quanto l’uscita del sensore sia ripetibile.
La distinzione tra errori sistematici ed errori casuali si riflette sulla distinzione tra accuratezza e
precisione.
i i
L’accuratezza è influenzata da tutti gli errori,
La precisione è influenzata solo dagli errori casuali (quelli sistematici non contribuiscono infatti alla
variazione dei risultati).
Precisione ed Accuratezza
Preciso - Non accurato
Non preciso - Accurato
Preciso - Accurato
Non preciso - Non accurato
Deriva
Si definisce deriva la possibile variazione nel tempo della caratteristica statica di un sensore
(staratura).
Si può verificare sia una deriva di zero che una deriva di sensibilità. Nel primo caso si ha lo
spostamento verticale della caratteristica d’uscita, nel secondo cambia il coefficiente angolare.












