capitolo
2
L’insieme dei numeri naturali e l’insieme degli interi Congruenze. Classi resto
Congruenze modulo un intero
DEFINIZIONE Siano a e b due numeri interi relativi; fissato un intero m ≥ 2 si dice che
a è congruo a b modulo m se la differenza
a−b
è multipla di m, e si scrive:
a ≡ b (mod m)
In simboli, indicata con m la relazione di congruenza modulo m, si ha:
a m b
⇔
∃k ∈ a − b = km
Si tratta di una relazione di equivalenza (vedi cap. 1 par. 8); nell’esempio che segue ci limitiamo a verificarlo nel caso particolare m = 7.
sempio
1
Sia 7 la relazione tra gli elementi di così definita:
a 7 b
⇔
∃ k ∈ a − b = 7k
essendo k un intero positivo, negativo o nullo; tale relazione viene solitamente indicata con la
notazione
a ≡ b (mod 7)
che si legge “a è congruo a b modulo 7”, e significa che
a−b
è divisibile per 7
Per esempio:
18 è congruo a 11 modulo 7
infatti la differenza 18 – 11 = 7 è multiplo di 7; risulta ancora che
18 è congruo a 4 modulo 7
essendo 18 – 4 = 14 = 2 ⋅ 7 multiplo di 7.
Così, 3 è, per esempio, congruo ai numeri
24, – 32, – 4, 45 modulo 7
poiché sono multiple di 7 tutte le differenze:
3 – 24 = –21 = –3 ⋅ 7,
3 – (–32) = 35 = 5 ⋅ 7,
3 – (– 4) = 7,
3 – 45 = – 42 = – 6 ⋅ 7
Si vede subito che 7 è una relazione di equivalenza; infatti essa è:
a) riflessiva:
a ≡ a (mod 7)
in quanto
a − a = 0 ⋅ 7 (k = 0);
b) simmetrica:
a ≡ b (mod 7) ⇒ b ≡ a (mod 7)
in quanto
a − b = k 7 ⇒ b − a = (−k)7;
c) transitiva:
a ≡ b (mod 7) e b ≡ c (mod 7) ⇒ a ≡ c (mod 7)
in quanto, dalle relazioni
a − b = k 17
e
b − c = k 27
sommando membro a membro si ottiene:
a − c = (k 1 + k 2)7
1
ossia
a ≡ c (mod 7)
© 2010 RCS Libri S.p.A., ETAS - L. Lamberti, L. Mereu, A. Nanni - Corso di Matematica - Edizione mista
capitolo
2
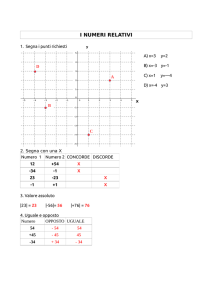
L’insieme dei numeri naturali e l’insieme degli interi L’insieme definito dai punti circolettati in
colore (fig. 1) rappresenta parte del grafico
G della relazione 7, pensato limitatamente all’insieme A = {0; 1; 2; …; 12}.
È interessante riconoscere alcune proprietà
geometriche:
12
11
10
9
8
7
A 6
• G contiene la diagonale e non potrebbe
essere diversamente, dal momento che la
relazione è riflessiva.
• G è simmetrico rispetto a tale diagonale:
infatti contiene il punto (2; 9) e il punto
(9; 2), contiene (5; 12) e (12; 5) ecc.
Questa è un’evidente conseguenza dell’essere la relazione simmetrica.
5
4
3
2
1
0
0
1 2 3 4 5 6 7 8 9 10 11 12
A
Figura 1
Classi resto modulo un intero
Consideriamo due numeri interi che divisi per 7 diano lo stesso resto, per esempio a = 39
e b = 25:
39 = 5 ⋅ 7 + 4
25 = 3 ⋅ 7 + 4
e
Allora la loro differenza
39 – 25 = 5 ⋅ 7 + 4 – (3 ⋅ 7 + 4) = 2 ⋅ 7
è multipla di 7, cioè 39 e 25 sono congrui modulo 7.
Viceversa, sappiamo che la divisione di a = 39 per 7 dà resto 4 e che b = 25 è congruo
ad a = 39 modulo 7 poiché la differenza a – b = 39 – 25 = 14 = 2 ⋅ 7 è un multiplo di 7.
Se ne deduce che
b = 25 = 39 – 14 = 5 ⋅ 7 + 4 – 2 ⋅ 7 = 3 ⋅ 7 + 4
cioè b = 25 nella divisione per 7 ha lo stesso resto di a = 39.
In generale, supponiamo che a e b siano due numeri interi che abbiano lo stesso resto nella divisione per m:
a = k 1m + r
b = k 2m + r
essendo 0 ≤ r < m
Sottraendo membro a membro si ha:
a – b = (k1 – k2)m = km
cioè i due numeri a e b sono congrui modulo m.
Viceversa supponiamo, dati i due numeri a e b interi, che
1. sia r il resto della divisione di a per m:
2. sia
2
a = qm + r
a ≡ b (mod m)
cioè
0≤r<m
a – b = km
© 2010 RCS Libri S.p.A., ETAS - L. Lamberti, L. Mereu, A. Nanni - Corso di Matematica - Edizione mista
capitolo
2
L’insieme dei numeri naturali e l’insieme degli interi Allora risulta:
b = a – km = qm + r – km = (q – k)m + r = hm + r
quindi a e b divisi per m hanno lo stesso resto.
Concludendo, vale il seguente
TEOREMA Affinché due interi relativi a e b siano congrui modulo m è necessario e suffi-
ciente che essi abbiano lo stesso resto nella divisione euclidea per m.
Considerata, ora, la relazione m di congruenza modulo un intero m ≥ 2 tra interi relativi, la classe di equivalenza [a] formata dagli interi congrui ad a modulo m, cioè dai numeri del tipo:
a + km
con k ∈
prende il nome di classe resto modulo m.
Gli elementi della classe [a] sono quindi i numeri interi che divisi per m danno lo stesso resto, uguale a quello della divisione di a per m.
L’insieme quoziente / m (vedi cap. 1 par. 9) è formato dalle m classi di equivalenza:
[0], [1], [2], …, [m − 1]
dove nella classe [0] ci sono tutti i numeri interi tali che il resto della divisione per m è uguale a zero, cioè i multipli di m, nella classe [1] tutti i numeri interi tali che il resto della divisione per m è uguale a 1, nella classe [2] tutti i numeri interi tali che il resto della divisione
per m è uguale a 2, …
Che dire della congruenza se m = 1? Tutti gli interi sono congrui tra loro modulo 1: l’unica
classe di equivalenza che si produce è la classe [0].
Come esempio riprendiamo in considerazione la relazione 7 definita in , considerata nell’esempio 1.
sempi
2
Sia 7 la relazione di equivalenza definita in , cioè:
a 7 b
⇔
∃k e a – b = 7k
Appartengono alla classe [a] tutti gli elementi b di tali che la differenza (a – b) sia multipla di 7. È chiaro che l’insieme quoziente / 7 è costituito dalle sette classi:
[0]; [1]; [2]; [3]; [4]; [5]; [6]
Ciascuna di esse è costituito da:
[0] = {0; ± 7; ± 14; ± 21; …}
[1] = {…; –13; –6; 1; 8; …}
[2] = {…; –12; –5; 2; 9; …}
[3] = {…; –11; –4; 3; 10; …}
…
[6] = {…; –8; –1; 6; 13; …}
Si osservi che ogni elemento di appartiene a una sola delle suddette classi, il cui elemento
rappresentativo non è altro che il resto della divisione tra il numero dato e 7.
3
© 2010 RCS Libri S.p.A., ETAS - L. Lamberti, L. Mereu, A. Nanni - Corso di Matematica - Edizione mista
capitolo
2
3
L’insieme dei numeri naturali e l’insieme degli interi Congruenza modulo m = 2
Se a e b sono numeri interi, diremo
a ≡ b (mod 2)
se la differenza (a – b) è divisibile per 2, cioè è multiplo di 2:
a – b = 2k
Abbiamo visto che due numeri sono congrui modulo 2 se divisi per 2 danno lo stesso resto e
poiché i possibili resti delle divisioni per 2 sono
0
e
1
l’insieme quoziente / 2 è costituito dalle sole due classi :
[0] = {0; ±2; ± 4; ± 6; …}
[1] = {…; – 5; – 3; –1; 1, 3, 5, …}
Nella classe [0] sono contenuti tutti i numeri pari, nella classe [1] tutti i numeri dispari.
Aritmetica delle classi resto
L’insieme quoziente / m, insieme delle classi resto modulo m, come abbiamo visto, è
costituito da m elementi, le classi:
[0], [1], [2], …, [m – 1]
individuate dai possibili resti della divisione per m dei numeri interi.
Indicheremo in generale con
[a] m
la classe di tutti gli interi congrui al numero a modulo m.
Sull’insieme delle classi resto si può “fare dell’aritmetica” con le seguenti definizioni di
somma e di prodotto:
Somma: [a]m + [b]m = [a + b]m
Prodotto: [a]m ⋅ [b]m = [a ⋅ b]m
sempio
4
Supponiamo di aver scelto m = 6; allora, per definizione:
[3]6 + [10]6 = [13]6
[5]6 ⋅ [8]6 = [40]6
Nell’“aritmetica” introdotta la classe [0]m ha, naturalmente, il ruolo dello zero nell’addizione e la classe [1]m quello dell’unità nella moltiplicazione.
La tabella a fianco esprime la somma delle
classi resto modulo 5.
La classe [b]m si dice opposta della classe
[a]m se:
[a]m + [b]m = [b]m + [a]m = [0]m
Nella tabella, per esempio, la classe [2]5 è
opposta alla classe [3]5 e viceversa.
4
+
[0]
[1]
[2]
[3]
[4]
[0]
[1]
[2]
[3]
[4]
[0]
[1]
[2]
[3]
[4]
[1]
[2]
[3]
[4]
[0]
[2]
[3]
[4]
[0]
[1]
[3]
[4]
[0]
[1]
[2]
[4]
[0]
[1]
[2]
[3]
© 2010 RCS Libri S.p.A., ETAS - L. Lamberti, L. Mereu, A. Nanni - Corso di Matematica - Edizione mista
capitolo
2
L’insieme dei numeri naturali e l’insieme degli interi La tabella a fianco costituisce, invece, la tabella
moltiplicativa delle classi resto modulo 5: si noti
che abbiamo trascurato, come nella tradizionale tavola pitagorica, le moltiplicazioni per la classe [0].
La classe [b]m ≠ [0]m si dice reciproca della
classe [a]m se:
[a]m ⋅ [b]m = [b]m ⋅ [a]m = [1]m
×
[1]
[2]
[3]
[4]
[1]
[2]
[3]
[4]
[1]
[2]
[3]
[4]
[2]
[4]
[1]
[3]
[3]
[1]
[4]
[2]
[4]
[3]
[2]
[1]
Nella tabella, per esempio, la reciproca della classe [4]5 è se stessa.
Prima osservazione
[3]6 = {…, 3, 9, 15, 21, …} = [9]6
[10]6 = {…, 4, 10, 16, 22, …} = [16]6
Riuscirà, secondo la nostra definizione, [3]6 + [10]6 = [9]6 + [16]6?
Per fortuna sì!
Infatti:
[9]6 + [16]6 = [25]6 = {…; 1; 7; 13; 19; 25; 31; …} = [13]6
Seconda osservazione
[3]6 ⋅ [2]6 = [6]6 = [0]6
Il prodotto di due classi diverse dalla classe zero dà la classe zero!
Nell’aritmetica delle classi resto può cadere la ben nota proprietà di annullamento del prodotto che coincide con l’annullamento di uno almeno dei fattori.
Si noti tuttavia che l’“incidente” emerso in relazione al prodotto nelle classi resto modulo 6 non può comparire in classi resto modulo un numero m primo.
Terza osservazione
Saper decidere se un numero b ∈[0]m equivale a saper decidere se b è divisibile per m.
Osservazione
Un criterio di divisibilità
Scritto il numero intero n in forma decimale come
n = … n 3n 2n 1n 0
cioè
n = n 0 + n 1 · 10 + n 2 ⋅ 10 2 + n 3 ⋅ 10 3 + …
si ha:
[n] 11 = [n 0] 11 + [n 1] 11 ⋅ [10] 11 + [n 2] 11 ⋅ [10 2] 11 + [n 3 ] 11 ⋅ [10 3] 11 + …
Le cifre n 3, n 2, n 1, n0 sono comprese tra 0 e 9, quindi non cambiano considerandole
“modulo 11”.
Poiché 10 ≡ −1 (mod 11) si ha del resto:
10 2 ≡ 1 (mod 11)
10 3 ≡ −1 (mod 11)
ecc.
Quindi: [n]11 = [n 0 − n1 + n 2 − n 3 + …], da cui [n]11 = [0]11, ovvero 11 è divisore di
n se e solo se la somma alternata delle cifre di n
n0 − n 1 + n 2 − n 3 + …
è un multiplo di 11.
Per esempio, il numero 88 è divisibile per 11 (ben noto!) ma lo è anche il numero
723 314 245 423
infatti:
5
3−2+4−5+4−2+4−1+3−3+2−7=0
© 2010 RCS Libri S.p.A., ETAS - L. Lamberti, L. Mereu, A. Nanni - Corso di Matematica - Edizione mista