RISOLUZIONE MODERNA DI PROBLEMI ANTICHI
“L’intelletto, dunque, che non è la verità, non comprende mai la verità in modo così preciso
da non poterla comprendere (poi ancora) più precisamente, all’infinito, perché sta alla
verità come il poligono sta al cerchio. Quanti più angoli avrà il poligono inscritto, tanto più
sarà simile al cerchio; tuttavia non sarà mai uguale ad esso, anche se avremo moltiplicato
i suoi angoli all’infinito, a meno che non si risolva con l’identità con il circolo.”
Nicola Cusano – La dotta ignoranza, I-IV
LA RISOLUZIONE MODERNA DELLA PROPOSIZIONE 1
Ogni cerchio è uguale ad un triangolo se ha il raggio uguale ad un cateto [del
triangolo] e la circonferenza uguale alla base [uguale all’altro cateto].
c
N
R
R
C
Il metodo di esaustione, secondo l’interpretazione moderna, consiste nel dimostrare che
due grandezze sono uguali perché è assurdo che la loro differenza abbia un valore
diverso da zero. Per fare ciò si mettono a confronto due classi di grandezze, dette
contigue. Ricordiamo che due classi di grandezze si dicono contigue quando:
-sono separate, ovvero ogni grandezza della prima classe è minore di ogni grandezza
della seconda;
-comunque si scelga una grandezza ε, omogenea alle grandezze date e piccola a piacere,
si possono sempre trovare una grandezza della prima classe e una della seconda in modo
che la loro differenza sia minore della grandezza ε;
-l’elemento separatore delle due classi, che è unico ed è la grandezza cercata.
Per determinare l’area di un cerchio si considerano perciò le due classi contigue costituite
dalle aree dei poligoni inscritti e circoscritti al cerchio stesso; si dimostra che l’area del
cerchio è l’elemento separatore di tali classi. Intuitivamente man mano che il numero dei
lati dei poligoni considerati aumenta, la loro area si avvicina sempre più all’area del
cerchio.
Per dimostrare che un cerchio è equivalente ad un triangolo che ha base congruente alla
circonferenza rettificata e altezza congruente al raggio, si considerano un cerchio di area
C e un triangolo di area E e due classi contigue costituite rispettivamente dalle aree dei
poligoni inscritti nel cerchio dato e dalle aree dei poligoni circoscritti al cerchio dato.
Si può dimostrare che ogni poligono regolare è equivalente ad un triangolo che ha la base
congruente al suo perimetro e l’altezza congruente alla sua apotema; da questo segue
che:
-poiché ogni poligono regolare inscritto nel cerchio ha un perimetro minore della
circonferenza rettificata e apotema minore del raggio, allora la sua area è minore di quella
del triangolo E;
-poiché ogni poligono regolare circoscritto al cerchio ha un perimetro maggiore della
circonferenza rettificata e apotema congruente al raggio, allora la sua area è maggiore di
quella del triangolo E;
-l’area E del triangolo è dunque l’elemento separatore delle due classi contigue
considerate; poichè anche l’area C del cerchio è elemento separatore delle stesse due
classi contigue ( e sappiamo che l’elemento separatore è unico), allora C=E.
RISOLUZIONE MODERNA DELLA PROPOSIZIONE 3
La circonferenza di ogni cerchio è tripla del diametro e lo supera ancora di meno di
un settimo del diametro, e di più di dieci settantunesimi.
Archimede per determinare la lunghezza della circonferenza e l’area del cerchio considera
di fatto la successione dei perimetri e rispettivamente delle aree dei poligoni inscritti e
circoscritti alla circonferenza data, utilizzando solo le conoscenze geometriche e
aritmetiche che si avevano ai tempi di Pitagora ed Euclide.
Oggi possiamo analizzare gli stessi problemi utilizzando le relazioni trigonometriche a noi
note e determinare la lunghezza della circonferenza come il valore del limite a cui tende
sia la successioni dei perimetri dei poligoni regolari di n lati inscritti che quella dei perimetri
dei poligoni regolari di n lati circoscritti alla circonferenza data, al crescere del numero n
dei lati.
Possiamo poi visualizzare l’approssimazione di pigreco, calcolata da Archimede, con
l’utilizzo di moderni programmi informatici come Excell.
Perimetro di un poligono inscritto
Consideriamo un poligono regolare di n lati
inscritto in una circonferenza di raggio
r=OA=OB. Sia AB un lato di tale poligono.
̂
Sia
l’angolo al centro della
circonferenza che insiste su AB.
L’angolo α può essere calcolato come
rapporto tra il valore dell’angolo di 360°
espresso in radianti, ossia , e il numero n
di lati della figura inscritta nella
circonferenza:
Calcoliamo quindi BH, ovvero la metà del
lato della figura regolare inscritta, usando il
Primo Teorema sui triangoli rettangoli:
Per calcolare il perimetro 2pn del poligono inscritto nella circonferenza, moltiplichiamo il
valore ottenuto per il numero n dei lati del poligono stesso:
Perimetro di un poligono circoscritto
Consideriamo ora il poligono regolare di n lati
circoscritto alla stessa circonferenza di raggio
r=OA=OB=OP. Sia CD un lato di tale poligono. Sia
̂
l’angolo al centro della circonferenza
individuato dai lati CO e OD.
L’angolo α risulta ancora dato da:
Calcoliamo DP, ovvero la metà del lato di tale
poligono applicando il Secondo Teorema sui
Triangoli rettangoli:
Calcoliamo infine il perimetro 2pn’ del poligono circoscritto alla circonferenza:
Osserviamo che pn e p’n approssimano rispettivamente per difetto e per eccesso la
lunghezza della circonferenza. Le due successioni, i cui termini generali sono dati da p n e
p’n, convergono allo stesso valore, che è proprio la lunghezza della circonferenza; infatti
se calcoliamo il limite a cui tendono i valori di tali perimetri all’aumentare del numero n dei
loro lati, si ottiene proprio la lunghezza della circonferenza C 2 r
sent
tgt
lim
1 )
(Nel fare i calcoli occorre ricordare il limite lim
t 0
t 0 t
t
lim p n lim 2nr sen
n
n
lim p' n lim 2nr tg
n
n
n
n
lim 2r
n
lim 2r
n
sen( / n)
2r
/n
tg ( / n)
2r
/n
Visualizziamo quanto trovato con Excell. In ascissa abbiamo il numero dei lati dei poligoni
inscritti e circoscritti ad una circonferenza di raggio r=1 e in ordinata i rispettivi perimetri
2pn e 2p’n
Numero
di lati n
Angolo α/2
in radianti
( )
6
7
8
9
…
153
154
155
0,523599
0,448799
0,392699
0,349066
…
0,020533
0,0204
0,020268
0,5
0,433884
0,382683
0,34202
…
0,020532
0,020399
0,020267
Lunghezza
dei lati
(
)
Perimetro 2pn
1
0,8677674782
0,7653668647
0,6840402867
…
0,041063685
0,040797075
0,040533904
6
6,074372348
6,122934918
6,15636258
…
6,282744
6,28275
6,282755
Perimetro poligoni inscritti
perimetro
6,3
6,25
6,2
6,15
6,1
6,05
6
n lati
5,95
0
20
40
60
Numero
di lati
Angolo
in radianti ( )
6
7
8
9
…
153
154
155
0,523599
0,448799
0,392699
0,349066
…
0,020533
0,0204
0,020268
80
0,57735
0,481575
0,414214
0,36397
…
0,020536
0,020403
0,020271
100
120
140
160
180
Lunghezza dei
lati (
)
Perimetro
2p’n
1,1547005384
0,9631492376
0,8284271247
0,7279404685
…
0,041072343
0,040805565
0,040542231
6,92820323
6,742044663
6,627416998
6,551464217
…
6,284068
6,284057
6,284046
Perimetro poligoni circoscritti
perimetro
7
6,9
6,8
6,7
6,6
6,5
6,4
6,3
6,2
0
50
100
150
200
n lati
Perimetri poligoni inscritti e circoscritti a confronto
perimetro
7
6,8
6,6
2p inscr
6,4
2p circ
6,2
6
n° lati
5,8
0
50
100
150
200
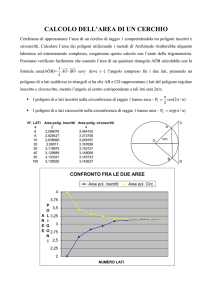
Analogamente possiamo determinare l’area di un cerchio come il valore del limite a cui
tende sia la successioni delle aree dei poligoni regolari di n lati inscritti sia quella delle
aree dei poligoni regolari di n lati circoscritti alla circonferenza data, al crescere del
numero n dei lati.
Possiamo anche in questo caso visualizzare l’approssimazione di pigreco, calcolata da
Archimede, con l’utilizzo di Excell.
Area di un poligono inscritto
Con riferimento alle figure precedenti, calcoliamo l’area del triangolo
come:
Moltiplicando tale area per il numero n dei lati si ottiene l’area S n del poligono regolare di n
lati inscritto nella circonferenza data:
Area di un poligono circoscritto
Con riferimento alle figure precedenti, calcoliamo l’area del triangolo COD come:
Moltiplicando tale area per il numero n dei lati si ottiene l’area S’ n del poligono regolare di
n lati inscritto nella circonferenza data:
Osserviamo che Sn e S’n approssimano rispettivamente per difetto e per eccesso l’area del
cerchio. Le due successioni, i cui termini generali sono dati da S n e S’n, convergono allo
stesso valore, che è proprio l’area del cerchio; infatti se calcoliamo il limite a cui tendono i
valori di tali aree all’aumentare del numero n dei loro lati, si ottiene proprio r 2
1 2
2
sen(2 / n)
nr sen
lim r 2
r 2
n 2
n
n
2 / n
lim S n lim
n
lim S ' n lim nr 2 tg
n
n
n
lim r 2
n
tg ( / n)
r 2
/n
Visualizziamo quanto trovato con Excell. In ascissa abbiamo il numero dei lati dei poligoni
inscritti e circoscritti ad una circonferenza di raggio r=1 e in ordinata le aree Sn e S’n.
Numero
lati n
Angolo α in
radianti ( )
6
7
8
9
1,0471975
0,8975979
0,7853981
0,6981317
…
1
0,867767478
0,765366865
0,684040287
…
0,433012702
0,390915741
0,353553391
0,321393805
…
2,59807621
2,73641019
2,82842712
2,89254424
...
0,0551156
0,0546363
0,0541653
0,055108685
0,054629599
0,054158769
0,02754388
0,027304608
0,027069454
3,14000234
3,14002987
3,1400567
…
114
115
116
Lunghezza
lato
Area (AOB)
Area totale
Sn=nS(AOB)
area
Area poligoni inscritti
3,2
3,1
3
2,9
2,8
2,7
2,6
n lati
2,5
0
20
Numero Angolo
lati
in
n
radianti
40
60
Area (COD)
80
100
Lunghezza
lato
(poligoni
circoscritti)
Area totale
Sn
(poligoni
inscritti)
0,577350269
0,481574619
0,414213562
0,363970234
...
1,154700538
0,963149238
0,828427125
0,727940469
...
3,46410162
3,37102233
3,3137085
3,27573211
...
2,598076211
2,736410189
2,828427125
2,892544244
...
0,0275578 0,027564809
0,0273181 0,027324995
0,0270826 0,027089319
0,055129617
0,054649989
0,054178637
3,14238817
3,14237439
3,14236097
3,14000234
3,140029874
3,140056698
0,523599
0,448799
0,392699
0,349066
…
...
114
115
116
140
Area totale
( )
6
7
8
9
120
Area poligoni circoscritti
perimetro
3,5
3,45
3,4
3,35
3,3
3,25
3,2
3,15
n lati
3,1
0
20
40
60
80
100
120
140
Area poligoni inscritti e circoscritti a confronto
area
3,5
3,4
3,3
3,2
area inscr
3,1
area circ
3
2,9
2,8
2,7
2,6
2,5
n lati
0
50
100
150
200
Nel 1767 J.H. Lambert è riuscito a dimostrare che è un numero irrazionale, cioè non può
essere scritto come quoziente tra due numeri interi. Solo nel 1882, F.Lindemann ha
dimostrato che è anche un numero trascendente, cioè non è soluzione di una equazione
polinomiale a coefficienti interi (come invece lo è ad esempio √ che è comunque un
numero irrazionale)