SIMULAZIONE PRIMO ESONERO (ES. DA SVOLGERE) DEL 28-03-2014
ESERCIZIO 1
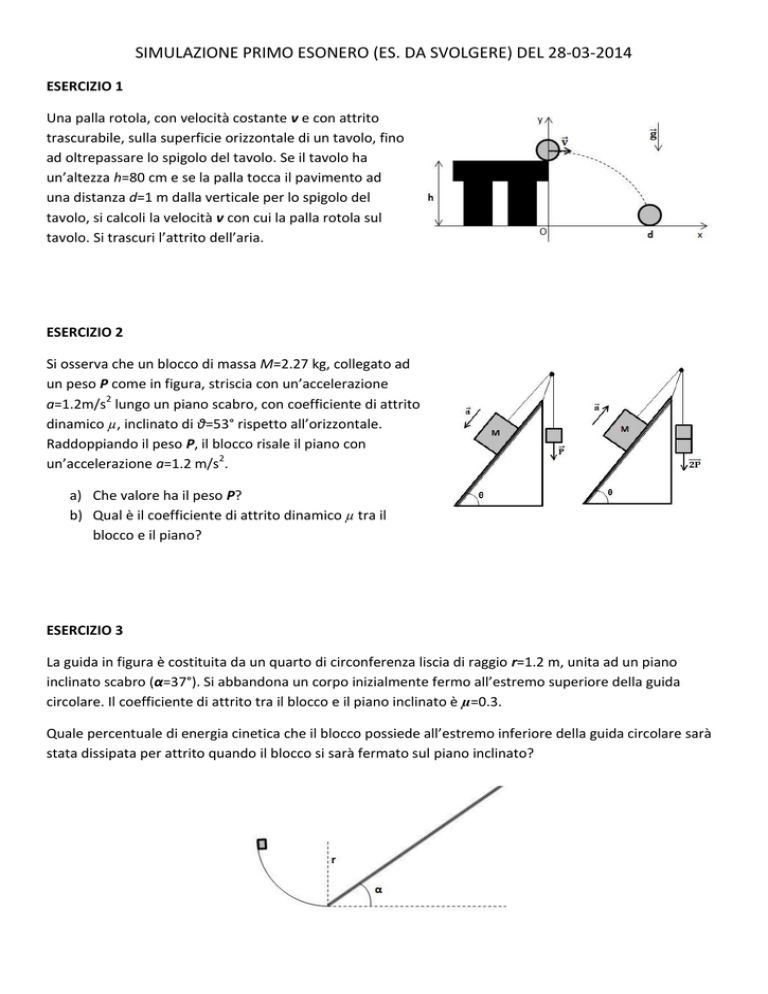
Una palla rotola, con velocità costante v e con attrito
trascurabile, sulla superficie orizzontale di un tavolo, fino
ad oltrepassare lo spigolo del tavolo. Se il tavolo ha
un’altezza h=80 cm e se la palla tocca il pavimento ad
una distanza d=1 m dalla verticale per lo spigolo del
tavolo, si calcoli la velocità v con cui la palla rotola sul
tavolo. Si trascuri l’attrito dell’aria.
ESERCIZIO 2
Si osserva che un blocco di massa M=2.27 kg, collegato ad
un peso P come in figura, striscia con un’accelerazione
a=1.2m/s2 lungo un piano scabro, con coefficiente di attrito
dinamico µ, inclinato di θ=53° rispetto all’orizzontale.
Raddoppiando il peso P, il blocco risale il piano con
un’accelerazione a=1.2 m/s2.
a) Che valore ha il peso P?
b) Qual è il coefficiente di attrito dinamico µ tra il
blocco e il piano?
ESERCIZIO 3
La guida in figura è costituita da un quarto di circonferenza liscia di raggio r=1.2 m, unita ad un piano
inclinato scabro (α=37°). Si abbandona un corpo inizialmente fermo all’estremo superiore della guida
circolare. Il coefficiente di attrito tra il blocco e il piano inclinato è µ=0.3.
Quale percentuale di energia cinetica che il blocco possiede all’estremo inferiore della guida circolare sarà
stata dissipata per attrito quando il blocco si sarà fermato sul piano inclinato?
ESERCIZIO 1
Una palla rotola, con velocità costante v e con attrito
trascurabile, sulla superficie orizzontale di un tavolo, fino
ad oltrepassare lo spigolo del tavolo. Se il tavolo ha
un’altezza h=80 cm e se la palla tocca il pavimento ad
una distanza d=1 m dalla verticale per lo spigolo del
tavolo, si calcoli la velocità v con cui la palla rotola sul
tavolo. Si trascuri l’attrito dell’aria.
SOLUZIONE
h=80 cm=0.8m
Dopo aver abbandonato l’estremità del tavolo, la palla compie un moto parabolico. In particolare, lungo l’asse
orizzontale x il moto è uniforme, mentre lungo y è uniformemente accelerato a causa dell’accelerazione di gravità.
Scriviamo le equazioni del moto proiettando sugli assi x e y:
x:
( )
y:
( )
Nel nostro caso:
Se chiamiamo t* il tempo impiegato dalla palla per toccare il pavimento una volta abbandonato il tavolo, le
equazioni del moto diventano:
( )
( )
Dalla seconda equazione ricaviamo t*:
√
Sostituendo t* nella prima equazione ricaviamo :
√
ESERCIZIO 2
Si osserva che un blocco di massa M=2.27 kg, collegato ad
un peso P come in figura, striscia con un’accelerazione
a=1.2m/s2 lungo un piano scabro, con coefficiente di attrito
dinamico µ, inclinato di θ=53° rispetto all’orizzontale.
Raddoppiando il peso P, il blocco risale il piano con
un’accelerazione a=1.2 m/s2.
a) Che valore ha il peso P?
b) Qual è il coefficiente di attrito dinamico µ tra il
blocco e il piano?
SOLUZIONE
Chiamiamo m la massa responsabile del peso P.
Scriviamo la II legge della dinamica per il sistema nel primo caso:
( )
CORPO M:
CORPO m:
Sommando membro a membro otteniamo:
( )
(
)
(*)
Scriviamo la II legge della dinamica per il sistema nel secondo caso:
( )
CORPO M:
CORPO 2m:
Sommando membro a membro otteniamo:
( )
(
)
(**)
Se sottraiamo la (**) alla (*) otteniamo:
( )
( )
P=mg=12.35 N
( )
Per trovare µ utilizziamo la (*):
da cui
( )
(
(
)
)
( )
con
( )
ESERCIZIO 3
La guida in figura è costituita da un quarto di circonferenza liscia di raggio r=1.2 m, unita ad un piano
inclinato scabro (α=37°). Si abbandona un corpo inizialmente fermo all’estremo superiore della guida
circolare. Il coefficiente di attrito tra il blocco e il piano inclinato è µ=0.3.
Quale percentuale di energia cinetica che il blocco possiede all’estremo inferiore della guida circolare sarà
stata dissipata per attrito quando il blocco si sarà fermato sul piano inclinato?
SOLUZIONE
Chiamiamo A l’istante in cui il corpo è in cima alla guida circolare (condizione iniziale), B l’istante in cui si trova
all’estremo inferiore della guida circolare e C l’istante in cui si ferma sul piano inclinato.
La guida circolare è liscia, per cui possiamo utilizzare il principio di conservazione dell’energia tra A e B:
Essendo il piano inclinato scabro, tra B e C dobbiamo utilizzare il teorema delle forze vive:
con
( )
( )
(
)
(
( )
( )
)
( )
La perdita di energia nel tratto Δl sarà quindi:
(
)
,
ovvero il 29%












